




次へ: 重力波の生成
上へ: インフレーション理論におけるゆらぎの生成
前へ: インフレーション理論と初期ゆらぎ
目次
索引
Subsections
インフラトンのふるまいを知るため,一般の曲がった時空中での実スカラー場
のゆらぎの運動を調べる必要がある.実スカラー場のラグランジアン密度は式
(B.2.81),すなわち
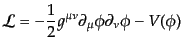 |
(K.2.1) |
で与えられる.このときの運動方程式は式(B.2.82),すなわち
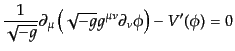 |
(K.2.2) |
となり,対称エネルギー運動量テンソルは式(B.2.84),すなわち
![$\displaystyle {T^\mu}_\nu = g^{\mu\lambda}\partial_\lambda \phi \partial_\nu \p...
...ac12 g^{\alpha\beta} \partial_\alpha \phi \partial_\beta \phi + V(\phi) \right]$](img3473.png) |
(K.2.3) |
である.このスカラー場のゆらぎを相対論的に扱うため,第10章の
相対論的摂動論の手法を適用する.まず,スカラー場を非摂動部と摂動部に分
け,
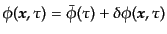 |
(K.2.4) |
とする.ここで,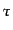 はコンフォーマル時間である.すると,運動方程式
(11.2.2)は非摂動部について
はコンフォーマル時間である.すると,運動方程式
(11.2.2)は非摂動部について
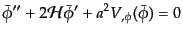 |
(K.2.5) |
また摂動部について
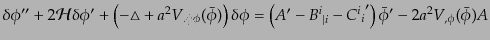 |
(K.2.6) |
と計算される.ここでダッシュはコンフォーマル時間での微分,また,
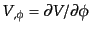 などの記号を使った.以降
などの記号を使った.以降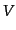 ,
,
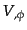 ,
,
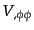 などは
などは
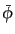 で評価される量として引数
を省略する.
で評価される量として引数
を省略する.
エネルギー運動量テンソル(11.2.3)の一様成分は
となるのでエネルギー密度と圧力の一様成分は
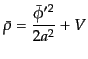 |
|
|
(K.2.10) |
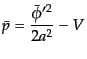 |
|
|
(K.2.11) |
と表される.さらに式(11.2.3)のゆらぎの成分は
| |
|
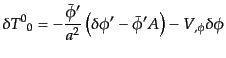 |
(K.2.12) |
| |
|
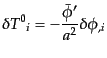 |
(K.2.13) |
| |
|
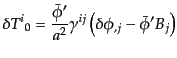 |
(K.2.14) |
| |
|
![$\displaystyle \delta {T^i}_j =
\left[
\frac{\bar{\phi}'}{a^2}\left(\delta\phi' - \bar{\phi}' A\right)
- V_{,\phi} \delta\phi
\right] {\delta^i}_j$](img3489.png) |
(K.2.15) |
と計算されるので,式(10.4.124)-(10.4.127)と比べることにより,
エネルギー密度のゆらぎ(
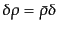 ),圧力のゆらぎ
),圧力のゆらぎ
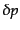 ,流速
,流速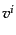 および非等方ストレス
および非等方ストレス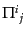 は
は
| |
|
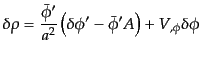 |
(K.2.16) |
| |
|
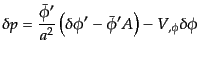 |
(K.2.17) |
| |
|
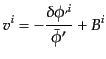 |
(K.2.18) |
| |
|
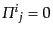 |
(K.2.19) |
と対応することがわかる.ここで,もし全物質ゲージなどの共動ゲージ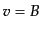 をとると式(11.2.17)によりスカラー場のゆらぎの非一様成分が消え
てしまうことに注意しよう.全物質ゲージは密度ゆらぎの成長を追うのには都
合がよいが,スカラー場のゆらぎがうまく取り扱えない.はじめからゲージ固
定をする方法では問題によって不適切なことが起こってしまう一例である.
をとると式(11.2.17)によりスカラー場のゆらぎの非一様成分が消え
てしまうことに注意しよう.全物質ゲージは密度ゆらぎの成長を追うのには都
合がよいが,スカラー場のゆらぎがうまく取り扱えない.はじめからゲージ固
定をする方法では問題によって不適切なことが起こってしまう一例である.
そこでスカラー場のゆらぎをゲージ不変な方法で取り扱う.スカラー場は座標
変換
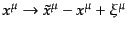 について不変,
つまり
について不変,
つまり
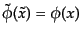 と変換するから,1次では
と変換するから,1次では
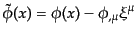 |
(K.2.20) |
となる.したがって,スカラー場ゆらぎのゲージ変換は
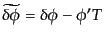 |
(K.2.21) |
で与えられる.すると次のようにゲージ不変なスカラー場ゆらぎが定義できる:
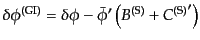 |
(K.2.22) |
そこで運動方程式(11.2.6)をこのゲージ不変量によって書き直すと当
然ゲージ依存項は消えて
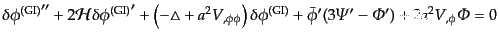 |
(K.2.23) |
となる.
また,式(10.4.145)-(10.4.147)のゲージ不変量は,式
(11.2.16)-(11.2.18)により
| |
|
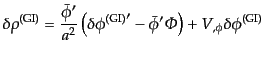 |
(K.2.24) |
| |
|
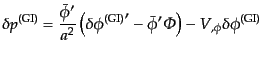 |
(K.2.25) |
| |
|
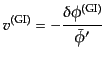 |
(K.2.26) |
と表される.
スカラー場の非等方ストレスがゼロになることから,アインシュ
タイン方程式(10.4.154)により計量のゲージ不変量について
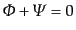 |
(K.2.27) |
となる.したがって運動方程式(11.2.23)は
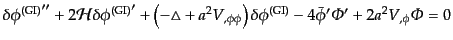 |
(K.2.28) |
と書き直せる.いまインフレーションにより平均曲率はほとんどゼロになって
いるので,簡単のため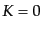 とおくことにする.この場合背景場の方程式
(10.4.82)は
とおくことにする.この場合背景場の方程式
(10.4.82)は
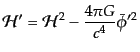 |
(K.2.29) |
となる.すると,非等方ストレスのない場合のアインシュタイン方程式
(10.4.174)-(10.4.176)はこの場合
| |
|
![$\displaystyle \triangle {\mit\Phi}- 3{\cal H} {\mit\Phi}' -
\left({\cal H}' +...
...\phi}' \delta{\phi^{\rm (GI)}}' +
a^2 V_{,\phi} \delta\phi^{\rm (GI)}
\right]$](img3508.png) |
(K.2.30) |
| |
|
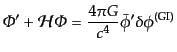 |
(K.2.31) |
| |
|
![$\displaystyle {\mit\Phi}'' + 3{\cal H}{\mit\Phi}' +
\left({\cal H}' + 2{\cal H...
...\phi}' \delta{\phi^{\rm (GI)}}' -
a^2 V_{,\phi} \delta\phi^{\rm (GI)}
\right]$](img3510.png) |
(K.2.32) |
となる.式(11.2.30)と式(11.2.32)を足した式
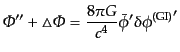 |
(K.2.33) |
と式(11.2.31)から
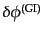 を消去すればゲージ不
変ポテンシャル
を消去すればゲージ不
変ポテンシャル
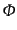 に対する方程式
に対する方程式
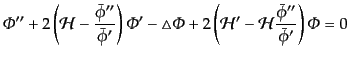 |
(K.2.34) |
を得る.
一方で,背景場の方程式(11.2.5)を用いると,スカラー場の音速に対
応する量は
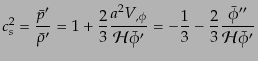 |
(K.2.35) |
と計算され,これを式(10.4.177)に用いれば
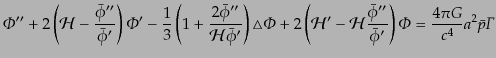 |
(K.2.36) |
となる.この式から式(11.2.34)を引けばエントロピーゆらぎが
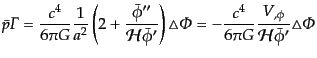 |
(K.2.37) |
で与えられることがわかる.
ここで次のゲージ不変な変数
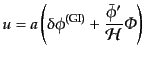 |
(K.2.38) |
を導入すれば式(11.2.34)はスカラー場の方程式(11.2.5),
(11.2.28)を用いることにより
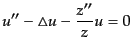 |
(K.2.39) |
となることがわかる.ここで
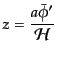 |
(K.2.40) |
は背景時空の時間変化によってきまる,時間のみの関数である.この変数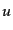 は式(10.5.197)の曲率ゆらぎ
は式(10.5.197)の曲率ゆらぎ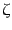 と密接な関係にある.事実,ゲー
ジ不変速度は式(11.2.26)で与えられるので,曲率ゆらぎは
と密接な関係にある.事実,ゲー
ジ不変速度は式(11.2.26)で与えられるので,曲率ゆらぎは
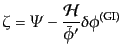 |
(K.2.41) |
となる.ここからただちに
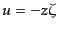 |
(K.2.42) |
であることがわかる.
運動方程式(11.2.38)は次の作用から導かれることがわかる:
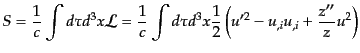 |
(K.2.43) |
ただしいまは平坦な背景時空を考えていることに注意する.ここではラグラン
ジアン密度を運動方程式から求めたが,実は,同じものを重力とスカラー場の
共存系の作用(式(B.2.78), (B.2.79), (B.2.81)を見よ)
![$\displaystyle S = \frac{1}{c}\int\sqrt{-g}d^4x \left[ \frac{c^4}{16\pi G}R - \frac12 g^{\mu\nu} \partial_\mu \phi \partial_\nu \phi - V(\phi) \right]$](img3525.png) |
(K.2.44) |
から直接導くことも可能である.この作用から計量とスカラー場について展開
して2次の摂動を取り出し,背景場の方程式を代入し,さらにゲージ変換に関
する拘束条件を求めて代入して,さらに表面項を落とせば導かれる
K1のだが,かなり長い計算を必要と
する.
式(11.2.40)のラグランジアン密度を静止時空上での自由スカラー場
のラグランジアン密度(8.4.101)と比較してみれば,質量項が
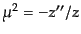 と対応し,有効的に質量が負で,さらに時間変化するような系と同等
なものであることがわかる.
と対応し,有効的に質量が負で,さらに時間変化するような系と同等
なものであることがわかる.
ここまでで重力場と(ミニマルに)結合した古典スカラー場がゲージ不変な形で
記述できたので,その量子化を行う.質量項の振る舞いを別にすれば得られた
ラグランジアンは本質的に平坦時空のスカラー場とほとんど変りはないので,
第8章で述べた場の量子化の手法をほぼ用いればよい.ただし,系
に時間並進不変性がないので、多少の拡張が必要である.いま、コンフォーマ
ル時間を時間変数にとるが、我々の定義ではコンフォーマル時間は長さの次元
をもっているので、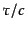 が適切な次元を持つ時間変数である。これに注意
して変数
が適切な次元を持つ時間変数である。これに注意
して変数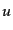 の共役運動量を求めると,
の共役運動量を求めると,
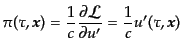 |
(K.2.45) |
となる.ここで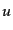 ,
, 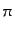 を場の演算子とみなし,場の量子化規則
を場の演算子とみなし,場の量子化規則
| |
|
![$\displaystyle \left[u(\tau,{\mbox{\boldmath$x$}}), u(\tau,{\mbox{\boldmath$y$}}...
...eft[\pi(\tau,{\mbox{\boldmath$x$}}), \pi(\tau,{\mbox{\boldmath$y$}})\right] = 0$](img3530.png) |
(K.2.46) |
| |
|
![$\displaystyle \left[u(\tau,{\mbox{\boldmath$x$}}), \pi(\tau,{\mbox{\boldmath$y$}})\right] =
i\hbar \delta^3({\mbox{\boldmath$x$}}-{\mbox{\boldmath$y$}})$](img3531.png) |
(K.2.47) |
を適用すればよい.場の演算子を平面波展開すると
![$\displaystyle u(\tau,{\mbox{\boldmath$x$}}) = \int \frac{d^3k}{(2\pi)^3 2 k} \l...
...i{\mbox{\scriptsize\boldmath$k$}}\cdot{\mbox{\scriptsize\boldmath$x$}}} \right]$](img3532.png) |
(K.2.48) |
となる.ここでいま系の時間並進対称性が失われているから,基本モードは
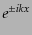 の形にはならず時間成分は関数
の形にはならず時間成分は関数 で与えられる.ここ
で
で与えられる.ここ
で
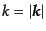 である.基本モードは運動方程式の解の完全系からつくら
れるから,この関数は微分方程式
である.基本モードは運動方程式の解の完全系からつくら
れるから,この関数は微分方程式
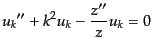 |
(K.2.49) |
の解として求められる.時刻一定面における場のスカラー積を
![$\displaystyle \left(\phi_1,\phi_2\right) = -i \int d^3x \left[ \phi_1(\tau,{\mb...
...mbox{\boldmath$x$}})}{\partial\tau}\phi_2^*(\tau,{\mbox{\boldmath$x$}}) \right]$](img3536.png) |
(K.2.50) |
で定義すると,基本モードはこのスカラー積について直交する.ここでモード
関数の時間成分はもはや時間微分の固有関数ではないが,次のロンスキアン
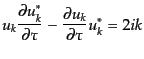 |
(K.2.51) |
で規格化すると,基本モードの規格直交性は次のようになる:
| |
|
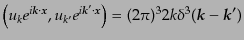 |
(K.2.52) |
| |
|
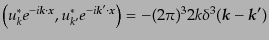 |
(K.2.53) |
| |
|
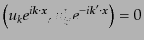 |
(K.2.54) |
したがって生成消滅演算子は基本モードの直交性から時刻によらずに
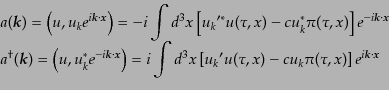 |
(K.2.55) |
を満たすから,どの時刻で量子化しようとも
![\begin{displaymath}\begin{array}{l} \left[ a({\mbox{\boldmath$k$}}), a^\dagger({...
...$}}), a^\dagger({\mbox{\boldmath$k$}}') \right] = 0 \end{array}\end{displaymath}](img1826.png) |
(K.2.56) |
という交換関係になる.こうしてあとは通常のように真空を
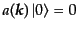 により定義して,ここから生成演算子によりフォック
空間を構成すればよい.
により定義して,ここから生成演算子によりフォック
空間を構成すればよい.
このように量子化されたゆらぎの場が式(11.2.48)で与えられることに
なる.インフレーション模型においてはインフレーション前に存在した古典的
なゆらぎは空間の急激な膨張によりならされて消えてしまっていて,唯一現在
に引き継がれるゆらぎは場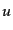 の真空中での量子ゆらぎのみであると通常仮定
される.ここで場
の真空中での量子ゆらぎのみであると通常仮定
される.ここで場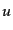 の空間的フーリエ変換
の空間的フーリエ変換
![$\displaystyle \widetilde{u}(\tau,{\mbox{\boldmath$k$}}) = \int d^3x e^{-i{\mbox...
...a({\mbox{\boldmath$k$}}) + u_k^*(\tau) a^\dagger({\mbox{\boldmath$k$}}) \right]$](img3543.png) |
(K.2.57) |
により,真空期待値から導かれるゆらぎの空間的パワースペクトル
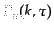 は
は
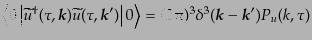 |
(K.2.58) |
により得られる.交換関係(11.2.56)を用いてこれを計算すれば,
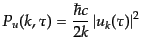 |
(K.2.59) |
という結果を得る.
こうして,モード関数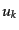 の時間的振る舞いが量子ゆらぎの振幅を決めてい
ることがわかる.モード関数は短いスケールにおいては通常の平坦静止空間の
場の理論におけるものに一致するはずである.事実,
の時間的振る舞いが量子ゆらぎの振幅を決めてい
ることがわかる.モード関数は短いスケールにおいては通常の平坦静止空間の
場の理論におけるものに一致するはずである.事実,
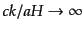 の極限では方程式(11.2.49)は
の極限では方程式(11.2.49)は
 となり,
規格化(11.2.51)を満たす解は
となり,
規格化(11.2.51)を満たす解は
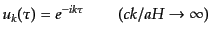 |
(K.2.60) |
で与えられる.一方,逆に長いスケールの極限
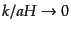 において
方程式(11.2.49)は
において
方程式(11.2.49)は
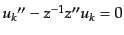 となりこれを積分
すると解として波数
となりこれを積分
すると解として波数 に依存する係数を別にすれば
に依存する係数を別にすれば
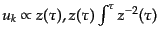 を得る.ここでインフレーション中,スロー
ロール近似が成り立つならばポテンシャルの傾き
を得る.ここでインフレーション中,スロー
ロール近似が成り立つならばポテンシャルの傾き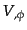 と膨張率
と膨張率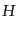 はあ
まり変化せず,式(5.3.40)から
はあ
まり変化せず,式(5.3.40)から
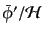 の変化も小さい
ので
の変化も小さい
ので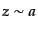 のような振る舞いをする.したがって成長する解は前者で,後
者は減衰する.成長解のみ取り出せば漸近的に
のような振る舞いをする.したがって成長する解は前者で,後
者は減衰する.成長解のみ取り出せば漸近的に
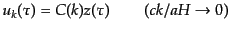 |
(K.2.61) |
の形となる.ここで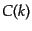 は初期条件から決まる関数であり,また減衰解を落
としてあるから,ロンスキアンの規格化は満たしていないがかまわない.この
場合,曲率ゆらぎ(11.2.41)のパワースペクトルは式
11.2.42)により
は初期条件から決まる関数であり,また減衰解を落
としてあるから,ロンスキアンの規格化は満たしていないがかまわない.この
場合,曲率ゆらぎ(11.2.41)のパワースペクトルは式
11.2.42)により
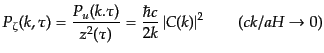 |
(K.2.62) |
となり,時間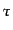 によらずに一定値をとる.このように,超ハッブルスケール
でスペクトルが時間変化しない曲率ゆらぎは便利な量である.その具体的なス
ペクトル形は漸近的な関数
によらずに一定値をとる.このように,超ハッブルスケール
でスペクトルが時間変化しない曲率ゆらぎは便利な量である.その具体的なス
ペクトル形は漸近的な関数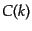 を求めることにより与えられる.以下,スロー
ロール近似の一次近似の範囲で求める.
を求めることにより与えられる.以下,スロー
ロール近似の一次近似の範囲で求める.
モード関数を完全に一般の場合に求めることはできないが,インフレーション
において必要なスローロール近似の下で近似的に求めることを考える.この場
合,ポテンシャルの形がいくつかの条件を満たす必要がある.このときに,ポ
テンシャルから導かれるパラメータで,スローロールに際して小さくなるよう
な量を求めておくと便利である.スローロール近似では式(5.3.38),
(5.3.39),すなわち
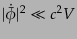 |
|
|
(K.2.63) |
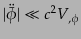 |
|
|
(K.2.64) |
を要請した.これにより,フリードマン方程式と場の運動方程式は
| |
|
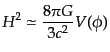 |
(K.2.65) |
| |
|
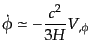 |
(K.2.66) |
と近似できるのであった.
条件(11.2.63), (11.2.64)をコンフォーマル時間の微分に
よって表せば
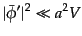 |
|
|
(K.2.67) |
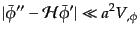 |
|
|
(K.2.68) |
となり,フリードマン方程式(10.4.72)と場の運動方程式
(11.2.5)は
| |
|
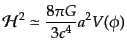 |
(K.2.69) |
| |
|
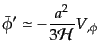 |
(K.2.70) |
と近似できる.
この最後の式(11.2.70)によりスローロールのはじめの条件
(11.2.67)からは
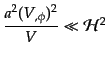 |
(K.2.71) |
が要請される.さらに式(11.2.70)とこれを微分したものを用いると
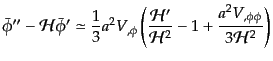 |
(K.2.72) |
となるが,式(11.2.33), (11.2.67)および式
(11.2.69)から
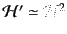 である.したがってス
ローロールの2番目の条件(11.2.68)からは
である.したがってス
ローロールの2番目の条件(11.2.68)からは
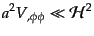 |
(K.2.73) |
が要請される.これらの式(11.2.71)と(11.2.73)に式
(11.2.69)を代入すれば,次のパラメータ
| |
|
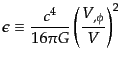 |
(K.2.74) |
| |
|
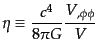 |
(K.2.75) |
が小さくなっていることがわかる.これらのパラメータをスローロールパラメー
タと呼び,スローロール近似が成り立つときには必ず小さくなっていなければ
ならない量である.
式(11.2.33), (11.2.70)および(11.2.73)を用いる
とこれらのスローロールパラメータはスローロール近似が成り立つ限り
| |
|
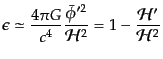 |
(K.2.76) |
| |
|
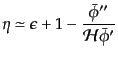 |
(K.2.77) |
とも表すことができる.ここで
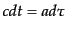 ,
,
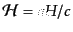 によりパ
ラメータ
によりパ
ラメータ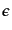 は
は
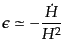 |
(K.2.78) |
と書ける.つまりパラメータ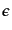 はハッブルパラメータが完全に一定
であるド・ジッター宇宙からのずれを表している.
はハッブルパラメータが完全に一定
であるド・ジッター宇宙からのずれを表している.
スローロールパラメータを用いて状態方程式の変数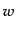 および音速
および音速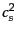 に
対応する量を1次まで求めてみると,(11.2.10),
(11.2.11), (11.2.35)から
に
対応する量を1次まで求めてみると,(11.2.10),
(11.2.11), (11.2.35)から
| |
|
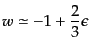 |
(K.2.79) |
| |
|
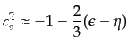 |
(K.2.80) |
が得られる.
スローロール近似ではポテンシャルは非常に平坦だからパラメータ
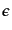 ,
, 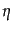 は時間的にほぼ一定にとどまる.そこでインフレーション
の間これらのパラメータは近似的に一定値をとると考えられる.このことを具
体的に見るため,スローロールパラメータの定義式を微分して,式
(11.2.69), (11.2.70)を用いると
は時間的にほぼ一定にとどまる.そこでインフレーション
の間これらのパラメータは近似的に一定値をとると考えられる.このことを具
体的に見るため,スローロールパラメータの定義式を微分して,式
(11.2.69), (11.2.70)を用いると
| |
|
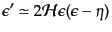 |
(K.2.81) |
| |
|
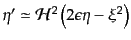 |
(K.2.82) |
が得られる.ここで新たなスローロールパラメータとして
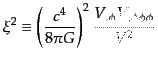 |
(K.2.83) |
を導入した.このパラメータはポテンシャルの微分を4回含んでいる.一方,
他のスローロールパラメータは微分を2回しか含んでいないので,他のパラメー
タの2次の量である.例えば
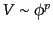 と表される場合を考えてみれば
と表される場合を考えてみれば
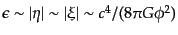 であることが
わかる.したがってスローロールパラメータ
であることが
わかる.したがってスローロールパラメータ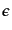 ,
, 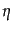 の時間微分は
スローロールパラメータの2次の量となり,1次近似では一定と考えられるこ
とを示している.
の時間微分は
スローロールパラメータの2次の量となり,1次近似では一定と考えられるこ
とを示している.
次に,スローロール近似の下,モード関数を求める微分方程式(11.2.49)
を解く.そのため,まず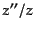 をスローロール近似において求める.式
(11.2.76), (11.2.77)からただちにスローロールの1次近
似で
をスローロール近似において求める.式
(11.2.76), (11.2.77)からただちにスローロールの1次近
似で
| |
|
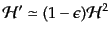 |
(K.2.84) |
| |
|
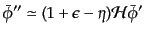 |
(K.2.85) |
がわかるが,これを用いて
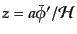 を微分すると同じく一
次近似で
を微分すると同じく一
次近似で
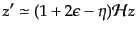 |
|
|
(K.2.86) |
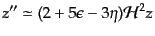 |
|
|
(K.2.87) |
であることがわかる.ここで2番目に式を導くのに,スローロールパラメータ
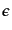 ,
, 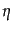 の微分は2次の量であることから落としてある.ここで式
(11.2.84)は,1次近似で
の微分は2次の量であることから落としてある.ここで式
(11.2.84)は,1次近似で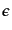 が一定であることから積分する
ことができ,関係式
が一定であることから積分する
ことができ,関係式
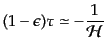 |
(K.2.88) |
を得る.ただし基準点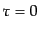 を無限の未来にとった.したがって式
(11.2.87)により
を無限の未来にとった.したがって式
(11.2.87)により
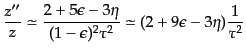 |
(K.2.89) |
と表される.ここで,
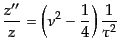 |
(K.2.90) |
とおくと便利であり,このとき は
は
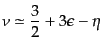 |
(K.2.91) |
となって,一次近似で一定値をとることがわかる.微分方程式
(11.2.49)はしたがって
![$\displaystyle \frac{d^2 u_k}{d\tau^2} + \left[k^2 - \left(\nu^2 - \frac14\right)\frac{1}{\tau^2}\right] u_k = 0$](img3596.png) |
(K.2.92) |
となる.ここで が一定であればこれはベッセル微分方程式であるから,
スローロールの一次近似の範囲内で一般解が求まることになる.その解は
が一定であればこれはベッセル微分方程式であるから,
スローロールの一次近似の範囲内で一般解が求まることになる.その解は
![$\displaystyle u_k(\tau) = \sqrt{\frac{\pi}{2}}\sqrt{-k\tau} \left[ \alpha_k H^{(1)}_\nu(-k\tau) + \beta_k H^{(2)}_\nu(-k\tau) \right]$](img3597.png) |
(K.2.93) |
で与えられ,ここで
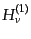 ,
,
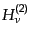 はそれぞれ第1種および第2
種ハンケル関数である.また
はそれぞれ第1種および第2
種ハンケル関数である.また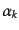 ,
, 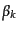 は積分定数であるが,規
格化(11.2.51)を満たすためには
は積分定数であるが,規
格化(11.2.51)を満たすためには
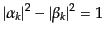 |
(K.2.94) |
であることが要請される.ここで積分定数を決定しない限りモード関数に不定
性があることに注意しよう.モード関数が決定しなければ真空(基底状態)も定
義できないことになる.一般に曲がった時空における真空の定義には不定性が
あり,観測者によって真空状態が異なって見えることに対応している.この不
定性は膨張のスケールよりもずっと小さい短波長極限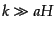 (
(
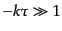 )において平坦なミンコフスキー時空における平面波解(11.2.57);
)において平坦なミンコフスキー時空における平面波解(11.2.57);
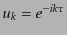 に一致するものを選ぶことにより除去される.このよう
に選ばれる真空をバンチ・デービス真空と呼ばれる.ハンケル関数の
に一致するものを選ぶことにより除去される.このよう
に選ばれる真空をバンチ・デービス真空と呼ばれる.ハンケル関数の
 における漸近形は
における漸近形は
![$\displaystyle H^{(1)}_\nu(x) \sim
\sqrt{\frac{2}{\pi x}}
\exp
\left[
i\left(x - \frac{\pi}{4} - \frac{\pi\nu}{2}\right)
\right]$](img3607.png) |
|
|
(K.2.95) |
![$\displaystyle H^{(2)}_\nu(x) \sim
\sqrt{\frac{2}{\pi x}}
\exp
\left[
-i\left(x - \frac{\pi}{4} - \frac{\pi\nu}{2}\right)
\right]$](img3608.png) |
|
|
(K.2.96) |
となるので,
![$ \alpha_k = \exp[i(\nu + 1/2)\pi/2]$](img3609.png) ,
,
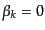 と
選べばよいことがわかる.したがって結局解は
と
選べばよいことがわかる.したがって結局解は
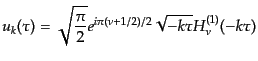 |
(K.2.97) |
で与えられることになる.
第一種ハンケル関数の
 における漸近形は
における漸近形は
 |
(K.2.98) |
であることから,解の長波長極限,つまり超ホライズンスケール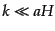 (
(
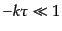 )における漸近形は
)における漸近形は
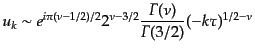 |
(K.2.99) |
で与えられる.ここでスローロールの最低次で
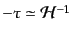 であること,および式(11.2.76)から導かれる
であること,および式(11.2.76)から導かれる
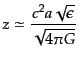 |
(K.2.100) |
を用いれば,式(11.2.61)の係数は
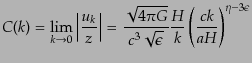 |
(K.2.101) |
となる.
上のようにスカラー場の量子ゆらぎは計算されるが,我々が観測する宇宙の構
造は古典ゆらぎであるからこの量子ゆらぎが古典ゆらぎと関係づけられる必要
がある.このスカラー場の量子ゆらぎがどこかで古典ゆらぎに転化するものと
考えられるが,一般に量子論において量子的状態が古典的状態に転化する機構
は理論的に最も不明瞭な部分である.通常の量子論では観測行為に対して確率
解釈が採用されて,物理量の古典化について詳細な機構を論じることなしに観
測量に対する理論的予言がなされるように構成されている.現在の宇宙におい
てゆらぎは古典的に振る舞っていると考えられるので,インフレーションの終
りには量子ゆらぎは古典化していると考えられる.だが,この場合には観測行
為が行われることなしにゆらぎが古典的にならねばならない.この点について,
通常インフレーション模型においてはハッブル半径に対応する長さよりも短い
スケールに発生する量子ゆらぎが,インフレーションによる膨張によってハッ
ブル半径よりも長いスケールのゆらぎとなることによりゆらぎが凍り付いて古
典的に振る舞うようになると仮定する.するとその古典化したゆらぎが曲率ゆ
らぎ(11.2.41)を導き,インフレーションが終わるとこれが再びハッ
ブル半径の中に入ってくることにより最終的に我々が観測する密度ゆらぎとな
るK2.
第10.6節で見たように,エントロピーゆらぎや非等方ストレスが密度
ゆらぎと同程度のオーダーである場合にはハッブル半径より長いスケールの曲
率ゆらぎは時間的に一定に保たれる.したがってインフレーションにより生成
された曲率ゆらぎはインフレーション終了後,再びハッブル半径の中に入って
くるまで振幅が変化しない.式(11.2.70)と(11.2.101)により
ハッブル半径を超えるスケールにおける曲率ゆらぎのパワースペクトルは
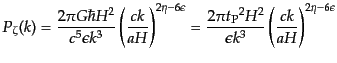 |
(K.2.102) |
となる。ここで、
 はプランク時間である。
あるいは無次元化されたスペクトル
はプランク時間である。
あるいは無次元化されたスペクトル
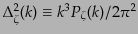 で表せば
で表せば
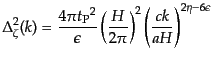 |
(K.2.103) |
となる.これを見ると,スローロールの最低次では 依存性が消えることが
わかる.こうして,スローロールの最低次では無次元スペクトル
依存性が消えることが
わかる.こうして,スローロールの最低次では無次元スペクトル
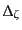 には
には 依存性のない,スケール不変なスペクトル
(scale-invariant spectrum)が生成される,という重要な結論が導き出され
る.また,スローロールパラメータの一次近似においてスケール不変性は破れ
ている.スカラーゆらぎのスペクトル指数
依存性のない,スケール不変なスペクトル
(scale-invariant spectrum)が生成される,という重要な結論が導き出され
る.また,スローロールパラメータの一次近似においてスケール不変性は破れ
ている.スカラーゆらぎのスペクトル指数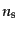 は
は 依存性により
依存性により
 で定義され,
で定義され,
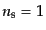 が
スケール不変なスペクトルに対応する.するとスローロールの一次近似におい
てスペクトル指数は
が
スケール不変なスペクトルに対応する.するとスローロールの一次近似におい
てスペクトル指数は
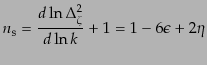 |
(K.2.104) |
となる.
インフレーションにより生成された非等方ストレスが無視できるものとすると,
曲率ゆらぎは
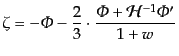 |
(K.2.105) |
で与えられる.これはエントロピーゆらぎが密度ゆらぎに比べて大きすぎない
限り,超ハッブルスケールで成長しない.古典化したエントロピーゆらぎは式
(11.2.37)から計算できるが,これは式(11.2.69),
(11.2.70)によりスローロール近似の最低次で
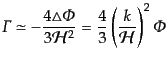 |
(K.2.106) |
となっている.ここで,最後の等式では波数 のゆらぎのモードを考えてい
る.したがって,超ハッブルスケール
のゆらぎのモードを考えてい
る.したがって,超ハッブルスケール
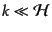 (
(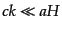 )にはエン
トロピーゆらぎは生成されないことがわかる.現在我々が観測する宇宙のゆら
ぎのスケールはインフレーション中にいったんハッブルスケールの外に出てい
たのであるから,インフレーションにより生成されるゆらぎはエントロピーゆ
らぎのない,断熱ゆらぎとなるK3.こうして,節10.6の議
論により,インフレーション終了後,曲率ゆらぎは超ハッブルスケールにおい
て時間的に一定に留まることになる:
)にはエン
トロピーゆらぎは生成されないことがわかる.現在我々が観測する宇宙のゆら
ぎのスケールはインフレーション中にいったんハッブルスケールの外に出てい
たのであるから,インフレーションにより生成されるゆらぎはエントロピーゆ
らぎのない,断熱ゆらぎとなるK3.こうして,節10.6の議
論により,インフレーション終了後,曲率ゆらぎは超ハッブルスケールにおい
て時間的に一定に留まることになる:
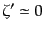 |
(K.2.107) |
この方程式はより直接的に導くこともできる.非等方ストレスのないときのポ
テンシャルの成長の一般式(10.4.177)においてエントロピーゆらぎをゼ
ロにおいたものに等価であることが確かめられる.
ゲージ不変ポテンシャル
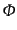 は超ハッブルスケールにおいても成長するの
で,インフレーション後に生成されてハッブルスケール内に入ってくるポテン
シャルのパワースペクトル
は超ハッブルスケールにおいても成長するの
で,インフレーション後に生成されてハッブルスケール内に入ってくるポテン
シャルのパワースペクトル
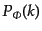 を求めるためには宇宙の状態方程式を
指定してゆらぎの成長を求める必要がある.次章で示すように,輻射優勢期
(RD)および物質優勢期(MD)には超ハッブルスケールのポテンシャルは成長しな
い.このような場合には曲率ゆらぎとポテンシャルの関係(11.2.105)は
単純に
を求めるためには宇宙の状態方程式を
指定してゆらぎの成長を求める必要がある.次章で示すように,輻射優勢期
(RD)および物質優勢期(MD)には超ハッブルスケールのポテンシャルは成長しな
い.このような場合には曲率ゆらぎとポテンシャルの関係(11.2.105)は
単純に
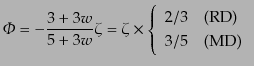 |
(K.2.108) |
となる.曲率ゆらぎは輻射優勢だろうが物質優勢だろうが時間的に一定である
から輻射優勢期にハッブル半径内に入ってくるポテンシャルの振幅と物質優勢
期に入ってくるそれとは,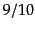 倍だけ後者の方が小さい.こうして結局イン
フレーションにより生成されたポテンシャルの(無次元化された)パワースペク
トルは輻射優勢期,物質優勢期での漸近的な形として
倍だけ後者の方が小さい.こうして結局イン
フレーションにより生成されたポテンシャルの(無次元化された)パワースペク
トルは輻射優勢期,物質優勢期での漸近的な形として
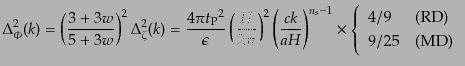 |
(K.2.109) |
となる.
Footnotes
- ...
する拘束条件を求めて代入して,さらに表面項を落とせば導かれるK1
- V. F. Mukhanov, H. A. Feldman, and R. H. Brandenberger,
Physics Report, Vol.215, 203-335 (1992)
- ...
るK2
- だが,あくまでインフレーション理論による初期ゆらぎの生成に
は量子状態の古典化という(正当化の明らかでない)仮定に基づいていることを
忘れてはならない.
- ...
らぎのない,断熱ゆらぎとなるK3
- この結論はインフラトン場が一種類
のみであることの帰結であり,多種類のインフラトン場を導入すればエントロ
ピーゆらぎを生成することも可能である.





次へ: 重力波の生成
上へ: インフレーション理論におけるゆらぎの生成
前へ: インフレーション理論と初期ゆらぎ
目次
索引
All rights reserved © T.Matsubara 2004-2010
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11
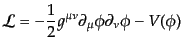
![]() について不変,
つまり
について不変,
つまり
![]() と変換するから,1次では
と変換するから,1次では
![]() と対応し,有効的に質量が負で,さらに時間変化するような系と同等
なものであることがわかる.
と対応し,有効的に質量が負で,さらに時間変化するような系と同等
なものであることがわかる.
![]() が適切な次元を持つ時間変数である。これに注意
して変数
が適切な次元を持つ時間変数である。これに注意
して変数![]() の共役運動量を求めると,
の共役運動量を求めると,
![]() の真空中での量子ゆらぎのみであると通常仮定
される.ここで場
の真空中での量子ゆらぎのみであると通常仮定
される.ここで場![]() の空間的フーリエ変換
の空間的フーリエ変換
![]() の時間的振る舞いが量子ゆらぎの振幅を決めてい
ることがわかる.モード関数は短いスケールにおいては通常の平坦静止空間の
場の理論におけるものに一致するはずである.事実,
の時間的振る舞いが量子ゆらぎの振幅を決めてい
ることがわかる.モード関数は短いスケールにおいては通常の平坦静止空間の
場の理論におけるものに一致するはずである.事実,
![]() の極限では方程式(11.2.49)は
の極限では方程式(11.2.49)は
![]() となり,
規格化(11.2.51)を満たす解は
となり,
規格化(11.2.51)を満たす解は
![]() および音速
および音速![]() に
対応する量を1次まで求めてみると,(11.2.10),
(11.2.11), (11.2.35)から
に
対応する量を1次まで求めてみると,(11.2.10),
(11.2.11), (11.2.35)から
![]() ,
, ![]() は時間的にほぼ一定にとどまる.そこでインフレーション
の間これらのパラメータは近似的に一定値をとると考えられる.このことを具
体的に見るため,スローロールパラメータの定義式を微分して,式
(11.2.69), (11.2.70)を用いると
は時間的にほぼ一定にとどまる.そこでインフレーション
の間これらのパラメータは近似的に一定値をとると考えられる.このことを具
体的に見るため,スローロールパラメータの定義式を微分して,式
(11.2.69), (11.2.70)を用いると
![]() をスローロール近似において求める.式
(11.2.76), (11.2.77)からただちにスローロールの1次近
似で
をスローロール近似において求める.式
(11.2.76), (11.2.77)からただちにスローロールの1次近
似で
![]() における漸近形は
における漸近形は
![]() は超ハッブルスケールにおいても成長するの
で,インフレーション後に生成されてハッブルスケール内に入ってくるポテン
シャルのパワースペクトル
は超ハッブルスケールにおいても成長するの
で,インフレーション後に生成されてハッブルスケール内に入ってくるポテン
シャルのパワースペクトル
![]() を求めるためには宇宙の状態方程式を
指定してゆらぎの成長を求める必要がある.次章で示すように,輻射優勢期
(RD)および物質優勢期(MD)には超ハッブルスケールのポテンシャルは成長しな
い.このような場合には曲率ゆらぎとポテンシャルの関係(11.2.105)は
単純に
を求めるためには宇宙の状態方程式を
指定してゆらぎの成長を求める必要がある.次章で示すように,輻射優勢期
(RD)および物質優勢期(MD)には超ハッブルスケールのポテンシャルは成長しな
い.このような場合には曲率ゆらぎとポテンシャルの関係(11.2.105)は
単純に
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11