




次へ: 曲率ゆらぎ
上へ: 相対論的摂動論
前へ: ゲージ不変量によるアインシュタイン方程式
目次
索引
Subsections
上に導いた式はゲージに全くよらずに成り立つ式である.したがって,ゲージ
固定について悩む必要はないのだが,実際にはゲージを固定する方法もよく行
われている.問題によっては特別なゲージ固定をすることにより計算が簡明に
なることがあるからである.そこで,とくによく使われるゲージ固定をいくつ
か取り上げて,ここまでのゲージ不変摂動論との関係を見ておこう.テンソル
型,およびベクトル型の摂動についてはほとんど明らかなので,ここではスカ
ラー型の摂動のみを考える.そして,特に断らないかぎりスカラー成分をあら
わす(S)の記号は省略する.
コンフォーマル・ニュートンゲージ(conformal Newtonian gauge)とは,縦型
ゲージ(longitudinal gauge)とも呼ばれ,摂動計量について条件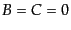 で定
義されるゲージ固定である.この場合,計量のゲージ不変量は
で定
義されるゲージ固定である.この場合,計量のゲージ不変量は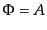 ,
,
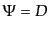 となることがわかるので,線素は
となることがわかるので,線素は
![$\displaystyle ds^2 = a^2(\tau) \left[-(1+2\Phi)d\tau^2 + (1+2\Psi)\gamma_{ij} dx^i dx^j\right]$](img3246.png) |
(J.5.177) |
で与えられる.この座標のもとでは,物質の膨張が等方的になっている.また,
物質に関するゲージ不変量
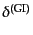 ,
,
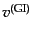 ,
,
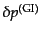 は,このゲージでの密度ゆらぎ,速度,圧力のゆらぎに等しく
なっている.つまり,これらのゲージ不変量はコンフォーマル・ニュートンゲー
ジにおけるそれぞれの物理量に対応していることがわかる.したがって,この
ゲージにおけるアインシュタイン方程式は式
(10.4.157)-(10.4.160)と全く同じ形である.
は,このゲージでの密度ゆらぎ,速度,圧力のゆらぎに等しく
なっている.つまり,これらのゲージ不変量はコンフォーマル・ニュートンゲー
ジにおけるそれぞれの物理量に対応していることがわかる.したがって,この
ゲージにおけるアインシュタイン方程式は式
(10.4.157)-(10.4.160)と全く同じ形である.
同期ゲージ(synchronous gauge)は解析表式が簡単化するためよく使われるも
のであるが,同時にゲージモードが紛れ込みやすいことでも知られている.こ
のゲージは次の線素で定義される.
![$\displaystyle ds^2 = a^2(\tau) \left[-d\tau^2 + \left(\gamma_{ij} + h_{ij}\right) dx^i dx^j\right]$](img3249.png) |
(J.5.178) |
このゲージでは隣り合った時間一定面の時間座標の間隔がその面に垂直方向に
計ったプロパーな時間に一致する.そしてまた空間座標が一定の線は時間一定
面に垂直となるように取ってある.通常,同期ゲージにおいては,計量の摂動
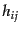 をトレース部
をトレース部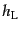 とゼロトレース部
とゼロトレース部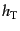 に分解する
ことが多い.スカラー成分について,この分解は次のようになる:
に分解する
ことが多い.スカラー成分について,この分解は次のようになる:
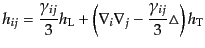 |
(J.5.179) |
すなわち,上の一般論において,
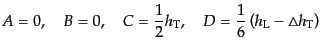 |
(J.5.180) |
とおいたものとなっている.このゲージ条件は実は座標を一意的に定めない.
すなわち,まだゲージ自由度が残っているのである.これを見るには,計量が
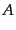 と
と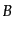 で表されるある与えられた座標からゲージ変換
(10.3.56)-(10.3.59) により
で表されるある与えられた座標からゲージ変換
(10.3.56)-(10.3.59) により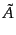 と
と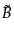 を消す
ための条件
を消す
ための条件
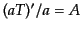 ,
,
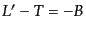 を考える.この条件を解けば,
を考える.この条件を解けば,
のように積分定数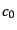 ,
, 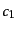 が含まれて,その分だけ同期ゲージには任意性
があることになる.この余計な自由度は運動方程式の段階で固定されていない
ので,初期条件により固定することになる.これを注意深く扱わないとゲージ
モードが紛れ込むことになる.
が含まれて,その分だけ同期ゲージには任意性
があることになる.この余計な自由度は運動方程式の段階で固定されていない
ので,初期条件により固定することになる.これを注意深く扱わないとゲージ
モードが紛れ込むことになる.
ゲージ不変量はこのゲージで,
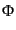 |
 |
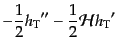 |
(J.5.183) |
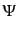 |
 |
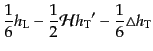 |
(J.5.184) |
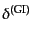 |
 |
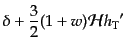 |
(J.5.185) |
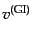 |
 |
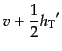 |
(J.5.186) |
と表されるので,運動方程式(10.4.157)-(10.4.158)は次の形にな
る:
| |
|
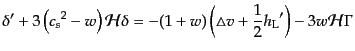 |
(J.5.187) |
| |
|
![$\displaystyle v' + \left(1 - 3 {c_s}^2\right){\cal H}v
= - \frac{{c_s}^2}{1+w}...
...
- \frac{w}{1+w}
\left[\Gamma + \frac23 \left(\triangle + 3K\right)\Pi\right]$](img3272.png) |
(J.5.188) |
また,拘束の式(10.4.159)-(10.4.160)は
| |
|
![$\displaystyle (\triangle + 3K)
\left[h_{\rm L} - \triangle h_{\rm T}
- 3{\cal...
...\right]
= -24\pi G a^2 \overline{\rho}
\left[\delta - 3(1+w) {\cal H}v\right]$](img3273.png) |
(J.5.189) |
| |
|
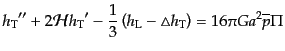 |
(J.5.190) |
となるが,この2つの式から
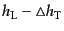 を消去する
と
を消去する
と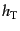 に関する時間発展方程式
に関する時間発展方程式
![$\displaystyle (\triangle + 3K) \left({h_{\rm T}}'' + {\cal H}{h_{\rm T}}'\right...
...\overline{\rho} \left[ \delta - 3(1+w){\cal H}v - 2w(\triangle + 3K)\Pi \right]$](img3276.png) |
(J.5.191) |
が得られる.さらにここで,式(10.4.152)を同期ゲージで書けば,
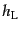 と
と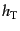 を結び付ける次のシンプルな関係が得られる:
を結び付ける次のシンプルな関係が得られる:
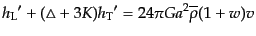 |
(J.5.192) |
そこでこれを用いて式(10.5.192)の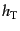 を消去すれば,
を消去すれば,
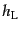 についての時間発展方程式
についての時間発展方程式
![$\displaystyle {h_{\rm L}}'' + {\cal H}{h_{\rm L}}' = - 8\pi G a^2 \overline{\rho} \left[ \left(1 + 3{c_s}^2\right) \delta + 3 w \Gamma \right]$](img3278.png) |
(J.5.193) |
が得られる.式(10.5.188), (10.5.189), (10.5.194)
は変数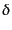 ,
, 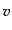 ,
, 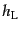 について方程式が閉じている.その解を用
いれば,式(10.5.193)あるいは式(10.5.192)により
について方程式が閉じている.その解を用
いれば,式(10.5.193)あるいは式(10.5.192)により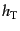 も求まることになる.この連立微分方程式は,時間について事実上4階と
なっている.すなわち,初期条件が4つ必要である.そのうち2つはこれまで
の考察からわかるようにゲージ自由度を固定するために必要なものである.
も求まることになる.この連立微分方程式は,時間について事実上4階と
なっている.すなわち,初期条件が4つ必要である.そのうち2つはこれまで
の考察からわかるようにゲージ自由度を固定するために必要なものである.
共動ゲージ(comoving gauge)では,全ての物質の平均速度に対する静止系によ
り時間一定面を定義する.これは
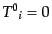 , すなわち,
, すなわち,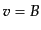 という条
件を課すことに等しい.さらに条件
という条
件を課すことに等しい.さらに条件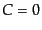 を加えればゲージは完全に固定され
る.このゲージでは時間一定面が必ず物質の4元速度と垂直になり,また空間
的なゆらぎの非等方成分が消え,等方成分のみとなっている.ここで残りの自
由度を
を加えればゲージは完全に固定され
る.このゲージでは時間一定面が必ず物質の4元速度と垂直になり,また空間
的なゆらぎの非等方成分が消え,等方成分のみとなっている.ここで残りの自
由度を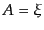 ,
, 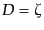 とおけばその線素は
とおけばその線素は
![$\displaystyle ds^2 = a^2(\tau) \left[ -(1 + 2\xi) d\tau^2 - 2 v_{\vert i} d\tau dx^i + \gamma_{ij}(1 + 2 \zeta) dx^i dx^j \right]$](img3284.png) |
(J.5.194) |
という形である.このゲージでは密度ゆらぎ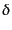 が式(10.4.164)で与
えられたバーディーンの変数
が式(10.4.164)で与
えられたバーディーンの変数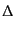 に一致し,速度も式(10.4.165のゲー
ジ不変な速度
に一致し,速度も式(10.4.165のゲー
ジ不変な速度
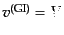 に一致する.他の変数はゲージ不変ポテン
シャルと
に一致する.他の変数はゲージ不変ポテン
シャルと
| |
|
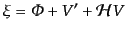 |
(J.5.195) |
| |
|
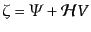 |
(J.5.196) |
の関係にある.したがって,このゲージでのアインシュタイン方程式は式
(10.4.166)-(10.4.169)のポテンシャルをこれらの変数で表し直し
たものとなる.バーディーン変数によるゆらぎに最も近いゲージであると言え
る.





次へ: 曲率ゆらぎ
上へ: 相対論的摂動論
前へ: ゲージ不変量によるアインシュタイン方程式
目次
索引
All rights reserved © T.Matsubara 2004-2010
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11
![]() で定
義されるゲージ固定である.この場合,計量のゲージ不変量は
で定
義されるゲージ固定である.この場合,計量のゲージ不変量は![]() ,
,
![]() となることがわかるので,線素は
となることがわかるので,線素は
![]() , すなわち,
, すなわち,![]() という条
件を課すことに等しい.さらに条件
という条
件を課すことに等しい.さらに条件![]() を加えればゲージは完全に固定され
る.このゲージでは時間一定面が必ず物質の4元速度と垂直になり,また空間
的なゆらぎの非等方成分が消え,等方成分のみとなっている.ここで残りの自
由度を
を加えればゲージは完全に固定され
る.このゲージでは時間一定面が必ず物質の4元速度と垂直になり,また空間
的なゆらぎの非等方成分が消え,等方成分のみとなっている.ここで残りの自
由度を![]() ,
, ![]() とおけばその線素は
とおけばその線素は
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11