




次へ: ゲージ不変量によるアインシュタイン方程式
上へ: 相対論的摂動論
前へ: 計量およびアインシュタインテンソルの摂動
目次
索引
さて、ここでゲージ自由度がどのように上の式に含まれているか調べておこう.
前に述べたように,一様な非摂動時空の各点を摂動時空の各点に一対一に対応
させる自由度がゲージ自由度であり,今の場合,摂動時空と非摂動時空の双方
の座標値が一致する点を対応させている.したがって,摂動時空の座標変換
を行えばこの対応関係が変更され,ゲージ変換をしたことになる.
そこで、座標変換
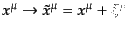 を
考える。ここで
を
考える。ここで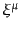 は計量の摂動と同じオーダーの微小量とする。この
とき計量の変換は
は計量の摂動と同じオーダーの微小量とする。この
とき計量の変換は
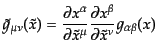 |
(J.3.42) |
となる。これを同一の座標値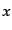 を持つ点で比べることにより,一次までのオー
ダーで
を持つ点で比べることにより,一次までのオー
ダーで
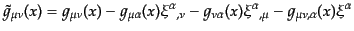 |
(J.3.43) |
というリー微分で表される.ゲージ変換では背景時空の座標が双方の座標で固
定されているので,この変換は摂動部分にのみ作用し、
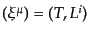 と書けば、
と書けば、
| |
|
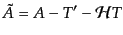 |
(J.3.44) |
| |
|
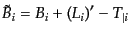 |
(J.3.45) |
| |
|
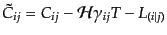 |
(J.3.46) |
と書き直せる。ここで、以前のように3次元背景空間の計量
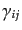 に
より添字の上げ下げおよび共変微分を定義している。
に
より添字の上げ下げおよび共変微分を定義している。
このように、計量を直接用いるとゲージ自由度が複雑に混在しているので、こ
のままでは扱いにくい。ところが、次に述べるように、摂動をテンソルの型に
従って分解すると扱いやすくなる。
摂動計量のうち、ベクトル量である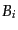 やテンソル量である
やテンソル量である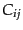 は、こ
のまま扱うよりも、スカラー型、ベクトル型、テンソル型に分解すると扱いや
すくなる.まず、ベクトル量である
は、こ
のまま扱うよりも、スカラー型、ベクトル型、テンソル型に分解すると扱いや
すくなる.まず、ベクトル量である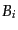 はあるスカラー場
はあるスカラー場
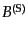 から
生成できる成分とその他の成分に分解して、
から
生成できる成分とその他の成分に分解して、
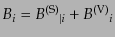 |
(J.3.47) |
とする。ここで、
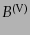 からはスカラーを作ることができない,すな
わち,発散がゼロ
からはスカラーを作ることができない,すな
わち,発散がゼロ
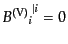 |
(J.3.48) |
であるとする.すると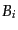 が任意に与えられたとき,
が任意に与えられたとき,
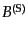 は方程式
は方程式
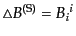 の解として求まり,その解を用いて
の解として求まり,その解を用いて
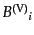 は
は
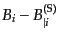 で与えられるので,この分解
は一意的である.同様に、テンソル量
で与えられるので,この分解
は一意的である.同様に、テンソル量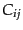 は
は
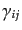 に比例する部
分、スカラーの共変微分として得られる部分、ベクトルの共変微分として得ら
れる部分に分けて、
に比例する部
分、スカラーの共変微分として得られる部分、ベクトルの共変微分として得ら
れる部分に分けて、
![$\displaystyle C_{ij} = \gamma_{ij} D + {C^{\rm (S)}}_{\vert ij} + \frac12 \left[ {C^{\rm (V)}}_{i\vert j} + {C^{\rm (V)}}_{j\vert i}\right] + {C^{\rm (T)}}_{ij}$](img3044.png) |
(J.3.49) |
と分解する。ここで、ベクトル型成分からはスカラーが,テンソル型成分から
はスカラーとベクトルが作れないものにする.その条件は
| |
|
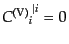 |
(J.3.50) |
| |
|
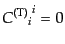 |
(J.3.51) |
| |
|
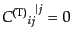 |
(J.3.52) |
である.この分解が一意的であることを見るため,非摂動時空の3次元曲率テ
ンソルの形(2.2.16)と,式(B.2.69)のように与えられる3次
元空間における共変微分の交換関係を繰り返し使えば,上の条件を満たすとき
| |
|
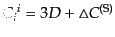 |
(J.3.53) |
| |
|
![$\displaystyle {C_{ij}}^{\vert j}
= D_{\vert i}
+ \left[(\triangle + 2K) C^{\rm (S)})\right]_{\vert i}
+ \frac12 \triangle C^{\rm (V)}_i
+ K C^{\rm (V)}_i$](img3049.png) |
(J.3.54) |
| |
|
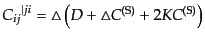 |
(J.3.55) |
となる.すると,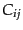 が与えられているとき,連立微分方程式
(10.3.49), (10.3.53)-(10.3.55)を満たす
が与えられているとき,連立微分方程式
(10.3.49), (10.3.53)-(10.3.55)を満たす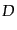 ,
,
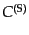 ,
,
 ,
,
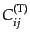 は一意的に定まること
になる.11成分ある自由度のうち、5 つの拘束条件を課して、対称行列
は一意的に定まること
になる.11成分ある自由度のうち、5 つの拘束条件を課して、対称行列
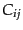 に6つある自由度が固定されることになっている.
に6つある自由度が固定されることになっている.
さて、ここで、ゲージ変換(10.3.44)-(10.3.46)は線形な関係で
表されているので両辺をテンソル型に分解できる。時間移動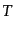 はスカラー型
である。空間移動も分解して、
はスカラー型
である。空間移動も分解して、
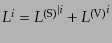 とする。これにより、摂動の成分の変換はスカラー、ベクトル、テン
ソルの各型で独立となる。具体的にはスカラー型について、
とする。これにより、摂動の成分の変換はスカラー、ベクトル、テン
ソルの各型で独立となる。具体的にはスカラー型について、
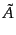 |
 |
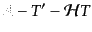 |
(J.3.56) |
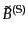 |
 |
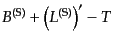 |
(J.3.57) |
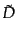 |
 |
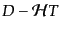 |
(J.3.58) |
 |
 |
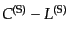 |
(J.3.59) |
ベクトル型について
| |
|
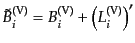 |
(J.3.60) |
| |
|
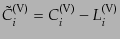 |
(J.3.61) |
また、テンソル型について
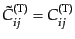 |
(J.3.62) |
となる。





次へ: ゲージ不変量によるアインシュタイン方程式
上へ: 相対論的摂動論
前へ: 計量およびアインシュタインテンソルの摂動
目次
索引
All rights reserved © T.Matsubara 2004-2010
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11
![]() を
考える。ここで
を
考える。ここで![]() は計量の摂動と同じオーダーの微小量とする。この
とき計量の変換は
は計量の摂動と同じオーダーの微小量とする。この
とき計量の変換は
![]() やテンソル量である
やテンソル量である![]() は、こ
のまま扱うよりも、スカラー型、ベクトル型、テンソル型に分解すると扱いや
すくなる.まず、ベクトル量である
は、こ
のまま扱うよりも、スカラー型、ベクトル型、テンソル型に分解すると扱いや
すくなる.まず、ベクトル量である![]() はあるスカラー場
はあるスカラー場
![]() から
生成できる成分とその他の成分に分解して、
から
生成できる成分とその他の成分に分解して、
![]() はスカラー型
である。空間移動も分解して、
はスカラー型
である。空間移動も分解して、
![]() とする。これにより、摂動の成分の変換はスカラー、ベクトル、テン
ソルの各型で独立となる。具体的にはスカラー型について、
とする。これにより、摂動の成分の変換はスカラー、ベクトル、テン
ソルの各型で独立となる。具体的にはスカラー型について、
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11