




次へ: ゲージ変換とスカラー・ベクトル・テンソル分解
上へ: 相対論的摂動論
前へ: ゲージの問題
目次
索引
背景時空はロバートソン・ウォーカー計量(2.1.8)で表される。以降、
時間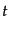 のかわりに、
のかわりに、
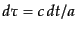 で定義されるコンフォーマル時間
で定義されるコンフォーマル時間
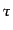 を使うと便利であり、背景時空の計量は
を使うと便利であり、背景時空の計量は
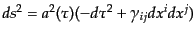 |
(J.2.1) |
となる。ここで、
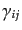 は一様等方な3次元計量で、球座標表示では
は一様等方な3次元計量で、球座標表示では
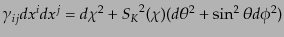 |
(J.2.2) |
である。実際の宇宙の計量
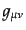 を、次のように非摂動成分
を、次のように非摂動成分
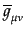 と、摂動成分
と、摂動成分
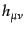 に分解する:
に分解する:
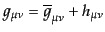 |
(J.2.3) |
時間成分はこの章では以後コンフォーマル時間を用いる(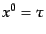 )。非摂動
成分
)。非摂動
成分
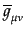 はロバートソン・ウォーカー計量(10.2.1)で表
される。非摂動成分を固定して、上の計量の形をアインシュタイン方程式へ入
れて解けば、摂動宇宙の進化が決められることになる。だが、全く一般の場合
の解を求めることは、アインシュタイン方程式の一般解を求める問題と同等で
あり、現実的には不可能である。そこで我々は何らかの有効な近似の下にこれ
を解くことになる。
はロバートソン・ウォーカー計量(10.2.1)で表
される。非摂動成分を固定して、上の計量の形をアインシュタイン方程式へ入
れて解けば、摂動宇宙の進化が決められることになる。だが、全く一般の場合
の解を求めることは、アインシュタイン方程式の一般解を求める問題と同等で
あり、現実的には不可能である。そこで我々は何らかの有効な近似の下にこれ
を解くことになる。
現実的には、我々の宇宙は平均的には極端な時空計量のゆらぎはない。ブラッ
クホールのまわりのようにごく限られた領域でのみ計量のゆらぎが大きくなっ
ているが、それ以外の場所では摂動部分
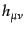 は小さくなっている。そ
こで、計量の摂動について2次以上の項を無視しても宇宙の大局的な非一様性
を近似的に表すことに問題はないと考えられる。そこで、これ以後摂動の1次
までの近似の下に方程式を解くことにする。
は小さくなっている。そ
こで、計量の摂動について2次以上の項を無視しても宇宙の大局的な非一様性
を近似的に表すことに問題はないと考えられる。そこで、これ以後摂動の1次
までの近似の下に方程式を解くことにする。
ここで、計量の摂動成分を
と定義される変数で書き直しておくと便利である。ここで、添字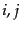 は非摂
動空間の添字と考え、一様等方な空間計量
は非摂
動空間の添字と考え、一様等方な空間計量
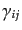 で上げ下げするもの
とする。摂動宇宙の計量は
で上げ下げするもの
とする。摂動宇宙の計量は
![$\displaystyle ds^2 = a^2(\tau) \left[ - (1 + 2A) d\tau^2 - 2 B_i d\tau dx^i + \left(\gamma_{ij} + 2C_{ij}\right) dx^i dx^j \right]$](img2965.png) |
(J.2.7) |
となる。全計量の成分、およびその逆行列の成分は
| |
|
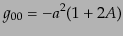 |
(J.2.8) |
| |
|
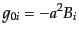 |
(J.2.9) |
| |
|
 |
(J.2.10) |
| |
|
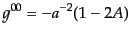 |
(J.2.11) |
| |
|
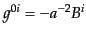 |
(J.2.12) |
| |
|
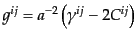 |
(J.2.13) |
となる。したがって、クリストッフェル記号(B.2.44)は
| |
|
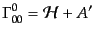 |
(J.2.14) |
| |
|
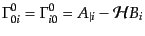 |
(J.2.15) |
| |
|
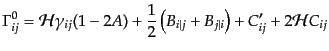 |
(J.2.16) |
| |
|
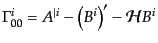 |
(J.2.17) |
| |
|
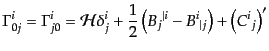 |
(J.2.18) |
| |
|
 |
(J.2.19) |
と計算される。ここで,ダッシュはコンフォーマル時間についての微分を表し,
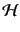 は次式で与えられる.
は次式で与えられる.
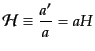 |
(J.2.20) |
ここで,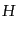 は時間依存するハッブルパラメータである.また,
は時間依存するハッブルパラメータである.また,
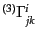 は3次元空間計量
は3次元空間計量
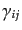 についての3次元ク
リストッフェル記号
についての3次元ク
リストッフェル記号
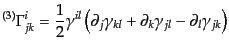 |
(J.2.21) |
である。また、''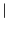 ''は同じ計量
''は同じ計量
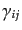 に関する3次元共変微分
に関する3次元共変微分
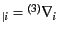 を表す。曲率テンソルをこれらのクリストッフェ
ル記号から式(B.2.62)の定義により求める。対称性(B.2.63) お
よび(B.2.64)から明らかでない成分は
を表す。曲率テンソルをこれらのクリストッフェ
ル記号から式(B.2.62)の定義により求める。対称性(B.2.63) お
よび(B.2.64)から明らかでない成分は
| |
|
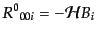 |
(J.2.22) |
| |
|
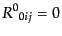 |
(J.2.23) |
| |
|
![$\displaystyle {R^0}_{i0j} =
\left[
{\cal H}' (1 - 2A) - {\cal H}A'
\right] ...
...a_{ij}
- A_{\vert ij}
+ \left(B_{(i\vert j)}\right)' + {\cal H}B_{(i\vert j)}$](img2986.png) |
|
| |
|
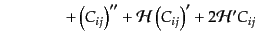 |
(J.2.24) |
| |
|
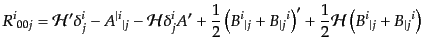 |
|
| |
|
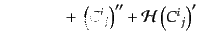 |
(J.2.25) |
| |
|
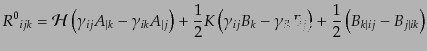 |
|
| |
|
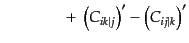 |
(J.2.26) |
| |
|
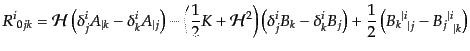 |
|
| |
|
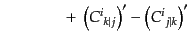 |
(J.2.27) |
| |
|
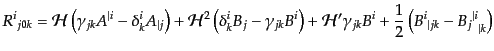 |
|
| |
|
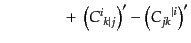 |
(J.2.28) |
| |
|
![$\displaystyle {R^i}_{jkl} =
\left[K + {\cal H}^2 (1 - 2A) \right]
\left(\delta^i_k \gamma_{jl} - \delta^i_l \gamma_{jk}\right)$](img2996.png) |
|
| |
|
![$\displaystyle \qquad\qquad
+\; {\cal H}
\left(\delta^i_k B_{(j\vert l)} - \de...
...}\right)
- \gamma_{jk} \left({B^i}_{\vert l} + {B_l}^{\vert i}\right)
\right]$](img2997.png) |
|
| |
|
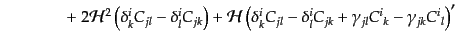 |
|
| |
|
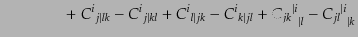 |
(J.2.29) |
となる。これを縮約してリッチテンソルは
| |
|
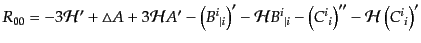 |
(J.2.30) |
| |
|
![$\displaystyle R_{0i} =
2 {\cal H}A_{\vert i}
- \left[
K + {\cal H}' + 2{\cal H}^2
\right] B_i
+ \frac12 \triangle B_i - \frac12 {B^j}_{\vert ji}$](img3001.png) |
|
| |
|
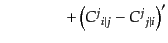 |
(J.2.31) |
| |
|
![$\displaystyle R_{ij} =
\gamma_{ij}
\left\{
2K
+ \left[
{\cal H}'
+ 2 {\cal H}^2
\right] (1 - 2A) - {\cal H}A'
\right\} - A_{\vert ij}$](img3003.png) |
|
| |
|
![$\displaystyle \qquad\qquad
+\; \left[B_{(i\vert j)}\right]' + 2 {\cal H}B_{(i\vert j)}
+ {\cal H}\gamma_{ij} {B^k}_{\vert k}$](img3004.png) |
|
| |
|
![$\displaystyle \qquad\qquad
+\; \left(C_{ij}\right)'' + 2 {\cal H}\left(C_{ij}\...
...} \left( {C^k}_k \right)'
+ 2\left[
2 {\cal H}^2
+ {\cal H}'
\right] C_{ij}$](img3005.png) |
|
| |
|
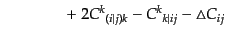 |
(J.2.32) |
となり、さらに添字を上げて、
| |
|
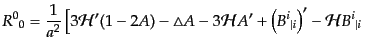 |
|
| |
|
![$\displaystyle \qquad\qquad\qquad
\left.
+ \left({C^i}_i\right)''
+ {\cal H}\left({C^i}_i\right)'
\right]$](img3008.png) |
(J.2.33) |
| |
|
![$\displaystyle {R^0}_i =
- \frac{1}{a^2}
\left[
2 {\cal H}A_{\vert i}
+ K B...
... {B^k}_{\vert ki}
+ \left({C^k}_{i\vert k} - {C^k}_{k\vert i}\right)'
\right]$](img3009.png) |
(J.2.34) |
| |
|
![$\displaystyle {R^i}_0 =
\frac{1}{a^2}
\left\{
2 {\cal H}A^{\vert i}
- \lef...
...ht] B^i
+ \frac12 \triangle B^i - \frac12 {{B^k}_{\vert k}}^{\vert i}
\right.$](img3010.png) |
|
| |
|
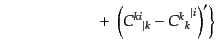 |
(J.2.35) |
| |
|
![$\displaystyle {R^i}_j =
\frac{1}{a^2}
\left\{
\delta^i_j
\left[ 2K + \left(...
...H}^2 \right) (1 - 2A)
- {\cal H}A'
\right] - {A^{\vert i}}_{\vert j}
\right.$](img3012.png) |
|
| |
|
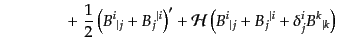 |
|
| |
|
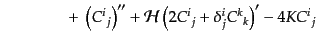 |
|
| |
|
 |
(J.2.36) |
となる。さらに縮約してスカラー曲率は
| |
|
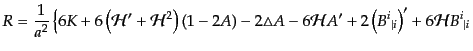 |
|
| |
|
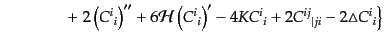 |
(J.2.37) |
となる。こうして、アインシュタインテンソルが次のように求まる。
| |
|
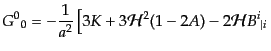 |
|
| |
|
![$\displaystyle \qquad\qquad\qquad
\left.
- 2 {\cal H}\left({C^i}_i\right)'
+ 2K {C^i}_i - {C^{ij}}_{\vert ji} + \triangle {C^i}_i
\right]$](img3019.png) |
(J.2.38) |
| |
|
![$\displaystyle {G^0}_i =
- \frac{1}{a^2}
\left[
2 {\cal H}A_{\vert i}
+ K B...
... {B^k}_{\vert ki}
+ \left({C^k}_{i\vert k} - {C^k}_{k\vert i}\right)'
\right]$](img3020.png) |
(J.2.39) |
| |
|
![$\displaystyle {G^i}_0 =
\frac{1}{a^2}
\left\{
2 {\cal H}A^{\vert i}
- \lef...
...ht] B^i
+ \frac12 \triangle B^i - \frac12 {{B^k}_{\vert k}}^{\vert i}
\right.$](img3021.png) |
|
| |
|
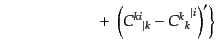 |
(J.2.40) |
| |
|
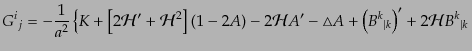 |
|
| |
|
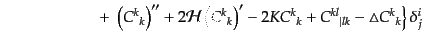 |
|
| |
|
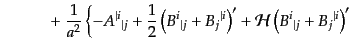 |
|
| |
|
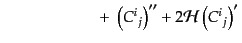 |
|
| |
|
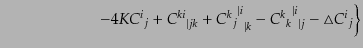 |
(J.2.41) |





次へ: ゲージ変換とスカラー・ベクトル・テンソル分解
上へ: 相対論的摂動論
前へ: ゲージの問題
目次
索引
All rights reserved © T.Matsubara 2004-2010
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11
![]() のかわりに、
のかわりに、
![]() で定義されるコンフォーマル時間
で定義されるコンフォーマル時間
![]() を使うと便利であり、背景時空の計量は
を使うと便利であり、背景時空の計量は
![]() は小さくなっている。そ
こで、計量の摂動について2次以上の項を無視しても宇宙の大局的な非一様性
を近似的に表すことに問題はないと考えられる。そこで、これ以後摂動の1次
までの近似の下に方程式を解くことにする。
は小さくなっている。そ
こで、計量の摂動について2次以上の項を無視しても宇宙の大局的な非一様性
を近似的に表すことに問題はないと考えられる。そこで、これ以後摂動の1次
までの近似の下に方程式を解くことにする。
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11