




次へ: 特殊関数
上へ: 相対性理論の基礎事項
前へ: 特殊相対性理論
目次
索引
Subsections
時空間に曲率がある場合,慣性系を時空間全体に渡って定義することができな
い.この場合,空間全体にわたってデカルト座標を張ることはできないので,
座標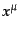 はもっと一般的なものとなる.一般的な座標における微小時空間
隔を
はもっと一般的なものとなる.一般的な座標における微小時空間
隔を
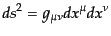 |
(B.2.33) |
で表す.計量テンソル
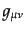 は一般に対称行列を成分にもち,場所の関
数となる.時空がなめらかであれば局所的には慣性系を張ることは可能である.
は一般に対称行列を成分にもち,場所の関
数となる.時空がなめらかであれば局所的には慣性系を張ることは可能である.
座標変換
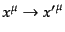 を行うとき,局所的な座標成分の変換
係数を
を行うとき,局所的な座標成分の変換
係数を
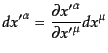 |
(B.2.34) |
のように書く.すると,時空間隔(B.2.33)の局所的ローレンツ不変性に
より,計量テンソルは局所的に
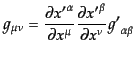 |
(B.2.35) |
のように変換する.
ベクトルは時空上の場所ごとに定義され,座標変換に対して,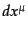 のよう
に変換されるものである:
のよう
に変換されるものである:
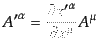 |
(B.2.36) |
添字を下げるには計量テンソルを用いて,
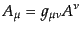 |
(B.2.37) |
とする.逆に添字を上げるには計量テンソル
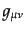 を成分とする行列の
逆行列
を成分とする行列の
逆行列
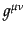 :
:
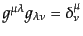 |
(B.2.38) |
を用いて,
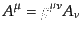 |
(B.2.39) |
となる.共変ベクトルの変換は
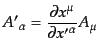 |
(B.2.40) |
となる.高階のテンソルの変換則も明らかであろう.
ある時空上の点に局所慣性系
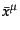 を張ったとき,時空体積素片は
を張ったとき,時空体積素片は
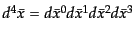 で定義される.
これを一般座標で表せば,計量の変換
で定義される.
これを一般座標で表せば,計量の変換
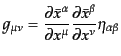 |
(B.2.41) |
から,ヤコビアンは
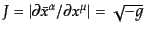 となる.ここで
となる.ここで
 は計量の行列式である.
したがって,一般座標での時空体積素片は
は計量の行列式である.
したがって,一般座標での時空体積素片は
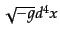 である.
よく使われる関係として,行列式の微分は
である.
よく使われる関係として,行列式の微分は
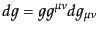 |
(B.2.42) |
である.
一般座標において,スカラーの微分
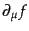 はベクトルとなるが,
ベクトルの微分
はベクトルとなるが,
ベクトルの微分
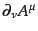 はテンソルとはならない.そこで,微分
の線形性を保ちつつ,ベクトルに作用して2階テンソルを与えるような演算子
を
はテンソルとはならない.そこで,微分
の線形性を保ちつつ,ベクトルに作用して2階テンソルを与えるような演算子
を
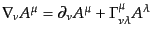 |
(B.2.43) |
により導入し,これを共変微分という.ここで,
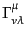 は接続あるいはクリストッフェル記号
と呼ぶ.これは,式(B.2.43)のがテンソルであるという要求により,
は接続あるいはクリストッフェル記号
と呼ぶ.これは,式(B.2.43)のがテンソルであるという要求により,
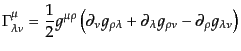 |
(B.2.44) |
で与えられる.局所慣性系のデカルト座標においては計量の一階微分が消える
ため,接続はゼロとなり共変微分は通常の微分に帰着する.その意味で,共変
微分はデカルト座標における微分の,一般座標におけるものへの一般化になって
いる.クリストッフェル記号自身はテンソルではない.
下つき添字のベクトルの共変微分は同じクリストッフェル記号により,
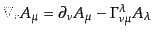 |
(B.2.45) |
である.高階テンソルについては,例えば
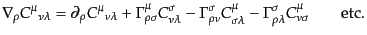 |
(B.2.46) |
などのようになる.一般に共変微分は通常の微分と異なり,可換ではない.共
変微分はセミコロンで表して,例えば式(B.2.46) は
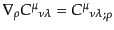 などのように書
かれることもある.これに対して単なる微分はカンマで表し,
などのように書
かれることもある.これに対して単なる微分はカンマで表し,
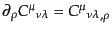 のように書かれ
る.
のように書かれ
る.
スカラー場の微分はそのままでテンソルとなるので,共変微分は通常の微分に
等しい.また,計量テンソルの共変微分は一般的にゼロである:
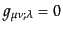 |
(B.2.47) |
また,ベクトルの一般化された発散は
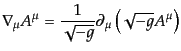 |
(B.2.48) |
という全微分形で与えられる.従って、スカラー場に対する一般化されたダラ
ンベルシアンは
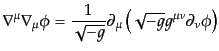 |
(B.2.49) |
となる.
高階テンソルの発散については、それが反対称テンソルであるときのみ
全微分形となる。例えば、
![$\displaystyle \nabla_\nu A^{[\mu\nu]} = \frac{1}{\sqrt{-g}} \partial_\nu \left(\sqrt{-g} A^{[\mu\nu]}\right)$](img4969.png) |
(B.2.50) |
などとなる。
曲がった空間におけるベクトルの平行移動 (parallel transport) の自然な拡
張は局所ローレンツ系での無限小平行移動を考えることによってなされる.そ
の結果,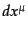 だけ離れた二点間のベクトル
だけ離れた二点間のベクトル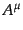 の平行移動による成分
の変化は,
の平行移動による成分
の変化は,
で与えられる.
質点の世界線の軌道は,あるパラメータ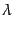 によって
によって
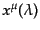 と表すことができる.物質の世界線は,パラメータを適当に取ったときに軌道
の接ベクトル (tangent vector)
と表すことができる.物質の世界線は,パラメータを適当に取ったときに軌道
の接ベクトル (tangent vector)
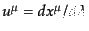 が平行移動をす
る線に沿ったものとなる.この線を測地線 (geodesic)といい,
このときのパラメータをアフィンパラメータという.アフィンパラメー
タでパラメトライズされる測地線を決める方程式は次の測地線方程式
(geodesic equation)である:
が平行移動をす
る線に沿ったものとなる.この線を測地線 (geodesic)といい,
このときのパラメータをアフィンパラメータという.アフィンパラメー
タでパラメトライズされる測地線を決める方程式は次の測地線方程式
(geodesic equation)である:
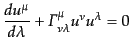 |
(B.2.53) |
あるいは,
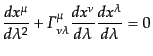 |
(B.2.54) |
アフィンパラメータに一次変換
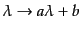 を施し
ても,依然これはアフィンパラメータのままである.平行移動はノルムを変化
させないので,接ベクトル
を施し
ても,依然これはアフィンパラメータのままである.平行移動はノルムを変化
させないので,接ベクトル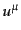 が最初にヌルベクトル (null vector)
が最初にヌルベクトル (null vector)
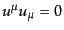 であれば,以後もずっとヌルベクトルであり続ける.これ
をヌル測地線 (null geodesic)という.最初に時間的
(timelike)
であれば,以後もずっとヌルベクトルであり続ける.これ
をヌル測地線 (null geodesic)という.最初に時間的
(timelike)
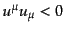 であれば,以後もずっと時間的であり続ける.
これを時間的測地線 (timelike geodesic)という.逆に,最初に
空間的 (spacelike)
であれば,以後もずっと時間的であり続ける.
これを時間的測地線 (timelike geodesic)という.逆に,最初に
空間的 (spacelike)
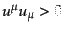 であれば,以後もずっと空間的であり
続ける.これは空間的測地線 (timelike geodesic)となる.
であれば,以後もずっと空間的であり
続ける.これは空間的測地線 (timelike geodesic)となる.
通常の質量をもつ粒子は時間的測地線に従うので,アフィンパラメータの尺度
を適当に選べば,常に
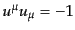 とすることができる.これは,粒
子の4元速度
とすることができる.これは,粒
子の4元速度
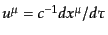 であり,アフィンパラメータ
であり,アフィンパラメータ
 を粒子の固有時
を粒子の固有時 の
の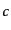 倍に一致させたことになる.この場合
の測地線方程式は
倍に一致させたことになる.この場合
の測地線方程式は
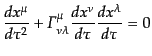 |
(B.2.55) |
である.
光など,質量のない粒子はヌル測地線にしたがう.この場合には
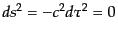 ,つまり固有時はまったく進まないのでこれをアフィンパラ
メータに取ることができない.その代わりに経路に沿って変化する別のアフィ
ンパラメータを用いることになる.このとき,粒子の4元運動量が
,つまり固有時はまったく進まないのでこれをアフィンパラ
メータに取ることができない.その代わりに経路に沿って変化する別のアフィ
ンパラメータを用いることになる.このとき,粒子の4元運動量が
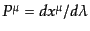 となるようなアフィンパラメータを使えば,測地線方程式
は
となるようなアフィンパラメータを使えば,測地線方程式
は
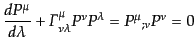 |
(B.2.56) |
となる.この式は粒子に質量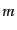 がある場合にも,アフィンパラメータ
を
がある場合にも,アフィンパラメータ
を
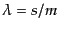 と選べば,測地線方程式(B.2.55)を4元運動量
と選べば,測地線方程式(B.2.55)を4元運動量
 を用いて表したものとなる.
を用いて表したものとなる.
重力以外の通常の物理法則は慣性系において局所的に記述されている.曲がっ
た時空上では常に局所慣性系をとれるので,通常の物理法則をこの局所慣性系
で表して,それを一般座標系で書きなおせば,一般の場合へ拡張したことにな
る.これは,デカルト座標で記述した方程式において,次のような置き換えを
することで簡単に実行できるのである:
| |
|
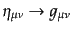 |
(B.2.57) |
| |
|
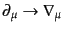 |
(B.2.58) |
ただし,共変微分は非可換演算子なので,この置き換えはベクトルやテンソル
の微分を2回以上含む場合などには不定性が残る.そのような場合には単なる
上の置き換えによる拡張はうまく行かないので他の考察も必要になるが,通常
の問題に対してそのようなことはない.
この手続きによれば,特殊相対論におけるエネルギー・運動量テンソルの表式
(B.1.28)は
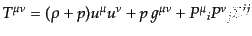 |
(B.2.59) |
となる.また,エネルギー・運動量保存則は
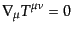 |
(B.2.60) |
で表されることがわかる.
接続は時空の曲がりを記述するが,接続がゼロでなくても必ずしも時空が曲がっ
ているとは限らない.これは,一般座標を考えているので,採用する座標のと
り方によっては時空が平坦であっても接続が存在することがあるからである.
時空の真の曲がりは共変微分の非可換性により特徴づけることができる.すな
わち,任意のベクトル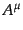 に対して
に対して
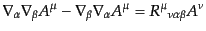 |
(B.2.61) |
で曲率テンソル
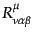 が
が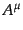 にかかわらずに定義でき,
これが時空の曲がりを表す.平坦な空間においては任意の慣性系でデカルト座
標をとることにより曲率テンソルの全ての成分がゼロになる.一般に全ての成
分がゼロであるテンソルは,どのように座標変換をしても常に全成分はゼロで
ある.したがってこの場合,曲率テンソルは平坦な空間でどう座標を張ろうが
全成分が消えてしまう.これを逆にいえば,曲率テンソルがゼロでない成分を
持つことは,時空が平坦でないことを意味する.式(B.2.61)を共変微分
の定義にもどって書き直すことにより,曲率テンソルは接続で書き表され,
にかかわらずに定義でき,
これが時空の曲がりを表す.平坦な空間においては任意の慣性系でデカルト座
標をとることにより曲率テンソルの全ての成分がゼロになる.一般に全ての成
分がゼロであるテンソルは,どのように座標変換をしても常に全成分はゼロで
ある.したがってこの場合,曲率テンソルは平坦な空間でどう座標を張ろうが
全成分が消えてしまう.これを逆にいえば,曲率テンソルがゼロでない成分を
持つことは,時空が平坦でないことを意味する.式(B.2.61)を共変微分
の定義にもどって書き直すことにより,曲率テンソルは接続で書き表され,
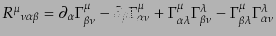 |
(B.2.62) |
となる.曲率テンソルには,その添字に対して,次のような対称性がある:
| |
|
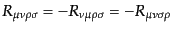 |
(B.2.63) |
| |
|
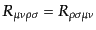 |
(B.2.64) |
| |
|
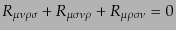 |
(B.2.65) |
| |
|
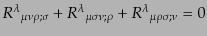 |
(B.2.66) |
最後の式はビアンキ恒等式と呼ばれる.曲率テンソルを一回縮約し
たものをリッチテンソルと言う:
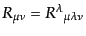 |
(B.2.67) |
さらにもう一度縮約したものはスカラー曲率と言う:
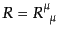 |
(B.2.68) |
曲率テンソルは長さの逆2乗の次元を持つ.従って,長さ
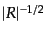 を越え
たスケールでは曲率の効果が顕著となってくる.逆にそれ以下のスケールでは
平坦な空間に近付いていく.
を越え
たスケールでは曲率の効果が顕著となってくる.逆にそれ以下のスケールでは
平坦な空間に近付いていく.
共変微分はスカラーに作用する場合以外一般に非可換で,その交換関係はベク
トルの場合,式(B.2.61)で与えられるが,高階のテンソルについては例
えば,
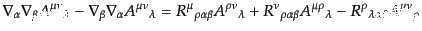 |
(B.2.69) |
などのようになる.
リッチテンソルに含まれる情報はリーマンテンソルに含まれる情報よりも少な
い。リーマンテンソルのうち、リッチテンソルに含まれている情報を除いた成
分をワイルテンソルと呼び、次式で定義される:
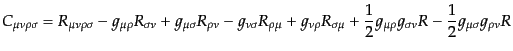 |
(B.2.70) |
ワイルテンソルは添字の入れ換えについてリーマンテンソルの満たす
(B.2.66)と同じ対称性を持ち、さらにリーマンテンソルからリッチテ
ンソルを導くような縮約は消える:
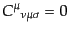 |
(B.2.71) |
重力を支配する方程式は次のアインシュタイン方程式で表される.
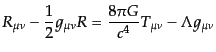 |
(B.2.72) |
ここで,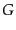 はニュートンの重力定数であり,
はニュートンの重力定数であり,
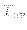 はエネルギー・運
動量テンソルである.また,
はエネルギー・運
動量テンソルである.また,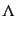 は宇宙定数である.左辺は時空の幾何
学的な量であり,計量テンソルのみで書けている.一方右辺は時空上にふくま
れる物質などのエネルギーで決まる量である.つまり,アインシュタイン方程
式は時空とエネルギー状態の関係を与える法則を表している.左辺はアインシュ
タインテンソルと呼ばれる:
は宇宙定数である.左辺は時空の幾何
学的な量であり,計量テンソルのみで書けている.一方右辺は時空上にふくま
れる物質などのエネルギーで決まる量である.つまり,アインシュタイン方程
式は時空とエネルギー状態の関係を与える法則を表している.左辺はアインシュ
タインテンソルと呼ばれる:
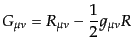 |
(B.2.73) |
ビアンキ恒等式によれば,アインシュタインテンソルは次の恒等式
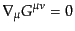 |
(B.2.74) |
を満たすことが分かる.したがって,アインシュタイン方程式は自動的にエネ
ルギー・運動量保存則
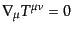 を含んでいることになる.
物質の運動はこの保存則からきまるが,重力場を決める情報はアインシュタイ
ン方程式の中に別に含まれている.
を含んでいることになる.
物質の運動はこの保存則からきまるが,重力場を決める情報はアインシュタイ
ン方程式の中に別に含まれている.
ニュートンの重力理論では重力ポテンシャル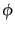 により重力が記述される.
一般相対論を次の条件の下に近似することにより,ニュートン理論が導かれる.
により重力が記述される.
一般相対論を次の条件の下に近似することにより,ニュートン理論が導かれる.
- 考えている系の座標系では,時空は平坦に近く,
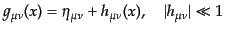 |
(B.2.75) |
が成り立つ.
-
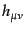 は準静的である.すなわち,考えている系の長さのサイズ
を
は準静的である.すなわち,考えている系の長さのサイズ
を とするとき,
とするとき,
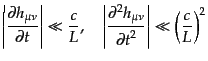 |
(B.2.76) |
が成り立ち,かつ,
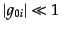 である.
である.
- 物質の運動は非相対論的である.すなわち,物質の速度
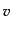 は
は
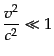 |
(B.2.77) |
をみたす.さらに,
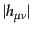 と
と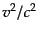 は同じオーダーであるとする.
は同じオーダーであるとする.
アインシュタイン方程式を導く作用は次のアインシュタイン・ヒルベルト作用
である.
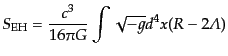 |
(B.2.78) |
また,物質を表す場のラグランジアン密度を
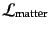 とすれ
ば,全体の作用は
とすれ
ば,全体の作用は
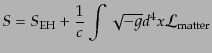 |
(B.2.79) |
となる.この式の変分
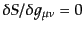 によって運動方程式
をもとめると,アインシュタイン方程式が導かれる.このとき,物質のエネル
ギー運動量テンソル
によって運動方程式
をもとめると,アインシュタイン方程式が導かれる.このとき,物質のエネル
ギー運動量テンソル
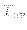 とラグランジアン密度は次のように関係し
ている:
とラグランジアン密度は次のように関係し
ている:
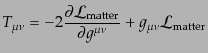 |
(B.2.80) |
例えば、物質場の最も簡単な例として実スカラー場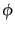 を考えると、そのラ
グランジアン密度は
を考えると、そのラ
グランジアン密度は
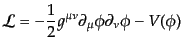 |
(B.2.81) |
で与えられ、その運動方程式
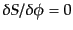 は
は
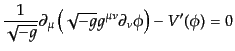 |
(B.2.82) |
あるいは式(B.2.49)のダランベルシアンを使い、
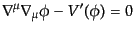 |
(B.2.83) |
となる。また、対称エネルギー運動量テンソル(B.2.80)は、
![$\displaystyle T^{\mu\nu} = \partial^\mu \phi \partial^\nu \phi - g^{\mu\nu} \le...
...ac12 g^{\alpha\beta} \partial_\alpha \phi \partial_\beta \phi + V(\phi) \right]$](img5020.png) |
(B.2.84) |
となる.
なお,式(B.2.78)の作用は時空に境界のない場合のものであり,境界が
存在する場合の作用は以下のようになる:
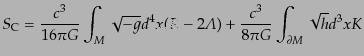 |
(B.2.85) |
ここで, は考えている時空を表す多様体を示し、
は考えている時空を表す多様体を示し、
 はその多様
体の境界を表す。また,
はその多様
体の境界を表す。また,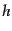 はその境界上での3次元計量
はその境界上での3次元計量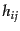 の行列式
の行列式
 である.さらに,
である.さらに,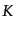 は
は
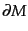 の外曲率
の外曲率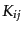 のト
レース
のト
レース
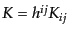 である.外曲率は3次元境界が4次元時空中でど
のように埋め込まれているのかを表すもので次のように定義される.すなわち,
まず境界の3次元面に直交する垂直ベクトル
である.外曲率は3次元境界が4次元時空中でど
のように埋め込まれているのかを表すもので次のように定義される.すなわち,
まず境界の3次元面に直交する垂直ベクトル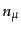 を考える.境界上の3次
元座標を
を考える.境界上の3次
元座標を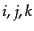 などとして,このベクトルを境界に沿って
などとして,このベクトルを境界に沿って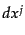 だけ平行移
動したときに,その点でのベクトルのずれを
だけ平行移
動したときに,その点でのベクトルのずれを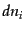 とする.
このとき外曲率は
とする.
このとき外曲率は
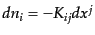 により定義される.このとき,
により定義される.このとき,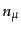 は境界面方向
の成分を持たず,また
は境界面方向
の成分を持たず,また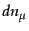 は逆に境界面方向の成分しか持たないから,
は逆に境界面方向の成分しか持たないから,
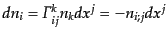 と表される.つまり,
と表される.つまり,
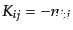 である.
である.
作用から運動方程式を得るときや,摂動を考えるときなど,関数の変分を必要
とする.ここで一般相対論においてよく必要となる幾何学量について,1次変
分の表式をまとめておく.
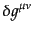 |
 |
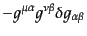 |
(B.2.86) |
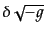 |
 |
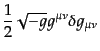 |
(B.2.87) |
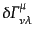 |
 |
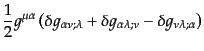 |
(B.2.88) |
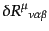 |
 |
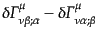 |
|
| |
 |
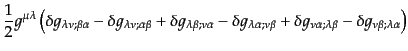 |
(B.2.89) |
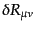 |
 |
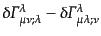 |
|
| |
 |
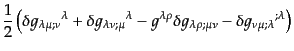 |
(B.2.90) |
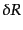 |
 |
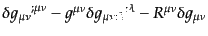 |
(B.2.91) |
重力場の正準形式
ここではADM形式と呼ばれるアインシュタイン重力場の正準形式を導入する.
ここでは特に断らない限り
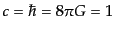 となる自然単位系を用
いる.正準形式には時間変数がなければならない.そこで時空をスライスして,
連続的に時間一定面を定める必要がある.このときの時間変数を
となる自然単位系を用
いる.正準形式には時間変数がなければならない.そこで時空をスライスして,
連続的に時間一定面を定める必要がある.このときの時間変数を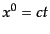 と
し,時刻
と
し,時刻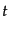 の定める3次元面を
の定める3次元面を
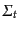 とかく.すると各々の
とかく.すると各々の
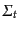 には,4次元計量
には,4次元計量
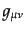 から導かれる計量
から導かれる計量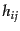 が定義
できる.この計量を持つ
が定義
できる.この計量を持つ
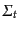 上の3次元座標を
上の3次元座標を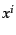 (
(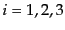 )とす
る.また,計量
)とす
る.また,計量
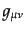 で計った,無限小だけ離れた2つの面
で計った,無限小だけ離れた2つの面
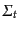 と
と
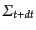 の間の距離を
の間の距離を
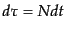 とおく.3次元面
とおく.3次元面
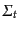 上の点
上の点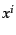 において,この3次元面に垂直なベクトル
において,この3次元面に垂直なベクトル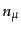 が
3次元面
が
3次元面
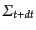 と交わる点は,一般に
と交わる点は,一般に
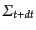 において
において
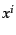 とは異なる座標値を持つ.そこで,前者の交わりの点から面
とは異なる座標値を持つ.そこで,前者の交わりの点から面
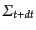 上の座標値
上の座標値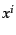 へと向かうベクトルを
へと向かうベクトルを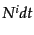 とする.こ
の状況は図B.2 を見れば分かりやすい。
とする.こ
の状況は図B.2 を見れば分かりやすい。
ここで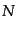 はラプス関数,
はラプス関数,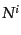 はシフトベクトルと呼ばれる.このような計量
の分解を(3+1)分解という.
はシフトベクトルと呼ばれる.このような計量
の分解を(3+1)分解という.
これらの新変数によれば微小時空間隔は
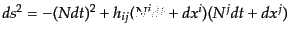 |
(B.2.92) |
と表せるから,もとの4次元時空の計量は
| |
|
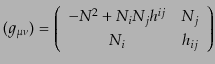 |
(B.2.93) |
| |
|
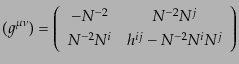 |
(B.2.94) |
という形でなることがわかる.ただし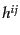 は
は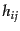 の逆行列,また
の逆行列,また
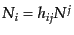 である.このときクラメールの公式により
である.このときクラメールの公式により
 |
(B.2.95) |
が成り立つ.ここで
 ,
,
 である.
である.
さて,外曲率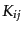 は3次元面
は3次元面
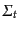 に垂直な単位ベクトル
に垂直な単位ベクトル
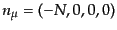 から
から
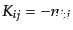 で定義されるから,
で定義されるから,
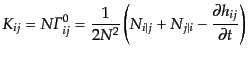 |
(B.2.96) |
と計算される.ただし''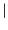 ''は3次元計量
''は3次元計量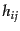 に関する3次元的共変微分
を表す.4次元スカラー曲率
に関する3次元的共変微分
を表す.4次元スカラー曲率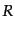 は,多少面倒だが計量(B.2.93),
(B.2.94)から直接計算することにより,次の結果となる:
は,多少面倒だが計量(B.2.93),
(B.2.94)から直接計算することにより,次の結果となる:
![$\displaystyle \sqrt{-g} R = N \sqrt{h} \left({}^{(3)}R - K^2 + K_{ij} K^{ij}\ri...
...ft[ \sqrt{h} \left(KN^i - h^{ij}\frac{\partial N}{\partial x^j} \right) \right]$](img5061.png) |
(B.2.97) |
ここで
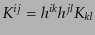 ,
,
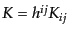 とし,
とし,
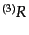 は3次元面
は3次元面
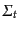 上の3次元スカラー曲率である.
上の3次元スカラー曲率である.
これで時間変数が分離した形で時空が表されたので,次にアインシュタインヒ
ルベルト作用を考える.一般に境界項を含む場合の作用は式(B.2.85):
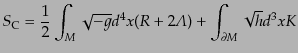 |
(B.2.98) |
で与えられる.これに式(B.2.97)を代入して,さらに空間部分の表面項
は考えないことにして落とせば,
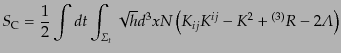 |
(B.2.99) |
となる.この形からただちにラグランジアンが
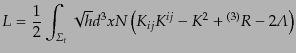 |
(B.2.100) |
であることがわかる.すなわち,重力場に対するラグランジアン形式が(3+1)
分解の形で得られたことになる.
さらに,正準形式へと移行する.力学変数は計量を表す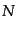 ,
, 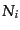 ,
, 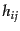 であるから,これらの正準共役変数
であるから,これらの正準共役変数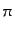 ,
, 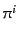 ,
, 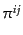 を求めると,
を求めると,
| |
|
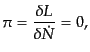 |
(B.2.101) |
| |
|
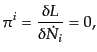 |
(B.2.102) |
| |
|
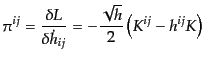 |
(B.2.103) |
となる.ここでドットは時間微分を表し,また変数は空間座標に関して連続変
数であるから汎関数微分が用いられている.ここで式(B.2.101),
(B.2.102)は1次拘束条件を与える.この拘束条件が発生する理由はラ
プス関数やシフトベクトルが力学的な変数ではなく,時間一定面のスライスの
方法,またその中での空間座標の変化,という本来の時空とは関係のない人工
的な操作から得られたものだからである.ともかく,これらの正準共役変数に
よりハミルトニアンを構成すると,
となる.ここで
を定義した.1次拘束条件が時間的に常に成り立つことにより,2次拘束条件
が導かれる.ポアソン括弧
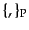 により,いまの場合,
により,いまの場合,
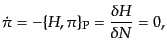 |
|
|
(B.2.107) |
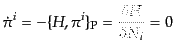 |
|
|
(B.2.108) |
となるから,2次拘束条件は
| |
|
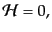 |
(B.2.109) |
| |
|
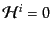 |
(B.2.110) |
である.計算はたいへん面倒だが,これら都合8つの拘束条件
(B.2.101), (B.2.102), (B.2.109), (B.2.110)の他
には拘束条件は発生せず,さらにすべて第1類の拘束であることを確かめるこ
とができる.その結果は
| |
|
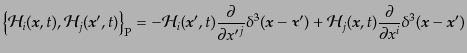 |
(B.2.111) |
| |
|
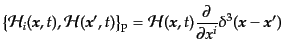 |
(B.2.112) |
| |
|
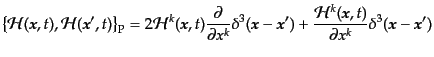 |
(B.2.113) |
である.ここで,ハミルトニアン(B.2.104)は拘束条件とそのラグランジュ
未定定数のみで書けてしまっていることに注意しよう.この事実は重力場が力
学系として特異なものであることを物語っている.すなわち,ハミルトニアン
には運動エネルギーに対応する項がなく,系の時間変化を記述するような力学
的な内容は何も含まれていないのである.系の力学的な内容は拘束条件の中に
含まれているのである.重力場の正準形式がこのような特異なものになる本質
的な理由はもともと系が一般座標変換に対して不変であることにある.通常の
力学系では系の時間発展を解くことによって運動が得られるが,一般相対論に
おいては時間の経過そのものが力学変数によって決まるという他の力学系では
考えられない性質を持っている.





次へ: 特殊関数
上へ: 相対性理論の基礎事項
前へ: 特殊相対性理論
目次
索引
All rights reserved © T.Matsubara 2004-2010
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11
![]() はもっと一般的なものとなる.一般的な座標における微小時空間
隔を
はもっと一般的なものとなる.一般的な座標における微小時空間
隔を
![]() を行うとき,局所的な座標成分の変換
係数を
を行うとき,局所的な座標成分の変換
係数を
![]() のよう
に変換されるものである:
のよう
に変換されるものである:
![]() を張ったとき,時空体積素片は
を張ったとき,時空体積素片は
![]() で定義される.
これを一般座標で表せば,計量の変換
で定義される.
これを一般座標で表せば,計量の変換
![]() はベクトルとなるが,
ベクトルの微分
はベクトルとなるが,
ベクトルの微分
![]() はテンソルとはならない.そこで,微分
の線形性を保ちつつ,ベクトルに作用して2階テンソルを与えるような演算子
を
はテンソルとはならない.そこで,微分
の線形性を保ちつつ,ベクトルに作用して2階テンソルを与えるような演算子
を
![]() だけ離れた二点間のベクトル
だけ離れた二点間のベクトル![]() の平行移動による成分
の変化は,
の平行移動による成分
の変化は,
![]() によって
によって
![]() と表すことができる.物質の世界線は,パラメータを適当に取ったときに軌道
の接ベクトル (tangent vector)
と表すことができる.物質の世界線は,パラメータを適当に取ったときに軌道
の接ベクトル (tangent vector)
![]() が平行移動をす
る線に沿ったものとなる.この線を測地線 (geodesic)といい,
このときのパラメータをアフィンパラメータという.アフィンパラメー
タでパラメトライズされる測地線を決める方程式は次の測地線方程式
(geodesic equation)である:
が平行移動をす
る線に沿ったものとなる.この線を測地線 (geodesic)といい,
このときのパラメータをアフィンパラメータという.アフィンパラメー
タでパラメトライズされる測地線を決める方程式は次の測地線方程式
(geodesic equation)である:
![]() を施し
ても,依然これはアフィンパラメータのままである.平行移動はノルムを変化
させないので,接ベクトル
を施し
ても,依然これはアフィンパラメータのままである.平行移動はノルムを変化
させないので,接ベクトル![]() が最初にヌルベクトル (null vector)
が最初にヌルベクトル (null vector)
![]() であれば,以後もずっとヌルベクトルであり続ける.これ
をヌル測地線 (null geodesic)という.最初に時間的
(timelike)
であれば,以後もずっとヌルベクトルであり続ける.これ
をヌル測地線 (null geodesic)という.最初に時間的
(timelike)
![]() であれば,以後もずっと時間的であり続ける.
これを時間的測地線 (timelike geodesic)という.逆に,最初に
空間的 (spacelike)
であれば,以後もずっと時間的であり続ける.
これを時間的測地線 (timelike geodesic)という.逆に,最初に
空間的 (spacelike)
![]() であれば,以後もずっと空間的であり
続ける.これは空間的測地線 (timelike geodesic)となる.
であれば,以後もずっと空間的であり
続ける.これは空間的測地線 (timelike geodesic)となる.
![]() とすることができる.これは,粒
子の4元速度
とすることができる.これは,粒
子の4元速度
![]() であり,アフィンパラメータ
であり,アフィンパラメータ
![]() を粒子の固有時
を粒子の固有時![]() の
の![]() 倍に一致させたことになる.この場合
の測地線方程式は
倍に一致させたことになる.この場合
の測地線方程式は
![]() ,つまり固有時はまったく進まないのでこれをアフィンパラ
メータに取ることができない.その代わりに経路に沿って変化する別のアフィ
ンパラメータを用いることになる.このとき,粒子の4元運動量が
,つまり固有時はまったく進まないのでこれをアフィンパラ
メータに取ることができない.その代わりに経路に沿って変化する別のアフィ
ンパラメータを用いることになる.このとき,粒子の4元運動量が
![]() となるようなアフィンパラメータを使えば,測地線方程式
は
となるようなアフィンパラメータを使えば,測地線方程式
は
![]() に対して
に対して
![]() により重力が記述される.
一般相対論を次の条件の下に近似することにより,ニュートン理論が導かれる.
により重力が記述される.
一般相対論を次の条件の下に近似することにより,ニュートン理論が導かれる.
![]() を考えると、そのラ
グランジアン密度は
を考えると、そのラ
グランジアン密度は
![]() となる自然単位系を用
いる.正準形式には時間変数がなければならない.そこで時空をスライスして,
連続的に時間一定面を定める必要がある.このときの時間変数を
となる自然単位系を用
いる.正準形式には時間変数がなければならない.そこで時空をスライスして,
連続的に時間一定面を定める必要がある.このときの時間変数を![]() と
し,時刻
と
し,時刻![]() の定める3次元面を
の定める3次元面を
![]() とかく.すると各々の
とかく.すると各々の
![]() には,4次元計量
には,4次元計量
![]() から導かれる計量
から導かれる計量![]() が定義
できる.この計量を持つ
が定義
できる.この計量を持つ
![]() 上の3次元座標を
上の3次元座標を![]() (
(![]() )とす
る.また,計量
)とす
る.また,計量
![]() で計った,無限小だけ離れた2つの面
で計った,無限小だけ離れた2つの面
![]() と
と
![]() の間の距離を
の間の距離を
![]() とおく.3次元面
とおく.3次元面
![]() 上の点
上の点![]() において,この3次元面に垂直なベクトル
において,この3次元面に垂直なベクトル![]() が
3次元面
が
3次元面
![]() と交わる点は,一般に
と交わる点は,一般に
![]() において
において
![]() とは異なる座標値を持つ.そこで,前者の交わりの点から面
とは異なる座標値を持つ.そこで,前者の交わりの点から面
![]() 上の座標値
上の座標値![]() へと向かうベクトルを
へと向かうベクトルを![]() とする.こ
の状況は図B.2 を見れば分かりやすい。
とする.こ
の状況は図B.2 を見れば分かりやすい。
![]() は3次元面
は3次元面
![]() に垂直な単位ベクトル
に垂直な単位ベクトル
![]() から
から
![]() で定義されるから,
で定義されるから,
![]() ,
, ![]() ,
, ![]() であるから,これらの正準共役変数
であるから,これらの正準共役変数![]() ,
, ![]() ,
, ![]() を求めると,
を求めると,
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11