




次へ: いくつかのゲージ固定との関係
上へ: 相対論的摂動論
前へ: ゲージ変換とスカラー・ベクトル・テンソル分解
目次
索引
Subsections
さて、上のようなテンソルの型による分解を行うと、ゲージ自由度を消し去っ
て、物理的自由度のみを残して摂動の振舞いを調べることが可能になる。アイ
ンシュタイン方程式
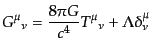 |
(J.4.63) |
を背景時空の方程式
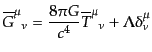 |
(J.4.64) |
とその摂動部分
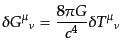 |
(J.4.65) |
に分けて、さらに、摂動部分は上のテンソルの型によって分類する。そしてこ
れをゲージによらない形に書き直したい。これを以下に実行する。
背景時空の方程式は以前求めたフリードマン・ルメートルモデルであるが、こ
れをコンフォーマル時間を使った式に書き直しておこう。まず、上で求めたア
インシュタインテンソル(10.2.38)-(10.2.41)の非摂動部分から
| |
|
![$\displaystyle {{\overline{G}}^0}_0 =
- \frac{3}{a^2} \left[{\cal H}^2 + K\right]$](img3070.png) |
(J.4.66) |
| |
|
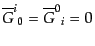 |
(J.4.67) |
| |
|
![$\displaystyle {{\overline{G}}^i}_j =
- \frac{1}{a^2}
\left[
2 {\cal H}'
+ {\cal H}^2 + K
\right] \delta^i_j$](img3072.png) |
(J.4.68) |
である。したがって、アインシュタイン方程式は
| |
|
![$\displaystyle \frac{1}{a^2} \left[{\cal H}^2 + K\right]
= - \frac{8 \pi G}{3c^4} {\overline{T}^0}_0
+ \frac{\Lambda}{3}$](img3073.png) |
(J.4.69) |
| |
|
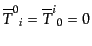 |
(J.4.70) |
| |
|
![$\displaystyle \frac{1}{a^2}
\left[
2 {\cal H}'
+ {\cal H}^2 + K
\right] \delta^i_j
= - \frac{8 \pi G}{c^4} {\overline{T}^i}_j
+ \Lambda \delta^i_j$](img3075.png) |
(J.4.71) |
となる。非摂動エネルギー運動量テンソルは
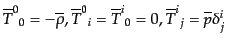 であるから、これらの方程式は次のものに同値である。
であるから、これらの方程式は次のものに同値である。
| |
|
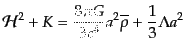 |
(J.4.72) |
| |
|
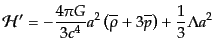 |
(J.4.73) |
さらに、これら2つの式から導かれるエントロピー保存の式は
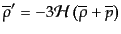 |
(J.4.74) |
である。時間依存する宇宙論パラメータと圧力-密度比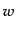 は,
は,
| |
|
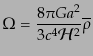 |
(J.4.75) |
| |
|
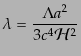 |
(J.4.76) |
| |
|
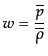 |
(J.4.77) |
で与えられ,上の式をこれらのパラメータにより書き直した式が有用で
ある:
| |
|
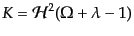 |
(J.4.78) |
| |
|
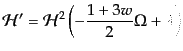 |
(J.4.79) |
| |
|
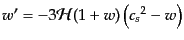 |
(J.4.80) |
ここで、背景時空はエントロピー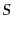 を保存しているので、
を保存しているので、
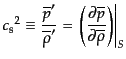 |
(J.4.81) |
は音速に対応する。式(10.4.78), (10.4.79)から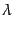 を消去した式
を消去した式
も有用である.摂動項の計算において,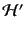 ,
, 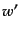 が現れてきたらこれら
の関係式によって消去してよい.
が現れてきたらこれら
の関係式によって消去してよい.
まず、テンソル型摂動計量
 については式(10.3.62)により、
それ自身ゲージ不変である。これはもともと座標変換の自由度であるゲージ変
換にはテンソル型の成分は含まれていないからである。アインシュタインテン
ソルの摂動部分について、テンソル型摂動の寄与を取り出すと次のようになる。
については式(10.3.62)により、
それ自身ゲージ不変である。これはもともと座標変換の自由度であるゲージ変
換にはテンソル型の成分は含まれていないからである。アインシュタインテン
ソルの摂動部分について、テンソル型摂動の寄与を取り出すと次のようになる。
したがって、テンソル型の運動方程式は
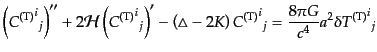 |
(J.4.85) |
となり、これはそのままゲージ不変な方程式である。
次に、ベクトル型摂動計量
 を考える。これら
はゲージに依存するので、ゲージ自由度を含まないような線形な組合せとして
を考える。これら
はゲージに依存するので、ゲージ自由度を含まないような線形な組合せとして
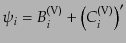 |
(J.4.86) |
を作ることができる。これ以外のゲージ不変な組合せはない。運動方程式であ
るアインシュタイン方程式はもちろんゲージ変換で不変であり、ゲージ自由度
を決める情報は含まれ得ないので、このゲージ不変な変数のみが現れて来るは
ずである。そこでアインシュタインテンソルの摂動部分について、ベクトル型
摂動の寄与を取り出すと次のようになる。
| |
|
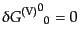 |
(J.4.87) |
| |
|
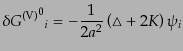 |
(J.4.88) |
| |
|
![$\displaystyle \delta {{G^{\rm (V)}}^i}_0 =
\frac{1}{2a^2}
\left\{
\left( \tr...
...si^i
+ 4 \left[ {\cal H}'
- {\cal H}^2 - K
\right] {B^{\rm (V)}}^i
\right\}$](img3101.png) |
(J.4.89) |
| |
|
![$\displaystyle \delta {{G^{\rm (V)}}^i}_j =
\frac{1}{2a^2}
\left[
\left( {\ps...
...)'
+ 2 {\cal H}\left( {\psi^i}_{\vert j} + {\psi_j}^{\vert i} \right)
\right]$](img3102.png) |
(J.4.90) |
この式の導出には、3次元空間における共変微分の交換関係を繰り返し使った.
また,ゲージ不変量(10.4.65)を用いて
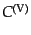 を消去した.アイ
ンシュタイン方程式において、
を消去した.アイ
ンシュタイン方程式において、
 成分と
成分と
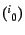 成分は同値
な方程式を与えるので、結局ベクトル型の運動方程式は
成分は同値
な方程式を与えるので、結局ベクトル型の運動方程式は
| |
|
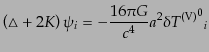 |
(J.4.91) |
| |
|
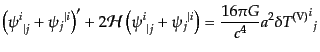 |
(J.4.92) |
となる。
ここで、左辺はゲージ不変量だけで書けているので、どのような運動量エネル
ギーテンソルであろうとも、右辺の
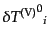 および
および
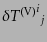 はゲージ不変となるはずである。一方、
はゲージ不変となるはずである。一方、
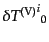 は一般にはゲージ不変ではない。
は一般にはゲージ不変ではない。
スカラー型摂動計量のゲージ変換(10.3.56)-(10.3.59) におい
ては、ゲージ自由度が(空間の一点あたり)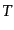 および
および
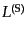 の2つなの
で、4つあるスカラー摂動のうち、物理的自由度は2つである。これは、ゲー
ジ変換を受けないような線形結合を作ることにより取り出すことができる。そ
のような組合せのうち、もっとも簡単なものは次のようなものである。
の2つなの
で、4つあるスカラー摂動のうち、物理的自由度は2つである。これは、ゲー
ジ変換を受けないような線形結合を作ることにより取り出すことができる。そ
のような組合せのうち、もっとも簡単なものは次のようなものである。
| |
|
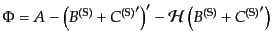 |
(J.4.93) |
| |
|
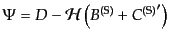 |
(J.4.94) |
もちろん、この2つのどんな線形結合も当然ゲージ不変であるから、この他に
も無限にゲージ不変な組合せを作ることが可能である。ところが、ここに上げ
た組合せは特に簡単であり、以降とても有用である。このようなゲージ不変量
の組合せの自由度は通常のゲージ場の理論においてもよく知られている。電磁
気学において、ゲージ自由度を含まない量として電場と磁場が選べるが、この
2つの線形結合もやはりゲージ自由度を含まない。ところが、電場と磁場は特
別な役割を果たしていることは明らかであろう。ここでもポテンシャル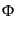 と
と を選ぶことにより、以後の方程式が特に簡単になるのである。
を選ぶことにより、以後の方程式が特に簡単になるのである。
このゲージ不変ポテンシャルを使ってアインシュタインテンソルの摂動部分へ
のスカラー摂動の寄与から変数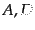 を消去すれば、
を消去すれば、
| |
|
 |
|
| |
|
![$\displaystyle \qquad\qquad\qquad
\left.
+\; 3 {\cal H}
\left[
{\cal H}^2
- {\cal H}' + K
\right] \left( B^{\rm (S)} + {C^{\rm (S)}}' \right)
\right\}$](img3117.png) |
(J.4.95) |
| |
|
![$\displaystyle \delta {{G^{\rm (S)}}^0}_i =
- \frac{2}{a^2}
\left\{
{\cal H}\...
...}' + K
\right] \left( B^{\rm (S)} + {C^{\rm (S)}}' \right)
\right\}_{\vert i}$](img3118.png) |
(J.4.96) |
| |
|
![$\displaystyle \delta {{G^{\rm (S)}}^i}_0 =
\frac{2}{a^2}
\left\{
{\cal H}\Ph...
...\left[
{\cal H}^2
- {\cal H}' + K
\right] {C^{\rm (S)}}'
\right\}^{\vert i}$](img3119.png) |
(J.4.97) |
| |
|
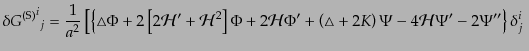 |
|
| |
|
![$\displaystyle \qquad\quad
\left.\left.
- {\left(\Phi + \Psi \right)^{\vert i}...
...ht]
\left( B^{\rm (S)} + {C^{\rm (S)}}' \right) \delta^i_j
\right]\!\!\right]$](img3121.png) |
(J.4.98) |
と計算される。ここでも,3次元空間における共変微分の交換関係を繰り返し
使った.ここで、アインシュタインテンソルのスカラー成分はいずれもゲージ
不変でないことがわかる。そこで、アインシュタインテンソルのゲージ変換を、
式(10.3.42)-(10.3.43)と同様にして求めてみる。背景時空では
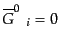 であり、また、
であり、また、
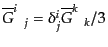 と書けることに注意すれば摂動部のゲー
ジ変換
と書けることに注意すれば摂動部のゲー
ジ変換
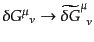 は
は
| |
|
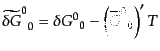 |
(J.4.99) |
| |
|
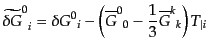 |
(J.4.100) |
| |
|
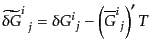 |
(J.4.101) |
となることがわかる。これらのゲージ変換はスカラー型であり、実際、テンソ
ル型やベクトル型ではこれらのアインシュタインテンソルの成分がゲージ不変
になっていることは、上で具体的に見た通りである。スカラー型摂動のゲージ
変換はこの式のように背景時空のアインシュタインテンソルで書き表される。
それに対応して、式(10.4.95), (10.4.96), (10.4.98)の
ゲージ依存項も背景時空のアインシュタインテンソルで表されることは容易に
確かめられる。
そこで、ゲージ不変なアインシュタインテンソルのスカラー摂動
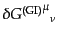 を次のように構成する。
を次のように構成する。
| |
|
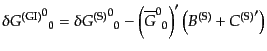 |
(J.4.102) |
| |
|
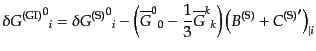 |
(J.4.103) |
| |
|
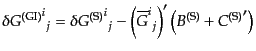 |
(J.4.104) |
すると、実際に式(10.4.95)-(10.4.98)のゲージ依存項は打ち消
しあって、
| |
|
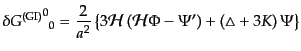 |
(J.4.105) |
| |
|
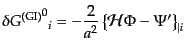 |
(J.4.106) |
| |
|
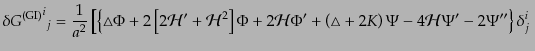 |
|
| |
|
![$\displaystyle \qquad\qquad\qquad
\left.\left.
- {\left(\Phi + \Psi \right)^{\vert i}}_{\vert j}
\right]\!\!\right]$](img3135.png) |
(J.4.107) |
となる。エネルギー運動量テンソルについても次のようにゲージ不変なスカラー
摂動
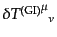 を構成する。
を構成する。
| |
|
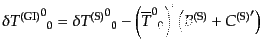 |
(J.4.108) |
| |
|
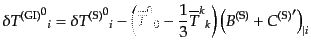 |
(J.4.109) |
| |
|
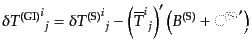 |
(J.4.110) |
そうすれば背景時空の運動方程式(10.4.64)により、結局スカラー摂動
部分の運動方程式はゲージ不変な形
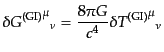 |
(J.4.111) |
となる。ここで、成分
 は成分
は成分
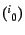 と同値なものなので考
えないことにすれば、左辺は式(10.4.106)-(10.4.108)によりゲー
ジ不変ポテンシャル
と同値なものなので考
えないことにすれば、左辺は式(10.4.106)-(10.4.108)によりゲー
ジ不変ポテンシャル
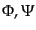 のみで与えられているので、あとは右辺を式
(10.4.109)-(10.4.111)により具体的に構成すれば最終的に運動方
程式が計量の摂動についてゲージ不変な形で与えられることになる。
のみで与えられているので、あとは右辺を式
(10.4.109)-(10.4.111)により具体的に構成すれば最終的に運動方
程式が計量の摂動についてゲージ不変な形で与えられることになる。
エネルギー・運動量テンソルの表式(B.1.28)からその摂動部分を求め
る。まずこの表式に現れてくる4元速度は規格化条件
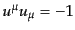 によ
り自由度は3である。この3つの自由度を空間的速度
によ
り自由度は3である。この3つの自由度を空間的速度
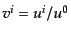 に取る。
非摂動時空では等方
に取る。
非摂動時空では等方
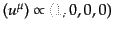 であるから、
であるから、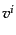 は摂動の
1次の量である。この自由度により、一次までのオーダーで
は摂動の
1次の量である。この自由度により、一次までのオーダーで
| |
|
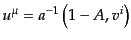 |
(J.4.112) |
| |
|
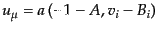 |
(J.4.113) |
という形になる。ここから、射影テンソル
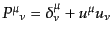 は次のようになる。
は次のようになる。
| |
|
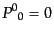 |
(J.4.114) |
| |
|
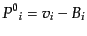 |
(J.4.115) |
| |
|
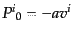 |
(J.4.116) |
| |
|
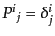 |
(J.4.117) |
これらの表式を、エネルギー・運動量テンソル(B.1.28)の表
式に入れれば一次までのオーダーで、
| |
|
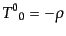 |
(J.4.118) |
| |
|
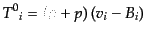 |
(J.4.119) |
| |
|
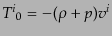 |
(J.4.120) |
| |
|
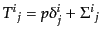 |
(J.4.121) |
を得る。ここで、エネルギー密度を非摂動部と摂動部に分けて、
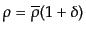 と書く。ここで、
と書く。ここで、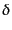 はエネルギー密度ゆらぎ
である。圧力のゆらぎは
はエネルギー密度ゆらぎ
である。圧力のゆらぎは
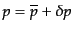 と分ける。非等方ストレス
と分ける。非等方ストレス
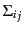 は摂動の一次であるが、これを無次元化した非等方ストレス
は摂動の一次であるが、これを無次元化した非等方ストレス
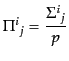 |
(J.4.122) |
で表すのが普通である。これらにより、エネルギー運動量テンソルの摂動部は
次のようになる。
| |
|
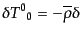 |
(J.4.123) |
| |
|
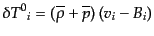 |
(J.4.124) |
| |
|
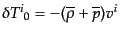 |
(J.4.125) |
| |
|
 |
(J.4.126) |
上に求めたエネルギー運動量テンソルにより、運動方程式をゲージ不変量に対
して求めよう。まず、テンソル型摂動の運動方程式はそのままゲージ不変であ
る。エネルギー運動量テンソルについてはテンソル型摂動は非等方ストレスの
みに含まれていて、
| |
|
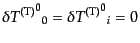 |
(J.4.127) |
| |
|
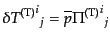 |
(J.4.128) |
となる。非等方ストレスは一次の摂動であるから、(一次近似で)ゲージ不変で
あり、確かに上式はそのままゲージ不変である。したがって、テンソル型摂動
の運動方程式(10.4.85)は
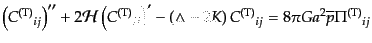 |
(J.4.129) |
となる。ここで、3次元計量
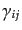 を用いて添字を下げた。テンソル型摂動
はトレースと発散がなく重力波の自由度に対応する。上の式は重力波の膨張宇
宙における波動方程式となっている。
を用いて添字を下げた。テンソル型摂動
はトレースと発散がなく重力波の自由度に対応する。上の式は重力波の膨張宇
宙における波動方程式となっている。
次にベクトル型摂動の運動方程式も上に導いたように
 成分と
成分と
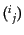 成分はそのままゲージ不変である。エネルギー運動量テンソルの
ベクトル型成分は
成分はそのままゲージ不変である。エネルギー運動量テンソルの
ベクトル型成分は
| |
|
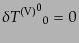 |
(J.4.130) |
| |
|
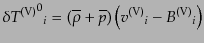 |
(J.4.131) |
| |
|
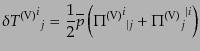 |
(J.4.132) |
となる。ここで、3次元速度場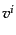 はゲージ不変ではなく、その変換を計算
すると、
はゲージ不変ではなく、その変換を計算
すると、
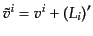 |
(J.4.133) |
となる.これは,空間座標のとり方が時間的に変化することによって,速度が
変わってしまうことを意味する.ベクトル型摂動に対して確かに式
(10.4.132)はゲージ不変である。そこで、ゲージ不変なベクトル型3次
元速度場を
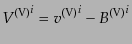 |
(J.4.134) |
で定義する。このゲージ不変量は時間一定面の慣性系からみた物質の速度に対
応する。実際、時間一定面に垂直な単位法ベクトルは摂動の一次までで、
| |
|
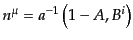 |
(J.4.135) |
| |
|
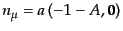 |
(J.4.136) |
となるから、
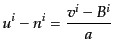 |
(J.4.137) |
となり、最後の式は時間一定面の座標点の速度に相対的な物質の速度に対応し
ている。このゲージ不変な速度を用いて、ベクトル型摂動の運動方程式
(10.4.91)および(10.4.92)は
| |
|
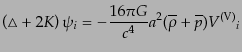 |
(J.4.138) |
| |
|
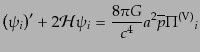 |
(J.4.139) |
となる。さらに、この方程式からポテンシャル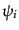 を消去すると、
を消去すると、
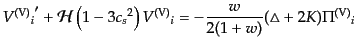 |
(J.4.140) |
という式が導かれる。
最後にスカラー型摂動の運動方程式を求める。密度ゆらぎ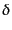 、速度ベク
トルのスカラー型成分
、速度ベク
トルのスカラー型成分
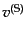 、圧力のゆらぎ
、圧力のゆらぎ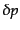 のゲージ変換は
のゲージ変換は
| |
|
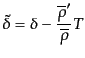 |
(J.4.141) |
| |
|
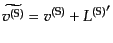 |
(J.4.142) |
| |
|
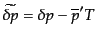 |
(J.4.143) |
となる。これより,密度ゆらぎや圧力は時間一定面のとり方による不定性があ
ることがわかる.ここで、ゲージ不変量を次のように定義する。
| |
|
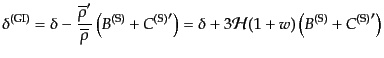 |
(J.4.144) |
| |
|
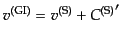 |
(J.4.145) |
| |
|
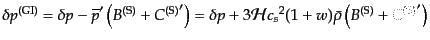 |
(J.4.146) |
すると、ゲージ不変なエネルギー運動量テンソル
(10.4.109)-(10.4.111)はこれらの量だけで書き表せて、
| |
|
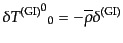 |
(J.4.147) |
| |
|
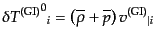 |
(J.4.148) |
| |
|
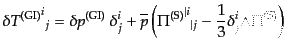 |
(J.4.149) |
となる。ここで,非等方ストレステンソルはトレースなしであることからスカ
ラー成分は一種類しかない.こうして,スカラー型摂動の運動方程式
(10.4.112)は
| |
|
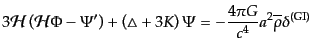 |
(J.4.150) |
| |
|
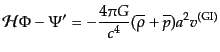 |
(J.4.151) |
| |
|
![$\displaystyle \triangle \Phi + (\triangle + 3K) \Psi
+ 3 \left[
2 {\cal H}'
+ {\cal H}^2
\right] \Phi$](img3193.png) |
|
| |
|
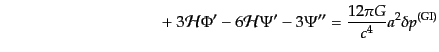 |
(J.4.152) |
| |
|
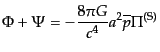 |
(J.4.153) |
となる。ここで、
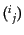 成分はトレース部分とトレースなしの部分に分
けることにより、最後の2つの式となる。
成分はトレース部分とトレースなしの部分に分
けることにより、最後の2つの式となる。
圧力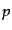 をエネルギー密度
をエネルギー密度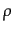 とバリオンあたりのエントロピー
とバリオンあたりのエントロピー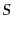 の関数と
考えて,状態方程式を
の関数と
考えて,状態方程式を
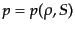 とすれば,このとき圧力のゆらぎはエ
ネルギー密度のゆらぎ
とすれば,このとき圧力のゆらぎはエ
ネルギー密度のゆらぎ
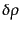 とエントロピーのゆらぎ
とエントロピーのゆらぎ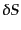 によ
り、
によ
り、
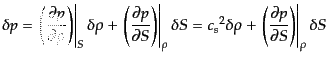 |
(J.4.154) |
と表される。そこで、エントロピーのゆらぎを表す量として、
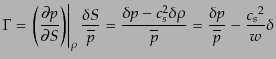 |
(J.4.155) |
を導入すれば、この量はゲージ不変量となっていることがすぐわかる.上の方
程式の組(10.4.151)-(10.4.154)を変形して,同値な方程式の組に
表すと便利である.式(10.4.151), (10.4.152) を時間微分したも
のを使えば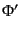 や
や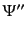 は消去され,背景時空の式
(10.4.72)-(10.4.74)を用いて変形すると,最終的に次の力
学的方程式
は消去され,背景時空の式
(10.4.72)-(10.4.74)を用いて変形すると,最終的に次の力
学的方程式
および、拘束の式
| |
|
![$\displaystyle \left(\triangle + 3K \right) \Psi
= - \frac32 {\cal H}^2 \Omega
\left[
\delta^{\rm (GI)} - 3 {\cal H}(1 + w) v^{\rm (GI)}
\right]$](img3206.png) |
(J.4.158) |
| |
|
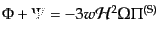 |
(J.4.159) |
が導かれる.最初の2式はニュートン近似の場合の線形化した連続の式および
オイラー方程式に良く似ていることがわかるだろう.力学的方程式
(10.4.157), (10.4.158)はエネルギー運動量保存則
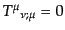 の内容に等しい.実際,左辺の摂動
の内容に等しい.実際,左辺の摂動
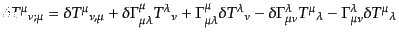 |
(J.4.160) |
を計算すると,時間成分 と空間成分
と空間成分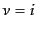 はそれぞれ次の2式となる.
はそれぞれ次の2式となる.
この式のスカラー成分をとってから,エネルギー運動量保存則
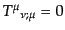 をゲージ不変量で書き直せば,式(10.4.157),
(10.4.158)に等価であることが確かめられる.
をゲージ不変量で書き直せば,式(10.4.157),
(10.4.158)に等価であることが確かめられる.
以上の式により、アインシュタイン方程式の摂動部の方程式がゲージ不変な形
に表せたが、物質のゆらぎについて他のゲージ不変量を使うこともある。例え
ば、式(10.4.159)は曲率項を除いて通常のポアソンの形をしているが、
この式のソース項を改めてゲージ不変な密度ゆらぎに取り直すこともできる:
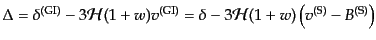 |
(J.4.163) |
この変数は,ゲージ不変摂動論を創始したバーディーンにより導入されたもの
で,バーディーンの変数という.ゲージ不変な速度はその
まま記号だけ変えて、
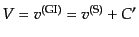 |
(J.4.164) |
と書いておこう。そして新しい変数
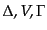 を
を
 の代わりに使うならば、方程式
(10.4.157)-(10.4.160)は多少簡単化して次のようになる。
の代わりに使うならば、方程式
(10.4.157)-(10.4.160)は多少簡単化して次のようになる。
| |
|
![$\displaystyle \Delta' - 3 w {\cal H}\Delta
= - \left(\triangle + 3K \right)
\left[ (1 + w) V - 2 w {\cal H}\Pi^{\rm (S)} \right]$](img3220.png) |
(J.4.165) |
| |
|
![$\displaystyle V' + {\cal H}V
= - \frac{{c_s}^2}{1 + w} \Delta - \Phi
- \frac{w}{1+w}
\left[
\Gamma + \frac23 (\triangle + 3K) \Pi^{\rm (S)}
\right]$](img3221.png) |
(J.4.166) |
| |
|
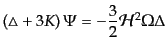 |
(J.4.167) |
| |
|
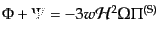 |
(J.4.168) |
この連立微分方程式においては,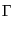 ,
, 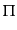 の形が与えられれば,
の形が与えられれば,
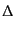 ,
, 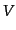 ,
, 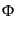 ,
,  について解けることになる.密度ゆらぎの成
長に対応する方程式として,上式から
について解けることになる.密度ゆらぎの成
長に対応する方程式として,上式から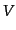 ,
, 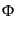 ,
,  を消去すること
により,
を消去すること
により,
と導ける.この式はエントロピーゆらぎと非等方ストレスが与えられたときに,
それらをソース項とする密度ゆらぎの二階常微分方程式になっている.これが
解ければ,その解を用いて
| |
|
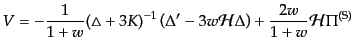 |
(J.4.170) |
| |
|
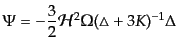 |
(J.4.171) |
| |
|
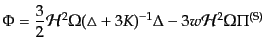 |
(J.4.172) |
と求まることになる.ここで,
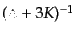 は演算子
は演算子
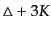 のグリーン関数を表している.
のグリーン関数を表している.
どのようなゲージ不変量を独立な変数として取るかには任意性がある.密度ゆ
らぎなどはゲージ依存する量なので,それらになるべく近い不変量を定義した
ものが
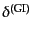 ,
, 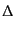 などである.以下に見るように,これ
らの不変量は特別なゲージのもとで実際の密度ゆらぎなどになっている.
などである.以下に見るように,これ
らの不変量は特別なゲージのもとで実際の密度ゆらぎなどになっている.
非等方ストレス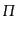 が無視できる場合にはアインシュタイン方程式
(10.4.151)-(10.4.154)は非常に簡単化する.この場合には式
(10.4.154)から明らかなように
が無視できる場合にはアインシュタイン方程式
(10.4.151)-(10.4.154)は非常に簡単化する.この場合には式
(10.4.154)から明らかなように
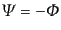 と表せるので1つのゲー
ジ不変ポテンシャルのみを用いればよく,その結果方程式の組は
と表せるので1つのゲー
ジ不変ポテンシャルのみを用いればよく,その結果方程式の組は
| |
|
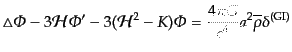 |
(J.4.173) |
| |
|
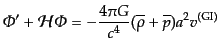 |
(J.4.174) |
| |
|
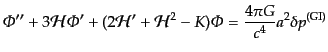 |
(J.4.175) |
となる.ここで,式(10.4.176)から式(10.4.174)の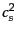 倍
を引くと
倍
を引くと
![$\displaystyle {\mit\Phi}'' + 3{\cal H}(1 + c_s^2){\mit\Phi}' - c_s^2 \triangle{...
...cal H}^2 - K)\right]{\mit\Phi}= \frac{4\pi G}{c^4} a^2\overline{p} {\mit\Gamma}$](img3242.png) |
(J.4.176) |
となり,エントロピーゆらぎをソースとするゲージ不変ポテンシャルの発展方
程式が得られる.





次へ: いくつかのゲージ固定との関係
上へ: 相対論的摂動論
前へ: ゲージ変換とスカラー・ベクトル・テンソル分解
目次
索引
All rights reserved © T.Matsubara 2004-2010
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11
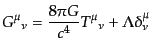
![]() については式(10.3.62)により、
それ自身ゲージ不変である。これはもともと座標変換の自由度であるゲージ変
換にはテンソル型の成分は含まれていないからである。アインシュタインテン
ソルの摂動部分について、テンソル型摂動の寄与を取り出すと次のようになる。
については式(10.3.62)により、
それ自身ゲージ不変である。これはもともと座標変換の自由度であるゲージ変
換にはテンソル型の成分は含まれていないからである。アインシュタインテン
ソルの摂動部分について、テンソル型摂動の寄与を取り出すと次のようになる。
![]() を考える。これら
はゲージに依存するので、ゲージ自由度を含まないような線形な組合せとして
を考える。これら
はゲージに依存するので、ゲージ自由度を含まないような線形な組合せとして
![]() および
および
![]() の2つなの
で、4つあるスカラー摂動のうち、物理的自由度は2つである。これは、ゲー
ジ変換を受けないような線形結合を作ることにより取り出すことができる。そ
のような組合せのうち、もっとも簡単なものは次のようなものである。
の2つなの
で、4つあるスカラー摂動のうち、物理的自由度は2つである。これは、ゲー
ジ変換を受けないような線形結合を作ることにより取り出すことができる。そ
のような組合せのうち、もっとも簡単なものは次のようなものである。
![]() を消去すれば、
を消去すれば、
![]() を次のように構成する。
を次のように構成する。
![]() によ
り自由度は3である。この3つの自由度を空間的速度
によ
り自由度は3である。この3つの自由度を空間的速度
![]() に取る。
非摂動時空では等方
に取る。
非摂動時空では等方
![]() であるから、
であるから、![]() は摂動の
1次の量である。この自由度により、一次までのオーダーで
は摂動の
1次の量である。この自由度により、一次までのオーダーで
![]() 成分と
成分と
![]() 成分はそのままゲージ不変である。エネルギー運動量テンソルの
ベクトル型成分は
成分はそのままゲージ不変である。エネルギー運動量テンソルの
ベクトル型成分は
![]() 、速度ベク
トルのスカラー型成分
、速度ベク
トルのスカラー型成分
![]() 、圧力のゆらぎ
、圧力のゆらぎ![]() のゲージ変換は
のゲージ変換は
![]() をエネルギー密度
をエネルギー密度![]() とバリオンあたりのエントロピー
とバリオンあたりのエントロピー![]() の関数と
考えて,状態方程式を
の関数と
考えて,状態方程式を
![]() とすれば,このとき圧力のゆらぎはエ
ネルギー密度のゆらぎ
とすれば,このとき圧力のゆらぎはエ
ネルギー密度のゆらぎ
![]() とエントロピーのゆらぎ
とエントロピーのゆらぎ![]() によ
り、
によ
り、
![]() ,
, ![]() などである.以下に見るように,これ
らの不変量は特別なゲージのもとで実際の密度ゆらぎなどになっている.
などである.以下に見るように,これ
らの不変量は特別なゲージのもとで実際の密度ゆらぎなどになっている.
![]() が無視できる場合にはアインシュタイン方程式
(10.4.151)-(10.4.154)は非常に簡単化する.この場合には式
(10.4.154)から明らかなように
が無視できる場合にはアインシュタイン方程式
(10.4.151)-(10.4.154)は非常に簡単化する.この場合には式
(10.4.154)から明らかなように
![]() と表せるので1つのゲー
ジ不変ポテンシャルのみを用いればよく,その結果方程式の組は
と表せるので1つのゲー
ジ不変ポテンシャルのみを用いればよく,その結果方程式の組は
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11