




次へ: 多成分流体
上へ: 相対論的摂動論
前へ: いくつかのゲージ固定との関係
目次
索引
曲率ゆらぎ
共動ゲージにおける空間計量の等方なゆらぎ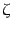 は応用上有用な量である.
このゆらぎを曲率ゆらぎ (curvature perturbation)と呼ぶ.このゆら
ぎが有用である理由のひとつは以下にみるように,ホライズンよりも大きなス
ケールで時間的に一定にとどまる場合があるという性質があるからである.共
動ゲージの変数
は応用上有用な量である.
このゆらぎを曲率ゆらぎ (curvature perturbation)と呼ぶ.このゆら
ぎが有用である理由のひとつは以下にみるように,ホライズンよりも大きなス
ケールで時間的に一定にとどまる場合があるという性質があるからである.共
動ゲージの変数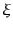 ,
, 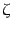 は,関係式(10.5.196),
(10.5.197)を定義と考えればゲージ不変量とみなすことができる.ア
インシュタイン方程式(10.4.152)を用いると曲率ゆらぎは
は,関係式(10.5.196),
(10.5.197)を定義と考えればゲージ不変量とみなすことができる.ア
インシュタイン方程式(10.4.152)を用いると曲率ゆらぎは
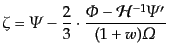 |
(J.6.197) |
と,ゲージ不変ポテンシャルだけで表される.式(10.5.196),
(10.5.197)から求めたゲージ不変ポテンシャルををアインシュタイン
方程式(10.4.152)に代入して式(10.4.82)を使えば,曲率ゆらぎ
に対する時間発展は
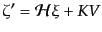 |
(J.6.198) |
となる.さらに式(10.4.167)を用いることによりこの式は
![$\displaystyle \zeta' = - \frac{\cal H}{1 + w} \left[ {c_{\rm s}}^2 \Delta + w {\mit\Gamma}+ \frac{2w}{3} \left(\triangle + 3K\right){\mit\Pi} \right] + KV$](img3291.png) |
(J.6.199) |
と表されることになる.
ここで,宇宙初期などで曲率と宇宙項が無視できる場合を考えると
 |
(J.6.200) |
である.また,式(10.6.200)の右辺の各項が第一項の密度ゆらぎと同
程度かそれ以下のオーダーであると仮定するJ1.
このとき,式(10.6.200)は
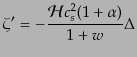 |
(J.6.201) |
となる.ただし,
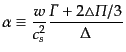 |
(J.6.202) |
はオーダー1以下と仮定された量である.この式はアインシュタイン方程式
(10.4.168)を使えば,
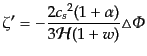 |
(J.6.203) |
となる.ゆらぎを平面波展開してその波数を とするとラプラシアンは
とするとラプラシアンは
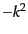 で置き換えられる.したがって,そのような平面波モードに対して
で置き換えられる.したがって,そのような平面波モードに対して
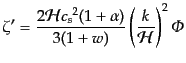 |
(J.6.204) |
となるので,超ハッブルスケール
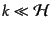 (
(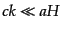 )では曲率ゆら
ぎは成長できないことがわかる.すなわち曲率ゆらぎは時間的に一定に保たれ
るため,方程式を解く必要がなく超ハッブルスケールのゆらぎの振舞いを調べ
るのに便利な量である.
)では曲率ゆら
ぎは成長できないことがわかる.すなわち曲率ゆらぎは時間的に一定に保たれ
るため,方程式を解く必要がなく超ハッブルスケールのゆらぎの振舞いを調べ
るのに便利な量である.
Footnotes
- ...
程度かそれ以下のオーダーであると仮定するJ1
- 通常非等方ストレスは
十分小さく,初期ゆらぎがのちに述べる断熱ゆらぎの場合にはこの仮定は成
り立っている.一方、等曲率ゆらぎの場合には超ホライズンスケールで
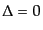 となるため、上の仮定を満たさず以下の議論が成り立たないので,
一般に曲率ゆらぎは保存しない.
となるため、上の仮定を満たさず以下の議論が成り立たないので,
一般に曲率ゆらぎは保存しない.





次へ: 多成分流体
上へ: 相対論的摂動論
前へ: いくつかのゲージ固定との関係
目次
索引
All rights reserved © T.Matsubara 2004-2010
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11
![]() は応用上有用な量である.
このゆらぎを曲率ゆらぎ (curvature perturbation)と呼ぶ.このゆら
ぎが有用である理由のひとつは以下にみるように,ホライズンよりも大きなス
ケールで時間的に一定にとどまる場合があるという性質があるからである.共
動ゲージの変数
は応用上有用な量である.
このゆらぎを曲率ゆらぎ (curvature perturbation)と呼ぶ.このゆら
ぎが有用である理由のひとつは以下にみるように,ホライズンよりも大きなス
ケールで時間的に一定にとどまる場合があるという性質があるからである.共
動ゲージの変数![]() ,
, ![]() は,関係式(10.5.196),
(10.5.197)を定義と考えればゲージ不変量とみなすことができる.ア
インシュタイン方程式(10.4.152)を用いると曲率ゆらぎは
は,関係式(10.5.196),
(10.5.197)を定義と考えればゲージ不変量とみなすことができる.ア
インシュタイン方程式(10.4.152)を用いると曲率ゆらぎは
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11