




次へ: 線形ボルツマン方程式
上へ: 相対論的摂動論
前へ: 曲率ゆらぎ
目次
索引
Subsections
ここまでは,宇宙の全体としてのエネルギー運動量テンソル
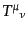 を
用いた。宇宙の中のエネルギー形態がいくつかの種類に分けられる場合、この
エネルギー運動量テンソルはそれらの種類
を
用いた。宇宙の中のエネルギー形態がいくつかの種類に分けられる場合、この
エネルギー運動量テンソルはそれらの種類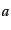 ごとの成分の和
ごとの成分の和
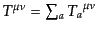 で与えられる。これは,式
(10.4.119)-(10.4.126)により非摂動量について
で与えられる。これは,式
(10.4.119)-(10.4.126)により非摂動量について
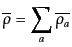 |
|
|
(J.7.205) |
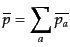 |
|
|
(J.7.206) |
となる.各成分について,圧力と密度の比
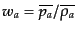 お
よび音速
お
よび音速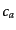 は,
は,
| |
|
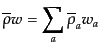 |
(J.7.207) |
| |
|
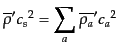 |
(J.7.208) |
である。摂動量に対してはゲージ依存する変数について
| |
|
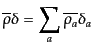 |
(J.7.209) |
| |
|
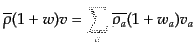 |
(J.7.210) |
| |
|
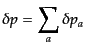 |
(J.7.211) |
| |
|
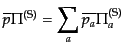 |
(J.7.212) |
となることがわかる。したがって,エントロピーのゆらぎは
![$\displaystyle \overline{p}\Gamma = \sum_a \left[ \overline{p_a} \Gamma_a + \left({c_a}^2 - {c_s}^2\right) \overline{\rho_a} \delta_a \right]$](img3311.png) |
(J.7.213) |
と計算される.ここで,エントロピーゆらぎの各成分 は
は
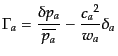 |
(J.7.214) |
である.多成分系では成分ごとのエントロピーにゆらぎがなくても成分間で
音速の異なる場合には全体のエントロピーにゆらぎが生じ得ることがわかる.
各々の成分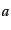 がお互いに相互作用している場合,成分ごとのゆらぎを取り扱
うには,各成分間でのエネルギー・運動量の交換を記述する輸送方程式が必要
になる.そのような場合は後に取り扱うことにして,ここでは,成分間の直接
の相互作用が無視できる場合を考えよう.すなわち,重力のみを通して各成分
のゆらぎが影響しあう場合を考える.各成分
がお互いに相互作用している場合,成分ごとのゆらぎを取り扱
うには,各成分間でのエネルギー・運動量の交換を記述する輸送方程式が必要
になる.そのような場合は後に取り扱うことにして,ここでは,成分間の直接
の相互作用が無視できる場合を考えよう.すなわち,重力のみを通して各成分
のゆらぎが影響しあう場合を考える.各成分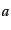 のエネルギー運動量テンソル
のエネルギー運動量テンソル
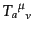 は,独立に保存則
は,独立に保存則
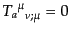 を満たす.
背景場についてこれは,
を満たす.
背景場についてこれは,
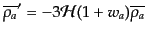 |
(J.7.215) |
あるいは,
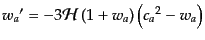 |
(J.7.216) |
となる.
さらに,線形摂動
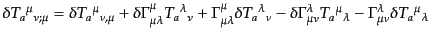 |
(J.7.217) |
を計算すると,時間成分 と空間成分
と空間成分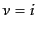 はそれぞれ次の2式となる.
はそれぞれ次の2式となる.
いま成分間にエネルギー・運動量の交換がなければ
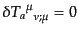 であるから,
であるから,
が成り立つ.
この2式にはテンソル型成分がないことは容易にわかる.また,ベクトル型は
第2式にのみ含まれている.背景場の3次元曲率テンソル(2.2.16)を
使って共変微分を交換することにより,恒等式
| |
|
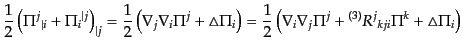 |
|
| |
|
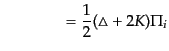 |
(J.7.222) |
が成り立つので,(10.7.222)のベクトル成分は
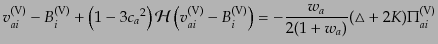 |
(J.7.223) |
である.ベクトル型のゲージ変換は成分ごとに
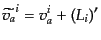 |
|
|
(J.7.224) |
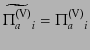 |
|
|
(J.7.225) |
であり,式(10.7.224)は確かにゲージ不変である.
したがって,ゲージ不変なベクトル型3次元速度場を式
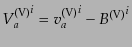 |
(J.7.226) |
で定義すれば,上の式はゲージ不変な形,
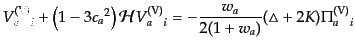 |
(J.7.227) |
となる.これは1成分の場合には式(10.4.141)に等しい.
式(10.7.221), (10.7.222)のスカラー成分も同様に求まる.非等方
ストレスはトレースレスであるから,スカラー成分について,
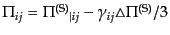 となる.
以下,スカラー量を表す(S)は省略する.再び3次元共変微分の交換則を用い
ることにより,
となる.
以下,スカラー量を表す(S)は省略する.再び3次元共変微分の交換則を用い
ることにより,
となる.スカラー成分のゲージ変換は成分ごとに
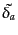 |
 |
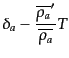 |
(J.7.230) |
 |
 |
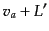 |
(J.7.231) |
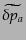 |
 |
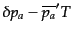 |
(J.7.232) |
となる.したがって,多成分の場合も はゲージ不変であり,また,
エントロピーゆらぎを引き起こす量
はゲージ不変であり,また,
エントロピーゆらぎを引き起こす量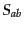 もまたゲージ不変である.そこで,
1成分の場合にならって成分ごとのゲージ不変量を次のように定義する.
もまたゲージ不変である.そこで,
1成分の場合にならって成分ごとのゲージ不変量を次のように定義する.
ただし,式(10.7.234)の2番目の等式では背景場にエネルギー運動量輸
送のない場合の保存則(10.7.216)を用いた.これにより保存則
(10.7.229), (10.7.230) を書き換えると,
というゲージ不変な形になる.これは,単成分の場合,式(10.4.157)お
よび(10.4.158)に等しいことがわかる.拘束の式(10.4.168),
(10.4.169)は全体の運動量・エネルギーテンソルに対するアインシュタ
イン方程式であるから,
と書ける.
上に導入したゲージ不変量
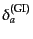 ,
,
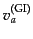 は共形
ニュートンゲージで見たゆらぎに対応する量であるが, 共動ゲージで見たゆら
ぎに対応するゲージ不変量は全物質の平均速度によって,
は共形
ニュートンゲージで見たゆらぎに対応する量であるが, 共動ゲージで見たゆら
ぎに対応するゲージ不変量は全物質の平均速度によって,
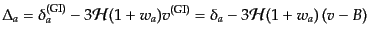 |
(J.7.239) |
により定義される量である.
多成分系において,背景場にエネルギー輸送がない場合,式(10.7.216)か
ら音速とエントロピーのゆらぎの式(10.7.208), (10.7.209)は
| |
|
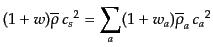 |
(J.7.240) |
| |
|
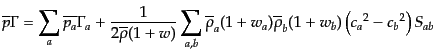 |
(J.7.241) |
となる.ここで,
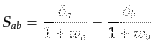 |
(J.7.242) |
である.音速の異なる成分の混ざった系では,各成分のエントロピーゆらぎ
 に加えて,ゆらぎの差で表される量
に加えて,ゆらぎの差で表される量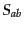 が全体のエントロピー
ゆらぎに寄与することになる.
が全体のエントロピー
ゆらぎに寄与することになる.
成分間の相互作用のない場合にはエントロピーゆらぎに寄与する量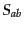 の
発展方程式は極めてシンプルである.実際,それは式(10.7.229) から容
易に導けて,
の
発展方程式は極めてシンプルである.実際,それは式(10.7.229) から容
易に導けて,
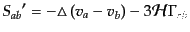 |
(J.7.243) |
となる.ただし,
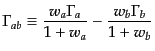 |
(J.7.244) |
を用いた.速度の差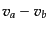 はゲージ不変であり,式(10.7.244)はそ
のままゲージ不変な式になっている.こうして,成分間の速度差
はゲージ不変であり,式(10.7.244)はそ
のままゲージ不変な式になっている.こうして,成分間の速度差
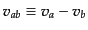 がエントロピー摂動の発展を決めていることがわかる.し
たがって,速度差についての発展についての方程式を導いておくと便利である.
式(10.7.230)において,成分
がエントロピー摂動の発展を決めていることがわかる.し
たがって,速度差についての発展についての方程式を導いておくと便利である.
式(10.7.230)において,成分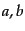 について差をとると,
について差をとると,
という式が導ける.ここで,
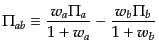 |
(J.7.246) |
である.また,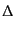 は式(10.4.164)で与えられる全物質についてのバー
ディーン変数である.式(10.7.246)の証明には,次の恒等式を用いるとよ
い:
は式(10.4.164)で与えられる全物質についてのバー
ディーン変数である.式(10.7.246)の証明には,次の恒等式を用いるとよ
い:
| |
|
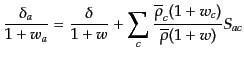 |
(J.7.247) |
| |
|
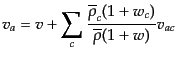 |
(J.7.248) |
式(10.7.246)はそのままゲージ不変であることが明らかである.





次へ: 線形ボルツマン方程式
上へ: 相対論的摂動論
前へ: 曲率ゆらぎ
目次
索引
All rights reserved © T.Matsubara 2004-2010
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11
![]() を
用いた。宇宙の中のエネルギー形態がいくつかの種類に分けられる場合、この
エネルギー運動量テンソルはそれらの種類
を
用いた。宇宙の中のエネルギー形態がいくつかの種類に分けられる場合、この
エネルギー運動量テンソルはそれらの種類![]() ごとの成分の和
ごとの成分の和
![]() で与えられる。これは,式
(10.4.119)-(10.4.126)により非摂動量について
で与えられる。これは,式
(10.4.119)-(10.4.126)により非摂動量について
![]() がお互いに相互作用している場合,成分ごとのゆらぎを取り扱
うには,各成分間でのエネルギー・運動量の交換を記述する輸送方程式が必要
になる.そのような場合は後に取り扱うことにして,ここでは,成分間の直接
の相互作用が無視できる場合を考えよう.すなわち,重力のみを通して各成分
のゆらぎが影響しあう場合を考える.各成分
がお互いに相互作用している場合,成分ごとのゆらぎを取り扱
うには,各成分間でのエネルギー・運動量の交換を記述する輸送方程式が必要
になる.そのような場合は後に取り扱うことにして,ここでは,成分間の直接
の相互作用が無視できる場合を考えよう.すなわち,重力のみを通して各成分
のゆらぎが影響しあう場合を考える.各成分![]() のエネルギー運動量テンソル
のエネルギー運動量テンソル
![]() は,独立に保存則
は,独立に保存則
![]() を満たす.
背景場についてこれは,
を満たす.
背景場についてこれは,
![]() となる.
以下,スカラー量を表す(S)は省略する.再び3次元共変微分の交換則を用い
ることにより,
となる.
以下,スカラー量を表す(S)は省略する.再び3次元共変微分の交換則を用い
ることにより,
![]() ,
,
![]() は共形
ニュートンゲージで見たゆらぎに対応する量であるが, 共動ゲージで見たゆら
ぎに対応するゲージ不変量は全物質の平均速度によって,
は共形
ニュートンゲージで見たゆらぎに対応する量であるが, 共動ゲージで見たゆら
ぎに対応するゲージ不変量は全物質の平均速度によって,
![]() の
発展方程式は極めてシンプルである.実際,それは式(10.7.229) から容
易に導けて,
の
発展方程式は極めてシンプルである.実際,それは式(10.7.229) から容
易に導けて,
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11