




次へ: 自由場の量子化
上へ: 場の量子化と粒子の相互作用
前へ: 相対論的に可能な場
目次
索引
Subsections
もっとも簡単な場として、まずは実スカラー場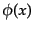 を考える。ここで、
を考える。ここで、
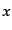 は時空座標
は時空座標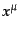 を省略して表している。実スカラー場の場合,場の時
間微分について2次で、かつ場の1階微分までしか含まないローレンツ不変な
ラグランジアン密度としては,次の形しかないことがわかる:
を省略して表している。実スカラー場の場合,場の時
間微分について2次で、かつ場の1階微分までしか含まないローレンツ不変な
ラグランジアン密度としては,次の形しかないことがわかる:
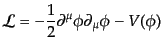 |
(H.4.99) |
運動項に場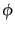 の任意関数がかかったものの方が一般性があるように見える
かもしれないが、そのような場合でも、場を再定義すれば上の形に帰着できる。
ここで,
の任意関数がかかったものの方が一般性があるように見える
かもしれないが、そのような場合でも、場を再定義すれば上の形に帰着できる。
ここで,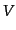 はポテンシャルに対応する.すると、場の方程式は,
はポテンシャルに対応する.すると、場の方程式は,
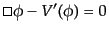 |
(H.4.100) |
となる.ここで、
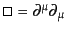 はダランベルシア
ンである。
はダランベルシア
ンである。
運動方程式が場について線形方程式になるような場を自由場 (free
field)という。いまの場合、ポテンシャル項が2次式
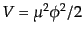 であれば自由場となる。その場合ラグランジアン密度は、
であれば自由場となる。その場合ラグランジアン密度は、
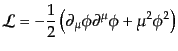 |
(H.4.101) |
である。これに対して、3次以上のポテンシャル項がある場合は相互作用があ
る場合に対応する。自由場の場合、運動方程式は、
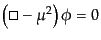 |
(H.4.102) |
となる。この方程式は、クライン・ゴルドン方程式(Klein-Gordon
equation)と呼ばれる。この方程式は、4元運動量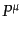 と質量
と質量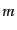 に対する
アインシュタインの関係
に対する
アインシュタインの関係
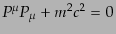 において、非相対論的
シュレーディンガー方程式を構成する時の量子化規則
において、非相対論的
シュレーディンガー方程式を構成する時の量子化規則
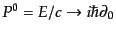 ,
,
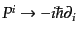 を適用した微分
方程式になっている。この対応では、質量
を適用した微分
方程式になっている。この対応では、質量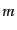 とパラメータ
とパラメータ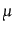 は、
は、
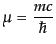 |
(H.4.103) |
と関係している。だがシュレーディンガー方程式の場合は時間について1階微
分しか含まないために、粒子を見つける全確率が保存していたのに対し、クラ
イン・ゴルドン方程式の場合には、時間に2階微分を含み、全確率が保存しな
くなる。つまり、この方程式で表される場を量子力学的波動関数と考えると、
意味のないものとなる。したがってこの場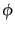 は通常の波動関数と考えるこ
とはできず、さらなる量子化の対象となるべき古典場と見なされる。
は通常の波動関数と考えるこ
とはできず、さらなる量子化の対象となるべき古典場と見なされる。
自由場のラグランジアンに場の2次形式でない項を付け加えると相互作用をす
る系を表すことになる。実スカラー場については最も簡単な自己相互作用の例
の一つとして、
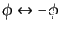 の対称性を持つ
の対称性を持つ
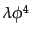 モデルがある。そのラグランジアン密度は
モデルがある。そのラグランジアン密度は
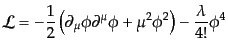 |
(H.4.104) |
で与えられ、その運動方程式は
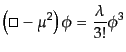 |
(H.4.105) |
となる。
自由場のクライン・ゴルドン方程式(8.4.102)に戻り、これをフーリエ
変換
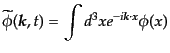 |
(H.4.106) |
により解こう。フーリエ係数に対する方程式は
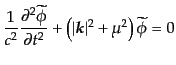 |
(H.4.107) |
となるが、これは調和振動子の方程式と同じで、ただちに一般解が、
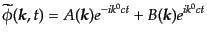 |
(H.4.108) |
と求まる。ただし、
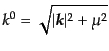 |
(H.4.109) |
である。ここで、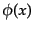 は実数であることから、
は実数であることから、
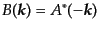 でなければならないことがわかる。すると、式
(8.4.106)の逆変換により、
でなければならないことがわかる。すると、式
(8.4.106)の逆変換により、
![$\displaystyle \phi(x) = \int \frac{d^3k}{(2\pi)^3} \left[A({\mbox{\boldmath$k$}}) e^{ikx} + A^*({\mbox{\boldmath$k$}}) e^{-ikx} \right]$](img1632.png) |
(H.4.110) |
がクライン・ゴルドン方程式の一般解である。ここで、
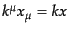 と
略記している。
と
略記している。
この一般解の形(8.4.110)は、基本モード
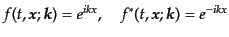 |
(H.4.111) |
の重ね合わせで表されている。前者は正振動モード(positive frequency
mode), 後者は負振動モード(negative frequency mode)と呼ばれ、各々時間
微分演算子の固有関数となっている:
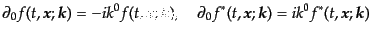 |
(H.4.112) |
また、場のスカラー積をあるローレンツ系での時刻一定面における積分として、
![$\displaystyle (\phi_1,\phi_2) = -i \int d^3x \left. \left\{ \phi_1(x)[\partial_...
...i_2^*(x)] - [\partial_0 \phi_1(x)] \phi_2^*(x) \right\} \right\vert _{x_0 = ct}$](img1636.png) |
(H.4.113) |
で定義すると、このスカラー積について基本モードは直交し、
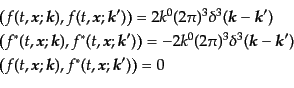 |
(H.4.114) |
を満たすことがわかる。いまの例では平面波によって基本モードを表している
が、基本モードの選び方は一意的ではなく、フーリエ・ベッセル級数などによっ
て展開してもかまわない。また、一般にミンコフスキー時空でない場合には平
面波展開は使えず、背景時空に応じて適切な基本モードを場の方程式の解の完
全系から求める必要があることを注意しておく。
さて、式(8.4.110)に戻り、
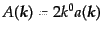 とおけば、
とおけば、
![$\displaystyle \phi(x) = \int \frac{d^3k}{(2\pi)^3 2k^0} \left[a({\mbox{\boldmath$k$}}) e^{ikx} + a^*({\mbox{\boldmath$k$}}) e^{-ikx} \right]$](img1639.png) |
(H.4.115) |
と書き表される。ここで、現れてきた積分測度はローレンツ不変である。事実、
エネルギーはローレンツ変換で符合を変えないことと、
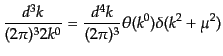 |
(H.4.116) |
であることから明らかである。
ラグランジアンに虚数部があるとエネルギーが実数でなくなるので、ラグラン
ジアン密度は実でなければならない。そこで、自由複素スカラー場
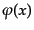 のラグランジアン密度としては
のラグランジアン密度としては
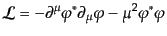 |
(H.4.117) |
というものになる。この場合にも運動方程式はクライン・ゴルドン方程式
(8.4.102)となる。この複素スカラー場には対称性があり、次の位相変
換
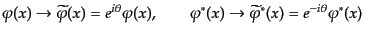 |
(H.4.118) |
についてラグランジアン密度が不変である。すると、ネーターの定理が適用で
きて保存量が存在する。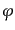 ,
, 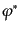 を独立変数と考えると、この
場合式(8.1.9), (8.1.10)において、
を独立変数と考えると、この
場合式(8.1.9), (8.1.10)において、
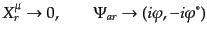 |
(H.4.119) |
と対応し、ネーターカレントは
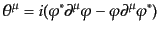 |
(H.4.120) |
となる。これに対応する保存量は
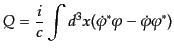 |
(H.4.121) |
である。この保存量は電荷に対応するものであり、複素スカラー場は電荷を帯
びた粒子の記述になっている。これに対して実スカラー場にはこのような保存
量はなく、中性粒子を記述するものになっていることがわかる。
複素スカラー場に対するクライン・ゴルドン方程式を基本モードは実スカラー
場のものと同じであるが、場が実でないことからその解の運動量表示は
![$\displaystyle \varphi(x) = \int \frac{d^3k}{(2\pi)^3 2k^0} \left[a({\mbox{\boldmath$k$}}) e^{ikx} + b^*({\mbox{\boldmath$k$}}) e^{-ikx} \right]$](img1649.png) |
(H.4.122) |
となり、正振動モードと負振動モードにそれぞれ自由度がある。
次に、自由スピノル場からなる系を考えてみよう。そのラグランジアンにおい
て、運動項は場の微分を含んだ実のスカラー量である。スピノルはベクトルの
添字を持たないので、微分演算子
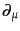 からスカラー量を作るために、
式(8.3.90)で導入された
からスカラー量を作るために、
式(8.3.90)で導入された
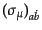 ,
,
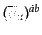 を利用すればよい。すると、
を利用すればよい。すると、
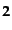 スピ
ノル
スピ
ノル
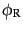 からつくるローレンツ不変な組み合わせとして、
からつくるローレンツ不変な組み合わせとして、
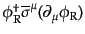 と
いうものが考えられる。この形のままでは実数ではないので複素共役を使って
実数にする。
と
いうものが考えられる。この形のままでは実数ではないので複素共役を使って
実数にする。
ただし、実は、量子論ではスピノル場はフェルミ粒子を表す場になるため、対
応する古典論を考えるときには通常の数ではなく、グラスマン数
(Grassmann number) というもので表されなければならないことが知られてい
る。グラスマン数とは、お互いに反交換するような数である。例えば、2つの
グラスマン数
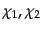 は、
は、
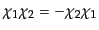 |
(H.4.123) |
を満たす。グラスマン数と通常の数は普通に交換する。グラスマン数の積の複
素共役は、
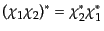 |
(H.4.124) |
であることが示せる。
スピノル場をグラスマン数であるとすると、全微分とならず、かつ実数となる
形として、
![$\displaystyle {\cal L}_{\rm R}^{\rm kin} = -\frac{i}{2} \left[ \phi_{\rm R}^\da...
...- (\partial_\mu \phi_{\rm R}^\dagger) \overline{\sigma}^\mu \phi_{\rm R}\right]$](img1656.png) |
(H.4.125) |
という形がラグランジアンの運動項としてつくれる。パウリ行列が
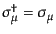 ,
,
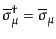 を満たすことと、スピノルがグラスマン数であること
に注意すれば、ここにつくった量は実数であることが確かめられる。同様に、
を満たすことと、スピノルがグラスマン数であること
に注意すれば、ここにつくった量は実数であることが確かめられる。同様に、
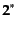 スピノル
スピノル
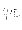 の場合の運動項は、
の場合の運動項は、
![$\displaystyle {\cal L}_{\rm L}^{\rm kin} = -\frac{i}{2} \left[ \phi_{\rm L}^\da...
...i_{\rm L}) - (\partial_\mu \phi_{\rm L}^\dagger) \sigma^\mu \phi_{\rm L}\right]$](img1660.png) |
(H.4.126) |
とすればよい。ただし、2成分スピノルの添字の位置は、
 スピノルの
場合、
スピノルの
場合、
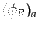 、
、
 スピノルの場合、
スピノルの場合、
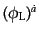 をそれぞれの標準位置とし、パウリ行列については
(8.3.90)の標準位置を使っている。
をそれぞれの標準位置とし、パウリ行列については
(8.3.90)の標準位置を使っている。
ここで、各々のラグランジアンは空間反転に対する不変性、すなわちパリティ
不変性を破っている。事実、空間反転に対してローレンツ群の生成子
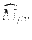 は空間反転に対して、
は空間反転に対して、
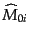 は空間の添字が一つ
なので符合を変え、
は空間の添字が一つ
なので符合を変え、
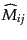 は符合を変えない。すると、式
(8.3.64), (8.3.65)より、生成子
は符合を変えない。すると、式
(8.3.64), (8.3.65)より、生成子
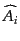 と
と
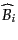 がお互いに入れ替わることになり、
がお互いに入れ替わることになり、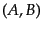 表現は
表現は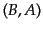 表現に
なる。これは空間反転について、
表現に
なる。これは空間反転について、
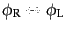 、すなわち、
、すなわち、
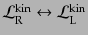 と入れ替わることを意味する。2つのスピノルを区別す
るR, Lは、この性質を反映し、
と入れ替わることを意味する。2つのスピノルを区別す
るR, Lは、この性質を反映し、
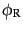 は右手系のスピノル、
は右手系のスピノル、
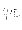 は左手系のスピノルと考えることを表しているのである。どち
らかが左または右である必然性はなく、単に便宜的に決っているだけである。
は左手系のスピノルと考えることを表しているのである。どち
らかが左または右である必然性はなく、単に便宜的に決っているだけである。
したがって、もしパリティ不変性を保ちたければ、これらの2つのラグラン
ジアンを足し合わせておけばよい:
![$\displaystyle {\cal L}^{\rm kin}_{\rm Dirac} = {\cal L}^{\rm kin}_{\rm R} + {\c...
...mu (\partial_\mu \psi) - (\partial_\mu \overline{\psi}) \gamma^\mu \psi \right]$](img1669.png) |
(H.4.127) |
ここで、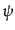 は4成分スピノルで、2つの2成分スピノルを組み合わせた
は4成分スピノルで、2つの2成分スピノルを組み合わせた
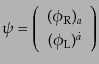 |
(H.4.128) |
で定義した。この4成分スピノルはディラックスピノル (Dirac spinor)
と呼ばれるものである。また、
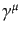 は
は 行列
行列
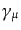 の添字を上げたもので、その定義は、
の添字を上げたもので、その定義は、
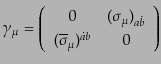 |
(H.4.129) |
すなわち、
 |
(H.4.130) |
である。さらに、
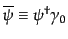 |
(H.4.131) |
はパウリ共役 (Pauli adjoint)と呼ばれるものである。
行列
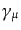 には次の関係がある:
には次の関係がある:
| |
|
![$\displaystyle [\gamma_\mu, \gamma_\nu]_+ =
\gamma_\mu \gamma_\nu + \gamma_\nu \gamma_\mu =
-2 \eta_{\mu\nu}$](img1677.png) |
(H.4.132) |
| |
|
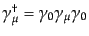 |
(H.4.133) |
次の 行列
行列
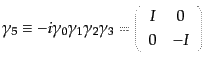 |
(H.4.134) |
を定義すると、行列
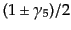 は4成分スピノルを左手系と右手系
に射影する射影行列となる。
は4成分スピノルを左手系と右手系
に射影する射影行列となる。
さて、
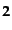 スピノルの複素共役は
スピノルの複素共役は
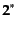 スピノルとなり、逆に
スピノルとなり、逆に
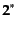 スピノルの複素共役は
スピノルの複素共役は
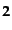 スピノルとなるので、ディラック
スピノル(8.4.128)からつくる
スピノルとなるので、ディラック
スピノル(8.4.128)からつくる
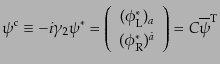 |
(H.4.135) |
もディラックスピノルの変換性をもつ。ここで、
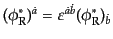 ,
,
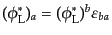 はスピノルの複素共役の添字をその変換性の標準
位置へもってきたものである。この変換を荷電共役 (charge
conjugation)と呼ぶ。この変換は
はスピノルの複素共役の添字をその変換性の標準
位置へもってきたものである。この変換を荷電共役 (charge
conjugation)と呼ぶ。この変換は
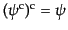 を満た
す。また、
を満た
す。また、
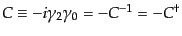 |
(H.4.136) |
は荷電共役行列と呼ばれ、
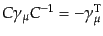 |
(H.4.137) |
を満たす。
パリティの不変性を要求しなければ右手系あるいは左手系のスピノルのみの系
を考えてもよい。このとき2成分スピノルを用いた式(8.4.125)または
(8.4.126)が運動項を与えるが、これらの場合でも4成分スピノルで表
示することも可能である。2成分の左手系スピノルと右手系スピノルから、
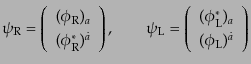 |
(H.4.138) |
によってディラックスピノルの変換をする4成分スピノルがつくれる。このよ
うな重複した表示はマヨラナスピノル (Majorana spinor)と呼ぶ。これ
に対してもとの2成分表示のスピノルはワイルスピノル (Weyl spinor)
と呼ぶ。マヨラナスピノルの荷電共役は自分自身に等しい:
 |
(H.4.139) |
2成分スピノルで書かれた運動項(8.4.125), (8.4.126)は、
マヨラナ表示では、
![$\displaystyle {\cal L}^{\rm kin}_{\rm R} =
-\frac{i}{4}
\left[
\overline{\p...
... R}) -
(\partial_\mu \overline{\psi}_{\rm R}) \gamma^\mu \psi_{\rm R}
\right]$](img1689.png) |
|
|
(H.4.140) |
![$\displaystyle {\cal L}^{\rm kin}_{\rm L} =
-\frac{i}{4}
\left[
\overline{\p...
... L}) -
(\partial_\mu \overline{\psi}_{\rm L}) \gamma^\mu \psi_{\rm L}
\right]$](img1690.png) |
|
|
(H.4.141) |
となる。
上に与えられたラグランジアンの運動項には次の位相変換
| |
|
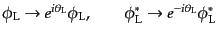 |
(H.4.142) |
| |
|
 |
(H.4.143) |
に対して不変であるという性質がある。これに対応し、ディラックスピノルに対
しては4成分全体の位相変換
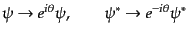 |
(H.4.144) |
および、カイラル変換 (chiral transformation)
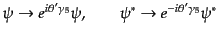 |
(H.4.145) |
について不変となる。マヨラナスピノル(8.4.138)については4成分全
体の位相変換にはできないが、カイラル変換については依然不変性を持つ。ラ
グランジアンが運動項のみからなる場合に、これら2種の不変性についてネー
ターの定理から不変カレントを求めると、全位相変換について
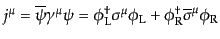 |
(H.4.146) |
カイラル変換について
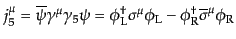 |
(H.4.147) |
となる。これより導かれる保存量は
| |
|
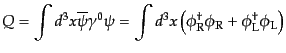 |
(H.4.148) |
| |
|
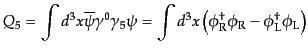 |
(H.4.149) |
である。
次に、場の微分を含まない質量項を考える。右手系スピノルのみでスカラーと
なる組み合わせは
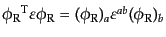 である。もし、スピノ
ルがグラスマン数でなければ
である。もし、スピノ
ルがグラスマン数でなければ
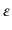 が反対称だからこの組み合わせは
ゼロになってしまうが、グラスマン数ゆえに、このような項が生き残れるので
ある。このことに注意して、複素共役との足し合わせにより実数をつくればそ
れが質量項となる。左手系も同様にして、
が反対称だからこの組み合わせは
ゼロになってしまうが、グラスマン数ゆえに、このような項が生き残れるので
ある。このことに注意して、複素共役との足し合わせにより実数をつくればそ
れが質量項となる。左手系も同様にして、
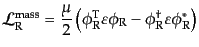 |
|
|
(H.4.150) |
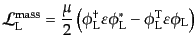 |
|
|
(H.4.151) |
というものができる.この質量項はマヨラナ質量項 (Majorana mass
term)と呼ばれるものであるH2。この質量項はそれぞれの位相変換(8.4.142),
(8.4.143)の不変性を破る。マヨラナスピノルで表し直すと、
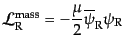 |
|
|
(H.4.152) |
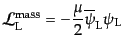 |
|
|
(H.4.153) |
となることがわかる。この項ももちろんカイラル不変性を破っている。
右手系と左手系のスピノルの両方を用いればもう一つ実の2次形式が作れて、
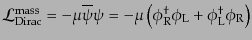 |
(H.4.154) |
という質量項ができる。これをディラック質量項 (Dirac mass term)と
いう。この質量項は全位相変換(8.4.144)の不変性を保つが、カイラル
不変性は破ってしまう。
以上の考察で、自由スピノル場のラグランジアンが構成できた。パリティ不変
性を破るラグランジアンとしては、左手系のマヨラナスピノルあるいはワイル
スピノルから、
 |
(H.4.155) |
が構成される。ただし、全微分の項は落とした。ここで、
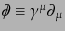 であり、スラッシュはガンマ行列によって
縮約する操作を表す。ニュートリノは左手系のスピノルしか確認されておらず、
実際にパリティが破れたフェルミオンであり、自由状態はこのラグランジアン
で記述することが可能である。マヨラナスピノルは4成分で書かれてはいるが、
実質2 成分だから4自由度しかなく、拘束条件(8.4.139)を考慮する必
要がある。また、パリティ不変性を保つラグランジアンは、ディラックスピノ
ルから構成され、
であり、スラッシュはガンマ行列によって
縮約する操作を表す。ニュートリノは左手系のスピノルしか確認されておらず、
実際にパリティが破れたフェルミオンであり、自由状態はこのラグランジアン
で記述することが可能である。マヨラナスピノルは4成分で書かれてはいるが、
実質2 成分だから4自由度しかなく、拘束条件(8.4.139)を考慮する必
要がある。また、パリティ不変性を保つラグランジアンは、ディラックスピノ
ルから構成され、
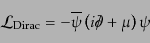 |
(H.4.156) |
となる。これは電子やクォークなど、パリティの破れていないフェルミオンを
表す自由ラグランジアンになっている。
自由ディラック場のラグランジアンから運動方程式を求めると、
 |
(H.4.157) |
となる。これはディラック方程式 (Dirac equation)であり、もともと
ディラックにより、非相対論的なシュレーディンガー方程式を相対論的に一般
化しつつ確率の保存する波動関数を導く方程式として提案されたものである。
事実、この方程式は時間微分について1階であることからシュレーディンガー
方程式のように保存する確率密度が定義できる。さらに、式(8.4.132)に
よって
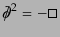 であることがわ
かるから、
であることがわ
かるから、
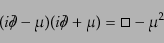 |
(H.4.158) |
であって、ディラックスピノルの各成分すべてがクライン・ゴルドン方程式を
満たすことがわかる。だが、場の量子論の立場からは、スピノル場は相対論的
に許される古典場の一種と見なされる。
スカラー場のときと同様に、この運動方程式の解の完全系を求めておこう。ス
ピノルの各成分がクライン・ゴルドン方程式を満たすことから、スカラー場の
平面波展開と同様の議論によって、
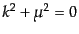 を満たす4元ベクトル
を満たす4元ベクトル
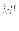 と4成分スピノル
と4成分スピノル
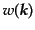 により、
により、
 という形を基本モードとしてもつことがわかる。ここで、
という形を基本モードとしてもつことがわかる。ここで、
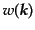 はそれぞれのモードについて
はそれぞれのモードについて
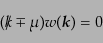 |
(H.4.159) |
を満たすが、この線形連立方程式を解くのは直線的である。その独立解は正振
動モードと負振動モードについて各2つずつある。それぞれの独立解を添字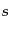 で区別することにして、正振動モードの解を
で区別することにして、正振動モードの解を
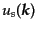 , 負振動モードの
解を
, 負振動モードの
解を
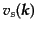 と表記することにする。具体的な解の形は以下では必要
ないのでここでは与えないが、求めることは難しくない。これらは、
と表記することにする。具体的な解の形は以下では必要
ないのでここでは与えないが、求めることは難しくない。これらは、
| |
|
 |
(H.4.160) |
| |
|
 |
(H.4.161) |
を満たす。各モードでの2つの独立解への分解の仕方は任意であるが、スピン
の2倍
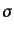 を運動量方向
を運動量方向
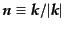 へ射
影する行列
へ射
影する行列
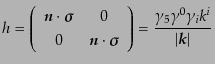 |
(H.4.162) |
の固有ベクトルへ分解したものがよく用いられる。この射影行列は
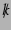 と交換することが確かめられるので、式(8.4.159)の縮退
した固有ベクトルを2つの直交ベクトルに分解できるのである。その固有値を
と交換することが確かめられるので、式(8.4.159)の縮退
した固有ベクトルを2つの直交ベクトルに分解できるのである。その固有値を
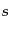 とすると、これはヘリシティ (helicity)と呼ばれる量であり、
とすると、これはヘリシティ (helicity)と呼ばれる量であり、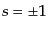 である。
である。
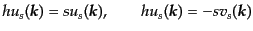 |
(H.4.163) |
他の分解をしてもよいが、いずれにしても次の直交規格化関
係を満たすように取ることにする:
| |
|
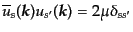 |
(H.4.164) |
| |
|
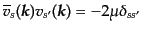 |
(H.4.165) |
ここで、
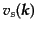 を決める式は
を決める式は
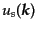 を決める式をすべて
を決める式をすべて
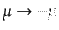 としたものであることに対応し、規格化の符合が逆になっ
ている。
としたものであることに対応し、規格化の符合が逆になっ
ている。
行列
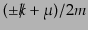 および
および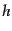 は両方とも2乗すると自分自身に等
しい射影行列である.すると、行列
は両方とも2乗すると自分自身に等
しい射影行列である.すると、行列
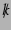 と
と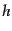 の同時固有ベクトルが
の同時固有ベクトルが
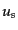 ,
, 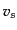 であるから、これら4つの固有ベクトルへの射影行列、すなわち
カシミール演算子の構成により、
であるから、これら4つの固有ベクトルへの射影行列、すなわち
カシミール演算子の構成により、
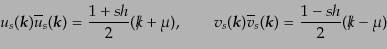 |
(H.4.166) |
という有用な公式が成り立つ。ここで、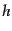 は固有値
は固有値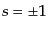 を持つようなス
ピン自由度を分解する射影行列で、ヘリシティをとるときには式
(8.4.163)であるが、他の射影行列でもよい。上の式のスピン和を取っ
たものも有用である:
を持つようなス
ピン自由度を分解する射影行列で、ヘリシティをとるときには式
(8.4.163)であるが、他の射影行列でもよい。上の式のスピン和を取っ
たものも有用である:
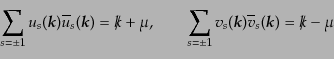 |
(H.4.167) |
こうしてできた解の完全系により、ディラック方程式を満たす場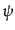 は、
は、
![$\displaystyle \psi(x) = \int \frac{d^3k}{(2\pi)^3 2k^0} \sum_{s=\pm 1} \left[ c...
...ikx} + d_s^*({\mbox{\boldmath$k$}}) v_s({\mbox{\boldmath$k$}}) e^{-ikx} \right]$](img1735.png) |
(H.4.168) |
と展開できる。この形から式(8.4.135)の荷電共役
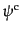 をつ
くるとき、係数
をつ
くるとき、係数 と
と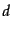 を入れ換えた形
を入れ換えた形
![$\displaystyle \psi^{\rm c} = -i \gamma_2 \psi^* = \int \frac{d^3k}{(2\pi)^3 2k^...
...ikx} + c_s^*({\mbox{\boldmath$k$}}) v_s({\mbox{\boldmath$k$}}) e^{-ikx} \right]$](img1737.png) |
(H.4.169) |
となるためには
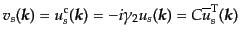 |
(H.4.170) |
であればよいが、この選択は規格化条件(8.4.165)を保っている。
次に、ベクトル場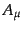 を考える。最もよく知られたベクトル場の例は電磁
場において共変形式でかかれた4元ベクトルポテンシャルのつくる場である。
ベクトルポテンシャルには物理的自由度の他にゲージ自由度が含まれているこ
とがよく知られている。実は、場の量子論においてベクトル場は物理系がゲー
ジ変換という対称性を持つために必要不可欠な場としてのみ現れる。
を考える。最もよく知られたベクトル場の例は電磁
場において共変形式でかかれた4元ベクトルポテンシャルのつくる場である。
ベクトルポテンシャルには物理的自由度の他にゲージ自由度が含まれているこ
とがよく知られている。実は、場の量子論においてベクトル場は物理系がゲー
ジ変換という対称性を持つために必要不可欠な場としてのみ現れる。
そこでまず、電磁場を例に取ってゲージ変換に付随する場としてのベクトル場
を説明しよう。電磁場の共変形式を構成するには,ローレンツ・ヘビサイド単
位系を用いると便利である
H3.この単位系で,マックスウェル
方程式は
| |
|
 |
(H.4.171) |
| |
|
 |
(H.4.172) |
| |
|
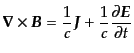 |
(H.4.173) |
| |
|
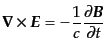 |
(H.4.174) |
と書き表され,ガウス単位系のように が出てくることもなく,また,SI
単位系のように電場
が出てくることもなく,また,SI
単位系のように電場
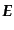 と磁場
と磁場
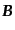 の次元が異なることもない.電
場と磁場はスカラーポテンシャル
の次元が異なることもない.電
場と磁場はスカラーポテンシャル
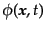 とベクトルポテンシャル
とベクトルポテンシャル
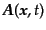 により
により
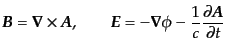 |
(H.4.175) |
により与えられる.電磁場の共変的形式においては,4元ベクトルポテンシャ
ル
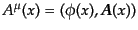 が場の基本的自由度である。マック
スウェル方程式はこの4元ベクトルポテンシャルを用いて一つの運動方程式
が場の基本的自由度である。マック
スウェル方程式はこの4元ベクトルポテンシャルを用いて一つの運動方程式
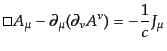 |
(H.4.176) |
にまとめられる。ここで、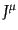 は電荷密度
は電荷密度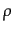 と3次元電流密度
と3次元電流密度
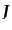 からつくられる4元電流密度
からつくられる4元電流密度
 で
あり、保存則
で
あり、保存則
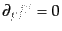 を満たす。この運動方程式は反対称テン
ソル
を満たす。この運動方程式は反対称テン
ソル
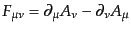 |
(H.4.177) |
を使うと、
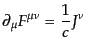 |
(H.4.178) |
という形にも書ける。4元電流密度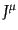 が場
が場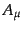 に陽に依存しない場合、
ラグランジアンは
に陽に依存しない場合、
ラグランジアンは
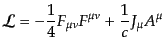 |
(H.4.179) |
となる。真空中 では、電磁場を表すラグランジアンは場の2次の項
のみであり、自由場になる。反対称テンソル
では、電磁場を表すラグランジアンは場の2次の項
のみであり、自由場になる。反対称テンソル
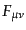 は任意の空間の関数
は任意の空間の関数
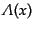 によるベクトルポテンシャルのゲージ変換 (gauge
transformation)
によるベクトルポテンシャルのゲージ変換 (gauge
transformation)
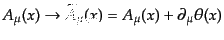 |
(H.4.180) |
において不変である。したがって、ラグランジアンの自由部分もゲージ不変で
あり、真空中の電磁場はゲージ不変であることがわかる。この任意のスカラー
関数を使えば、ベクトルポテンシャルの発散
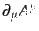 はどのよう
な値にもできる。つまり、ベクトル場の実際の自由度は一つ少なく、4成分の
うち1つは非物理的なゲージ自由度に対応しているのである。
はどのよう
な値にもできる。つまり、ベクトル場の実際の自由度は一つ少なく、4成分の
うち1つは非物理的なゲージ自由度に対応しているのである。
さて、4元電流密度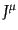 は保存カレントであるから、これはネーターの定理
によると作用の対称性から導かれると考えられる。電流は荷電を持つ物質によ
り担われているものであるから、そのためには、電磁場以外の物質に対しても
ゲージ変換が定義されている必要がある。ここまでに見てきたように、複素ス
カラー場
は保存カレントであるから、これはネーターの定理
によると作用の対称性から導かれると考えられる。電流は荷電を持つ物質によ
り担われているものであるから、そのためには、電磁場以外の物質に対しても
ゲージ変換が定義されている必要がある。ここまでに見てきたように、複素ス
カラー場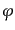 とディラック場
とディラック場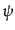 については自由場の場合、全位相変
換について不変であった。このように比較的一般性の高い不変性が電磁場のゲー
ジ変換と何らかの関係にありそうだと思われるであろう。だが、電磁場のゲー
ジ変換は時空間の関数である
については自由場の場合、全位相変
換について不変であった。このように比較的一般性の高い不変性が電磁場のゲー
ジ変換と何らかの関係にありそうだと思われるであろう。だが、電磁場のゲー
ジ変換は時空間の関数である をパラメータとするのに対して、
全位相変換は時空間中で一定の位相
をパラメータとするのに対して、
全位相変換は時空間中で一定の位相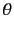 をパラメータとしているので、両
者を同定することはできない。そこで、位相パラメータを時空の関数
をパラメータとしているので、両
者を同定することはできない。そこで、位相パラメータを時空の関数
 として、ある(多成分の)物質場
として、ある(多成分の)物質場 に対して
に対して
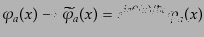 |
|
|
(H.4.181) |
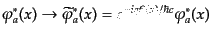 |
|
|
(H.4.182) |
という局所的な全位相変換を考えることにしよう。ここで、指数の中の
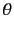 の係数
の係数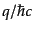 は任意であるが,すぐ下で意味が明らかになる.
位相変換が場所の関数となると、この変換は場の微分と可換でなくなり、式
(8.4.117), (8.4.156)で表される自由場の作用は当然ながら不
変ではなくなる。そこで場の微分の変換をみると、
は任意であるが,すぐ下で意味が明らかになる.
位相変換が場所の関数となると、この変換は場の微分と可換でなくなり、式
(8.4.117), (8.4.156)で表される自由場の作用は当然ながら不
変ではなくなる。そこで場の微分の変換をみると、
![$\displaystyle \partial_\mu \varphi_a \rightarrow \partial_\mu \widetilde{\varph...
...\frac{iq}{\hbar c}[\partial_\mu \theta(x)] e^{iq\theta(x)/\hbar c} \varphi_a(x)$](img1769.png) |
(H.4.183) |
となり、右辺の最後のおつりの項さえなければ、作用は不変に保たれることが
わかる。
そこで、このおつりの項をキャンセルするため、ベクトル場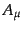 を物質場
を物質場
 と結合させた項を付け加え、物質場の微分を次の共変微分
(covariant derivative)
と結合させた項を付け加え、物質場の微分を次の共変微分
(covariant derivative)
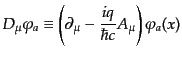 |
(H.4.184) |
で置き換える。電磁場のゲージ変換(8.4.180) により、この共変微分
は位相変換と可換となり、
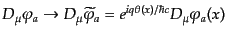 |
(H.4.185) |
と変換することがわかる。こうして、時空間について一定の全位相変換につい
てのみ不変であったもともとの物質場の作用において、場の微分
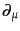 を共変微分
を共変微分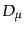 で置き換えれば、局所位相変換についても
不変になる。
で置き換えれば、局所位相変換についても
不変になる。
この共変微分へのおきかえは,電磁スカラーポテンシャル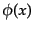 と電磁ベ
クトルポテンシャル
と電磁ベ
クトルポテンシャル
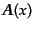 を持つ電磁場中で,電荷
を持つ電磁場中で,電荷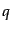 を持つ粒子の非
相対論的シュレーディンガー方程式が
を持つ粒子の非
相対論的シュレーディンガー方程式が
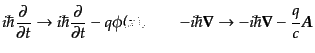 |
(H.4.186) |
の置き換えで得られることに符合している.ここで
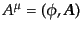 であるから,上のゲージ変換(8.4.181),(8.4.181)
で導入した係数
であるから,上のゲージ変換(8.4.181),(8.4.181)
で導入した係数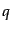 はこの系の表す粒子の電荷を表している.
はこの系の表す粒子の電荷を表している.
こうして、電磁場のゲージ変換と物質場の位相変換が結び付いて
いることがわかる。逆に、電磁場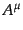 は物質場を局所位相変換について不
変にするためにはなくてはならないものと考えることができる。つまり、まず
対称性ありき、として次にそれを実現させるために必要な場が導入されている、
と考えるのである。このような立場をゲージ原理 (gauge principle)と
いう。こうして導入されるゲージ変換について不変なベクトル場をゲー
ジ場 (gauge field)という。実は、場の理論において、ベクトル場について
は、このようなゲージ場として入される場合以外には、理論が無矛盾になるた
めに不可欠な条件であるくりこみ可能性を満たせないことが知られている。
は物質場を局所位相変換について不
変にするためにはなくてはならないものと考えることができる。つまり、まず
対称性ありき、として次にそれを実現させるために必要な場が導入されている、
と考えるのである。このような立場をゲージ原理 (gauge principle)と
いう。こうして導入されるゲージ変換について不変なベクトル場をゲー
ジ場 (gauge field)という。実は、場の理論において、ベクトル場について
は、このようなゲージ場として入される場合以外には、理論が無矛盾になるた
めに不可欠な条件であるくりこみ可能性を満たせないことが知られている。
こうして、結局ゲージ不変なラグランジアンとしては、複素スカラー場とゲー
ジ場の共存する系について、
![$\displaystyle {\cal L} = - \left[\left(\partial_\mu + \frac{iq}{\hbar c}A_\mu\r...
...u\right)\varphi\right] - \mu^2 \varphi^* \varphi -\frac14 F_{\mu\nu} F^{\mu\nu}$](img1777.png) |
(H.4.187) |
である。このラグランジアンのゲージ不変性によるネーターカレントは
![$\displaystyle j^\mu = \frac{iq}{\hbar c} \left[ \varphi^* (\partial^\mu \varphi...
...mu \varphi^*)\varphi \right] - \frac{2q^2}{\hbar^2 c^2} A^\mu \varphi^* \varphi$](img1778.png) |
(H.4.188) |
である。ラグランジアン(8.4.187)から求められる運動方程式はこの
ネーターカレント(の定数倍)によって式(8.4.177) となるので、まさ
にこのネーターカレントが4元電流密度であることがわかる。同様に、ディラッ
ク場とゲージ場の共存する系のラグランジアンは、
![$\displaystyle {\cal L} = - \overline{\psi} \left[ \gamma^\mu\left(i\partial_\mu...
...rac{q}{\hbar c} A_\mu\right) + mc^2 \right] \psi -\frac14 F_{\mu\nu} F^{\mu\nu}$](img1779.png) |
(H.4.189) |
となり、そのネーターカレントは、
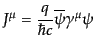 |
(H.4.190) |
となり、これはまさに4元電流密度であることが確かめられる。
ここで、ゲージ場の質量項として
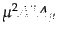 の形の項を考えると、
このような項はゲージ不変性を破ることに注意しよう。すなわち、ゲージ不変
性を満たそうとすると、ゲージ場は質量ゼロでなければならないことになる。
これは光子が質量ゼロであることにまさに符合しているのである。
の形の項を考えると、
このような項はゲージ不変性を破ることに注意しよう。すなわち、ゲージ不変
性を満たそうとすると、ゲージ場は質量ゼロでなければならないことになる。
これは光子が質量ゼロであることにまさに符合しているのである。
このように系のゲージ対称性は、物質と電磁場の結合を規定し、光子の質量が
ゼロであることを自然に説明し、また保存する電荷という概念を導くような、
深い意味を持っているのである。自然界に知られている相互作用はすべてこの
ようなゲージ原理によって理解できることが明らかになっていて、自然界の美
しい真理の一端を垣間見せていると考えられている。電磁場の場合には物質場
のゲージ変換(8.4.181), (8.4.182)は1次元ユニタリ変換で
あるから、群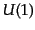 をなしている。この群は可換群であるから、そこから導か
れるゲージ場は可換ゲージ場 (Abelian gauge field)と呼ばれる。これ
に対して、ゲージ変換が非可換群になる場合もあり、そのようなゲージ場は
非可換ゲージ場 (non-Abelian gauge field)と呼ばれる。
をなしている。この群は可換群であるから、そこから導か
れるゲージ場は可換ゲージ場 (Abelian gauge field)と呼ばれる。これ
に対して、ゲージ変換が非可換群になる場合もあり、そのようなゲージ場は
非可換ゲージ場 (non-Abelian gauge field)と呼ばれる。
さて、ベクトル場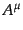 にはゲージ自由度(8.4.180)があるが、この
非物理的な自由度はベクトル場に拘束条件を課すことにより固定することがで
きる。このような拘束条件をゲージ条件 (gauge condition)という。こ
こで、ローレンツゲージ条件
にはゲージ自由度(8.4.180)があるが、この
非物理的な自由度はベクトル場に拘束条件を課すことにより固定することがで
きる。このような拘束条件をゲージ条件 (gauge condition)という。こ
こで、ローレンツゲージ条件
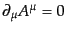 を採用すると、
運動方程式(8.4.176)は特に簡単な形となる。自由場
を採用すると、
運動方程式(8.4.176)は特に簡単な形となる。自由場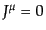 の場
合
の場
合
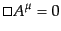 |
(H.4.191) |
となる。この他にもクーロンゲージ
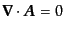 や時間的
ゲージ
や時間的
ゲージ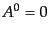 、軸性ゲージ
、軸性ゲージ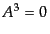 などゲージ条件はいくつも考えられるが、
ローレンツゲージはゲージ固定したあとにもローレンツ共変性があらわに保た
れるという好ましい性質がある。ローレンツゲージの運動方程式では各成分が
質量なしのクラインゴルドン方程式に従っている。したがって、上で調べたス
カラー場やスピノル場の場合と同様にして、平面波展開によって解の完全系を
求められる:
などゲージ条件はいくつも考えられるが、
ローレンツゲージはゲージ固定したあとにもローレンツ共変性があらわに保た
れるという好ましい性質がある。ローレンツゲージの運動方程式では各成分が
質量なしのクラインゴルドン方程式に従っている。したがって、上で調べたス
カラー場やスピノル場の場合と同様にして、平面波展開によって解の完全系を
求められる:
![$\displaystyle A^\mu = \int \frac{d^3k}{(2\pi)^3 2k^0} \sum_{\lambda=0}^3 \left[...
...dmath$k$}}){\varepsilon_\lambda}^{\mu*}({\mbox{\boldmath$k$}}) e^{-ikx} \right]$](img1788.png) |
(H.4.192) |
光子の場合は質量ゼロなので、
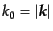 である。また、実ベクトル
場であることを考慮してある。また、
である。また、実ベクトル
場であることを考慮してある。また、
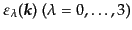 はスピノル場のときの
はスピノル場のときの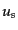 ,
, 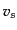 に対応するもので、
偏極ベクトル (polarization vector)と呼ばれる実の量である。偏極ベ
クトルは波数ベクトル
に対応するもので、
偏極ベクトル (polarization vector)と呼ばれる実の量である。偏極ベ
クトルは波数ベクトル
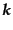 のモードの4つの線形独立な偏極状態を指定
するものであり、お互いに直交する単位ベクトルであればなんでもよい。つま
り、次の直交規格化および完全性の関係を満たすものである:
のモードの4つの線形独立な偏極状態を指定
するものであり、お互いに直交する単位ベクトルであればなんでもよい。つま
り、次の直交規格化および完全性の関係を満たすものである:
| |
|
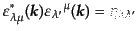 |
(H.4.193) |
| |
|
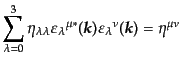 |
(H.4.194) |
ここで、
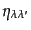 は添字
は添字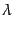 などについてのテンソ
ルであるというわけではなく、単に
などについてのテンソ
ルであるというわけではなく、単に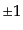 を表す記号として用いているだけ
である。多くの計算では上の直交規格化関係と完全性関係しか必要としないが、
意味をとらえるためにもひとつの具体的な構成を示しておこう。ある座標系を
選んで固定し、はじめの偏極ベクトルとして空間に垂直な単位ベクトル
を表す記号として用いているだけ
である。多くの計算では上の直交規格化関係と完全性関係しか必要としないが、
意味をとらえるためにもひとつの具体的な構成を示しておこう。ある座標系を
選んで固定し、はじめの偏極ベクトルとして空間に垂直な単位ベクトル
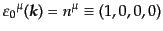 |
(H.4.195) |
を選ぶ。すると残りの3つの偏極ベクトルは空間成分しか持たないので、
 |
(H.4.196) |
の形となる。ここで3次元ベクトル
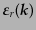 は3次元空
間で規格直交性を満たす:
は3次元空
間で規格直交性を満たす:
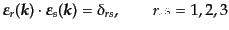 |
(H.4.197) |
さらに
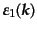 と
と
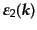 を
を
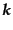 に垂直な面内にとり、
に垂直な面内にとり、
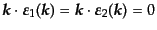 |
(H.4.198) |
とすると、
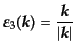 |
(H.4.199) |
となる。こうして構成された偏極ベクトルは
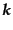 をz軸とするような座標
系では、最も簡単な形
をz軸とするような座標
系では、最も簡単な形
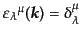 で表され、完全性(8.4.194)を満たしているこ
とは容易にわかる。この偏極ベクトルの構成において
で表され、完全性(8.4.194)を満たしているこ
とは容易にわかる。この偏極ベクトルの構成において
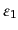 ,
,
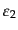 は横偏極 (transverse polarization)、
は横偏極 (transverse polarization)、
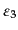 は
縦偏極 (longitudinal polarization)と呼ばれる。さらに
は
縦偏極 (longitudinal polarization)と呼ばれる。さらに
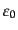 はスカラー偏極 (scalar polarization)、あるいは時間的偏極
(time-like polarization)と呼ばれる。ローレンツゲージ条件を満たすには、
各モードで
はスカラー偏極 (scalar polarization)、あるいは時間的偏極
(time-like polarization)と呼ばれる。ローレンツゲージ条件を満たすには、
各モードで
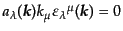 だから、横偏極以外は恒等的にゼロになる。このため、横偏極のみが物理的
成分であり、光子の物理的自由度が2であることに対応している。ただし、ゲー
ジ条件は拘束条件であって、運動方程式(8.4.191)に対する解の完全
系としての展開(8.4.192)には非物理的成分も残してある。縦偏極は
共変的な形で表すと、
だから、横偏極以外は恒等的にゼロになる。このため、横偏極のみが物理的
成分であり、光子の物理的自由度が2であることに対応している。ただし、ゲー
ジ条件は拘束条件であって、運動方程式(8.4.191)に対する解の完全
系としての展開(8.4.192)には非物理的成分も残してある。縦偏極は
共変的な形で表すと、
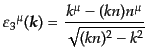 |
(H.4.200) |
となる。ここで実の光子では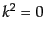 であるが、量子論では
であるが、量子論では
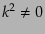 の
場合も必要となるので残してある。ラグランジアンに質量項
の
場合も必要となるので残してある。ラグランジアンに質量項
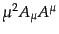 がある場合には縦偏極も物理的成分となるH4。また、線形偏極を
表すときには偏極ベクトルは実数であるが、円偏極や楕円偏極を表すには複素
偏極ベクトルを使う必要があることを注意しておく。また複素ベクトル場の場
合への拡張は、展開(8.4.192)の第2項の
がある場合には縦偏極も物理的成分となるH4。また、線形偏極を
表すときには偏極ベクトルは実数であるが、円偏極や楕円偏極を表すには複素
偏極ベクトルを使う必要があることを注意しておく。また複素ベクトル場の場
合への拡張は、展開(8.4.192)の第2項の
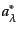 を
を
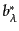 に置き換えればよいことは明らかであろう。
に置き換えればよいことは明らかであろう。
Footnotes
- ...
term)と呼ばれるものであるH2
- 左手系あるいは右手系のみのスピノル
しかない場合には質量が必ずゼロになる、と言われることがあるが、それは誤
りである。
- ...
位系を用いると便利であるH3
- SI単位系(MKSA単位系)に移るには以下で電荷の単位を
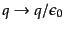 と読みかえ,また
と読みかえ,また
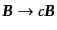 と読みかえる.ローレンツ・ヘビサイド単位系では,微細構造定数
は
と読みかえる.ローレンツ・ヘビサイド単位系では,微細構造定数
は
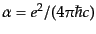 である.
である.
- ...がある場合には縦偏極も物理的成分となるH4
- ゲージ場には質量
項はもともと含まれないが、この場合でも実は、自発的対称性の破れという機
構によって見掛け上の質量項が現れることができる。実際、弱い相互作用にお
いてはこの機構によりゲージ場が質量を獲得している。





次へ: 自由場の量子化
上へ: 場の量子化と粒子の相互作用
前へ: 相対論的に可能な場
目次
索引
All rights reserved © T.Matsubara 2004-2010
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11
![]() を考える。ここで、
を考える。ここで、
![]() は時空座標
は時空座標![]() を省略して表している。実スカラー場の場合,場の時
間微分について2次で、かつ場の1階微分までしか含まないローレンツ不変な
ラグランジアン密度としては,次の形しかないことがわかる:
を省略して表している。実スカラー場の場合,場の時
間微分について2次で、かつ場の1階微分までしか含まないローレンツ不変な
ラグランジアン密度としては,次の形しかないことがわかる:
![]() であれば自由場となる。その場合ラグランジアン密度は、
であれば自由場となる。その場合ラグランジアン密度は、
![]() の対称性を持つ
の対称性を持つ
![]() モデルがある。そのラグランジアン密度は
モデルがある。そのラグランジアン密度は
![]() とおけば、
とおけば、
![]() のラグランジアン密度としては
のラグランジアン密度としては
![]() からスカラー量を作るために、
式(8.3.90)で導入された
からスカラー量を作るために、
式(8.3.90)で導入された
![]() ,
,
![]() を利用すればよい。すると、
を利用すればよい。すると、
![]() スピ
ノル
スピ
ノル
![]() からつくるローレンツ不変な組み合わせとして、
からつくるローレンツ不変な組み合わせとして、
![]() と
いうものが考えられる。この形のままでは実数ではないので複素共役を使って
実数にする。
と
いうものが考えられる。この形のままでは実数ではないので複素共役を使って
実数にする。
![]() は、
は、
![]() は空間反転に対して、
は空間反転に対して、
![]() は空間の添字が一つ
なので符合を変え、
は空間の添字が一つ
なので符合を変え、
![]() は符合を変えない。すると、式
(8.3.64), (8.3.65)より、生成子
は符合を変えない。すると、式
(8.3.64), (8.3.65)より、生成子
![]() と
と
![]() がお互いに入れ替わることになり、
がお互いに入れ替わることになり、![]() 表現は
表現は![]() 表現に
なる。これは空間反転について、
表現に
なる。これは空間反転について、
![]() 、すなわち、
、すなわち、
![]() と入れ替わることを意味する。2つのスピノルを区別す
るR, Lは、この性質を反映し、
と入れ替わることを意味する。2つのスピノルを区別す
るR, Lは、この性質を反映し、
![]() は右手系のスピノル、
は右手系のスピノル、
![]() は左手系のスピノルと考えることを表しているのである。どち
らかが左または右である必然性はなく、単に便宜的に決っているだけである。
は左手系のスピノルと考えることを表しているのである。どち
らかが左または右である必然性はなく、単に便宜的に決っているだけである。
![]() スピノルの複素共役は
スピノルの複素共役は
![]() スピノルとなり、逆に
スピノルとなり、逆に
![]() スピノルの複素共役は
スピノルの複素共役は
![]() スピノルとなるので、ディラック
スピノル(8.4.128)からつくる
スピノルとなるので、ディラック
スピノル(8.4.128)からつくる
![]() である。もし、スピノ
ルがグラスマン数でなければ
である。もし、スピノ
ルがグラスマン数でなければ
![]() が反対称だからこの組み合わせは
ゼロになってしまうが、グラスマン数ゆえに、このような項が生き残れるので
ある。このことに注意して、複素共役との足し合わせにより実数をつくればそ
れが質量項となる。左手系も同様にして、
が反対称だからこの組み合わせは
ゼロになってしまうが、グラスマン数ゆえに、このような項が生き残れるので
ある。このことに注意して、複素共役との足し合わせにより実数をつくればそ
れが質量項となる。左手系も同様にして、
![]() を満たす4元ベクトル
を満たす4元ベクトル
![]() と4成分スピノル
と4成分スピノル
![]() により、
により、
![]() という形を基本モードとしてもつことがわかる。ここで、
という形を基本モードとしてもつことがわかる。ここで、
![]() はそれぞれのモードについて
はそれぞれのモードについて
![]() および
および![]() は両方とも2乗すると自分自身に等
しい射影行列である.すると、行列
は両方とも2乗すると自分自身に等
しい射影行列である.すると、行列
![]() と
と![]() の同時固有ベクトルが
の同時固有ベクトルが
![]() ,
, ![]() であるから、これら4つの固有ベクトルへの射影行列、すなわち
カシミール演算子の構成により、
であるから、これら4つの固有ベクトルへの射影行列、すなわち
カシミール演算子の構成により、
![]() は、
は、
![]() を考える。最もよく知られたベクトル場の例は電磁
場において共変形式でかかれた4元ベクトルポテンシャルのつくる場である。
ベクトルポテンシャルには物理的自由度の他にゲージ自由度が含まれているこ
とがよく知られている。実は、場の量子論においてベクトル場は物理系がゲー
ジ変換という対称性を持つために必要不可欠な場としてのみ現れる。
を考える。最もよく知られたベクトル場の例は電磁
場において共変形式でかかれた4元ベクトルポテンシャルのつくる場である。
ベクトルポテンシャルには物理的自由度の他にゲージ自由度が含まれているこ
とがよく知られている。実は、場の量子論においてベクトル場は物理系がゲー
ジ変換という対称性を持つために必要不可欠な場としてのみ現れる。
![]() は保存カレントであるから、これはネーターの定理
によると作用の対称性から導かれると考えられる。電流は荷電を持つ物質によ
り担われているものであるから、そのためには、電磁場以外の物質に対しても
ゲージ変換が定義されている必要がある。ここまでに見てきたように、複素ス
カラー場
は保存カレントであるから、これはネーターの定理
によると作用の対称性から導かれると考えられる。電流は荷電を持つ物質によ
り担われているものであるから、そのためには、電磁場以外の物質に対しても
ゲージ変換が定義されている必要がある。ここまでに見てきたように、複素ス
カラー場![]() とディラック場
とディラック場![]() については自由場の場合、全位相変
換について不変であった。このように比較的一般性の高い不変性が電磁場のゲー
ジ変換と何らかの関係にありそうだと思われるであろう。だが、電磁場のゲー
ジ変換は時空間の関数である
については自由場の場合、全位相変
換について不変であった。このように比較的一般性の高い不変性が電磁場のゲー
ジ変換と何らかの関係にありそうだと思われるであろう。だが、電磁場のゲー
ジ変換は時空間の関数である![]() をパラメータとするのに対して、
全位相変換は時空間中で一定の位相
をパラメータとするのに対して、
全位相変換は時空間中で一定の位相![]() をパラメータとしているので、両
者を同定することはできない。そこで、位相パラメータを時空の関数
をパラメータとしているので、両
者を同定することはできない。そこで、位相パラメータを時空の関数
![]() として、ある(多成分の)物質場
として、ある(多成分の)物質場![]() に対して
に対して
![]() を物質場
を物質場
![]() と結合させた項を付け加え、物質場の微分を次の共変微分
(covariant derivative)
と結合させた項を付け加え、物質場の微分を次の共変微分
(covariant derivative)
![]() と電磁ベ
クトルポテンシャル
と電磁ベ
クトルポテンシャル
![]() を持つ電磁場中で,電荷
を持つ電磁場中で,電荷![]() を持つ粒子の非
相対論的シュレーディンガー方程式が
を持つ粒子の非
相対論的シュレーディンガー方程式が
![]() は物質場を局所位相変換について不
変にするためにはなくてはならないものと考えることができる。つまり、まず
対称性ありき、として次にそれを実現させるために必要な場が導入されている、
と考えるのである。このような立場をゲージ原理 (gauge principle)と
いう。こうして導入されるゲージ変換について不変なベクトル場をゲー
ジ場 (gauge field)という。実は、場の理論において、ベクトル場について
は、このようなゲージ場として入される場合以外には、理論が無矛盾になるた
めに不可欠な条件であるくりこみ可能性を満たせないことが知られている。
は物質場を局所位相変換について不
変にするためにはなくてはならないものと考えることができる。つまり、まず
対称性ありき、として次にそれを実現させるために必要な場が導入されている、
と考えるのである。このような立場をゲージ原理 (gauge principle)と
いう。こうして導入されるゲージ変換について不変なベクトル場をゲー
ジ場 (gauge field)という。実は、場の理論において、ベクトル場について
は、このようなゲージ場として入される場合以外には、理論が無矛盾になるた
めに不可欠な条件であるくりこみ可能性を満たせないことが知られている。
![]() の形の項を考えると、
このような項はゲージ不変性を破ることに注意しよう。すなわち、ゲージ不変
性を満たそうとすると、ゲージ場は質量ゼロでなければならないことになる。
これは光子が質量ゼロであることにまさに符合しているのである。
の形の項を考えると、
このような項はゲージ不変性を破ることに注意しよう。すなわち、ゲージ不変
性を満たそうとすると、ゲージ場は質量ゼロでなければならないことになる。
これは光子が質量ゼロであることにまさに符合しているのである。
![]() をなしている。この群は可換群であるから、そこから導か
れるゲージ場は可換ゲージ場 (Abelian gauge field)と呼ばれる。これ
に対して、ゲージ変換が非可換群になる場合もあり、そのようなゲージ場は
非可換ゲージ場 (non-Abelian gauge field)と呼ばれる。
をなしている。この群は可換群であるから、そこから導か
れるゲージ場は可換ゲージ場 (Abelian gauge field)と呼ばれる。これ
に対して、ゲージ変換が非可換群になる場合もあり、そのようなゲージ場は
非可換ゲージ場 (non-Abelian gauge field)と呼ばれる。
![]() にはゲージ自由度(8.4.180)があるが、この
非物理的な自由度はベクトル場に拘束条件を課すことにより固定することがで
きる。このような拘束条件をゲージ条件 (gauge condition)という。こ
こで、ローレンツゲージ条件
にはゲージ自由度(8.4.180)があるが、この
非物理的な自由度はベクトル場に拘束条件を課すことにより固定することがで
きる。このような拘束条件をゲージ条件 (gauge condition)という。こ
こで、ローレンツゲージ条件
![]() を採用すると、
運動方程式(8.4.176)は特に簡単な形となる。自由場
を採用すると、
運動方程式(8.4.176)は特に簡単な形となる。自由場![]() の場
合
の場
合
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11