




次へ: 膨張宇宙における光子と電子の相互作用
上へ: 相対論的運動学
前へ: 相対論的分布関数と巨視的変数
目次
索引
Subsections
分布関数は粒子の統計的性質を表す基本的な関数であるが,非平衡系では分布
関数はボルツマン方程式を解くことによって求められる.この節では,一般相
対論的なボルツマン方程式を導出する.
粒子が重力のみの影響を受けて運動する場合,その軌跡は測地線の方程式
(B.2.56)に従う:
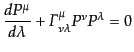 |
(I.2.18) |
ここで,
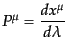 |
(I.2.19) |
は4元運動量である.また,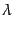 はアフィンパラメータであるが,粒子に
質量がある場合は粒子に沿った固有時間を質量で割ったものとなる.いま,電
磁場など他の力は粒子に働いていないものとする.
はアフィンパラメータであるが,粒子に
質量がある場合は粒子に沿った固有時間を質量で割ったものとなる.いま,電
磁場など他の力は粒子に働いていないものとする.
このとき,8次元位相空間の不変体積要素
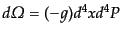 |
(I.2.20) |
が粒子の測地線に沿って不変となることを示そう.式(9.2.18),
(9.2.19)により,アフィンパラメータ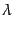 が
が
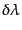 だ
け変化するとき,粒子の位相空間中での座標は
だ
け変化するとき,粒子の位相空間中での座標は
と変化する.すると,不変体積要素
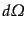 の変化は
の変化は
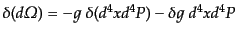 |
(I.2.23) |
となる.ここで,体積要素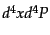 の変化はヤコビアン
の変化はヤコビアン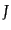 がわかれば計算
されるが,それは
がわかれば計算
されるが,それは
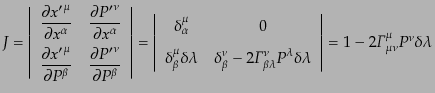 |
(I.2.24) |
となる.ここで,接続を計量で表し,さらに,行列式の微分の
式(B.2.42)を用いると,
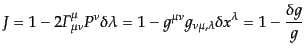 |
(I.2.25) |
であることがわかる.したがって,結局式(9.2.23)は
![$\displaystyle \delta(d{\mit\Omega}) = -g \left[(J - 1) + \frac{\delta g}{g}\right]d^4xd^4P = 0$](img2527.png) |
(I.2.26) |
となる.これにより,8次元位相空間の不変体積要素は粒子の測地線に沿って
不変となることが証明された.
さて,位置についての不変体積
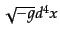 は,ある座標系における空間
方向の3次元不変体積
は,ある座標系における空間
方向の3次元不変体積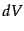 と,これに垂直な方向を向いた長さ
と,これに垂直な方向を向いた長さ の時間的間
隔分との積
の時間的間
隔分との積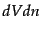 で与えられる.いま,ベクトル
で与えられる.いま,ベクトル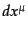 を、粒子の世界線が
この微小体積中と交わる長さと同じ長さを持ち,粒子の世界線に沿った方向を
持つようなものとする.すると,長さ
を、粒子の世界線が
この微小体積中と交わる長さと同じ長さを持ち,粒子の世界線に沿った方向を
持つようなものとする.すると,長さ はこのベクトルの
はこのベクトルの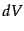 に垂直な方向
の成分となる.そこで,
に垂直な方向
の成分となる.そこで,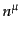 を
を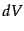 に垂直な,時間的単位ベクトルとし,
また微小体積中での粒子のアフィンパラメータの幅を
に垂直な,時間的単位ベクトルとし,
また微小体積中での粒子のアフィンパラメータの幅を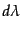 とすると,
とすると,
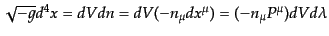 |
(I.2.27) |
と表されることになる.この式に
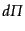 をかけることにより,
をかけることにより,
 |
(I.2.28) |
となる.ここで,右辺は粒子に沿って一定である.事実,不変体積素片
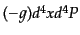 が一定であることは上で証明した.また,粒子のエネルギーの
符合が変化することはない.また,運動に際して
が一定であることは上で証明した.また,粒子のエネルギーの
符合が変化することはない.また,運動に際して
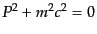 は常に
成り立っているので、
は常に
成り立っているので、
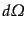 の中で粒子はこの関係を満たす断面にのみ存
在する.したがってその断面の体積は不変になる.また,
の中で粒子はこの関係を満たす断面にのみ存
在する.したがってその断面の体積は不変になる.また,
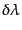 と
と
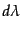 は独立であるから
は独立であるから
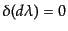 ,すなわち
,すなわち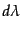 は
運動に沿って一定である.したがって,粒子の運動に沿って取った次の量は一
定であることが証明されたことになる:
は
運動に沿って一定である.したがって,粒子の運動に沿って取った次の量は一
定であることが証明されたことになる:
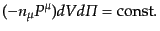 |
(I.2.29) |
このことをリュービルの定理(Liouville theorem)という.
任意の座標系に取られたある時刻の空間の微小体積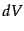 を横切る粒子のうち,
運動量が
を横切る粒子のうち,
運動量が
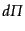 の範囲にあるものの数を
の範囲にあるものの数を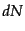 とする.微小体積
とする.微小体積
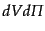 中に
ある粒子4元流束は
中に
ある粒子4元流束は
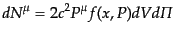 |
(I.2.30) |
となるが,粒子数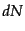 はこの4元流束の
はこの4元流束の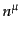 方向の成分により与えられるの
で,
方向の成分により与えられるの
で,
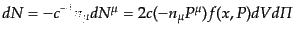 |
(I.2.31) |
であることがわかる.すると,リュービルの定理から粒子の測地線に沿って
の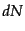 の変化は
の変化は
となる.
粒子に重力以外の相互作用が働かない場合は微小体積
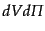 中の粒子の数
は粒子の測地線に沿って一定となる.このときには式(9.2.32)はゼロに
なり,したがって,次の相対論的なリュービル方程式(Liouville
equation)
中の粒子の数
は粒子の測地線に沿って一定となる.このときには式(9.2.32)はゼロに
なり,したがって,次の相対論的なリュービル方程式(Liouville
equation)
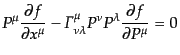 |
(I.2.33) |
が成り立つ.この方程式はブラソフ方程式(Vlasov equation)あるいは
無衝突ボルツマン方程式(Collisionless Boltzmann equation)とも呼ば
れる.ただしいま分布関数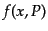 にはすでに
にはすでに
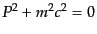 を
を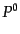 に
ついて解いた関係
に
ついて解いた関係
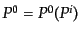 が代入されて
が代入されて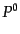 には陽に依存しないも
のと考えれば,上の式で
には陽に依存しないも
のと考えれば,上の式で
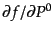 はゼロである.左辺の
はゼロである.左辺の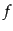 に作用する演算子
に作用する演算子
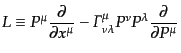 |
(I.2.34) |
をリュービル演算子(Liouville operator)と呼ぶ.この記法でリュービ
ル方程式は![$ L[f] = 0$](img2552.png) と表される.
と表される.
粒子に重力以外の相互作用がある場合は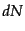 が消えず,位相空間素片中で粒子
が出入りすることになる.粒子の運動に沿ってアフィンパラメータが
が消えず,位相空間素片中で粒子
が出入りすることになる.粒子の運動に沿ってアフィンパラメータが
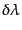 だけ変化する間の,
だけ変化する間の,
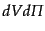 中の粒子数が変化を
中の粒子数が変化を
![$\displaystyle dN = C[f]\cdot 2c\;(- n_\mu P^\mu) dV d{\mit\Pi}\delta\lambda$](img2553.png) |
(I.2.35) |
とおく.この場合には,次の相対論的なボルツマン方程式(Boltzmann
equation)が得られる:
![$\displaystyle P^\mu \frac{\partial f}{\partial x^\mu} - {\mit\Gamma}^\mu_{\nu\lambda} P^\nu P^\lambda \frac{\partial f}{\partial P^\mu} = C[f]$](img2554.png) |
(I.2.36) |
ここで,![$ C[f]$](img2555.png) は衝突項と呼ばれ,粒子の相互作用の詳細から決まる.リュー
ビル演算子を用いて簡略化すれば
は衝突項と呼ばれ,粒子の相互作用の詳細から決まる.リュー
ビル演算子を用いて簡略化すれば
![$ L[f] = C[f]$](img2556.png) と表される.
と表される.
ここで、式(9.1.6)で与えられる粒子4元速度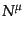 ,また式
(9.1.14)で与えられるエネルギー運動量テンソル
,また式
(9.1.14)で与えられるエネルギー運動量テンソル
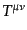 の発散に
関して,次の式が成り立つ.
の発散に
関して,次の式が成り立つ.
| |
|
![$\displaystyle {N^\mu}_{;\mu} = 2c^2 \int d{\mit\Pi}L[f] = 2c^2 \int d{\mit\Pi}C[f]$](img2558.png) |
(I.2.37) |
| |
|
![$\displaystyle {T^{\mu\nu}}_{;\nu} =
2c^2 \int d{\mit\Pi}P^\mu L[f] = 2c^2 \int d{\mit\Pi}P^\mu C[f]$](img2559.png) |
(I.2.38) |
これらの式の後半部分はボルツマン方程式から明らかである.前半部分もあら
わに計算することによって示される.まず,式
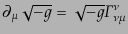 |
(I.2.39) |
を用いて最初の式を微分することにより,
| |
|
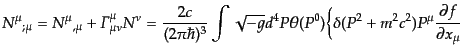 |
|
| |
|
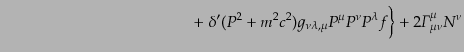 |
(I.2.40) |
となる.ここでリュービル演算子の定義式(9.2.34)を代入してさらに
部分積分すると,
となる.ここで,エネルギーは正であるから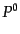 の符号は変化しないこと,
およびクリストッフェル記号の定義式から容易に示せる次の式
の符号は変化しないこと,
およびクリストッフェル記号の定義式から容易に示せる次の式
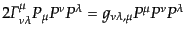 |
(I.2.42) |
を用いた.式(9.2.41)を式(9.2.40)へ代入すれば式
(9.2.37)が示される.式(9.2.38)も同様の計算により示さ
れる.
次に,ボルツマン方程式の衝突項を考える.ボルツマン方程式の左辺は重力場
中で粒子が自由運動する場合の位相空間の密度の時間変化分を記述するもので,
衝突項は粒子同士の相互作用により粒子が位相空間の別の部分へ移動する変化
分を表す.衝突の過程を詳しく記述するのは困難であるが,現実には粒子同士
の相互作用は非常に短い距離で,かつ短い時間に起こっている.そのため,次
の仮定をしてもよいと考えられるる:
- 長距離力としては重力のみが寄与する.
- 短距離力は粒子同士の衝突や生成消滅過程として瞬間的に作用するもの
と近似できる.
強い相互作用や弱い相互作用は極めて短距離にしか効かないので,衝突過程に
おいてこの近似は極めてよい.電磁力はなにも遮蔽するものがなければ長距離
力になり得るが,現実的には宇宙は全体として中性であるから長距離ではまわ
りの電荷に遮蔽されて実質的には短距離力になる.唯一重力は遮蔽手段が存在
しないので,かならず長距離力として作用する.現実の実験などでは重力の効
果は非常に弱く,これも無視して取り扱ってかまわないが,宇宙の中での大規
模な運動を考えるときには重力は無視できなくなってくるので,含めておく必
要がある.この仮定のもと,衝突項を具体的に粒子間の相互作用によって表す
ことを考える.
前章で詳しくみたように,粒子の反応は場の量子論によって最も正確に記述さ
れる.粒子の種類はローレンツ群の表現の種類で分類され,各々の自由度は異
なるが,まとめてコンパクトな記号で表しておくと便利である.いま相互作用
に関係する粒子種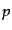 の生成消滅演算子を
の生成消滅演算子を
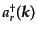 ,
,
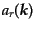 と書くことにする.ここで,添字の
と書くことにする.ここで,添字の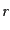 はこの粒子の種類とさ
らに内部自由度の違いも区別するものとする.例えば,スカラー粒子,スピン
はこの粒子の種類とさ
らに内部自由度の違いも区別するものとする.例えば,スカラー粒子,スピン
 の電子,スピン
の電子,スピン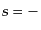 の電子,偏極
の電子,偏極
 の光子,偏極
の光子,偏極
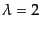 の光子,などはすべて異なる
の光子,などはすべて異なる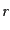 に属する.これらはまとめて,次の(反)
交換関係を満たす:
に属する.これらはまとめて,次の(反)
交換関係を満たす:
| |
|
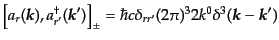 |
(I.2.43) |
| |
|
![$\displaystyle \left[
a_r({\mbox{\boldmath$k$}}), a_{r'}({\mbox{\boldmath$k$}}'...
...mbox{\boldmath$k$}}), a_{r'}^\dagger({\mbox{\boldmath$k$}}')
\right]_{\pm} = 0$](img2575.png) |
(I.2.44) |
ここで,
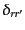 は粒子種と内部自由度がともに等しいときのみ
は粒子種と内部自由度がともに等しいときのみ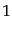 と
なるクロネッカーデルタである.また,フェルミ粒子同士の場合反交換関係
と
なるクロネッカーデルタである.また,フェルミ粒子同士の場合反交換関係
![$ [a,b]_+ = ab + ba$](img2577.png) ,どちらかがボース粒子の場合交換関係
,どちらかがボース粒子の場合交換関係
![$ [a,b]_- = ab -
ba$](img2578.png) を取る.ここで,式(8.5.205)の下で行ったのと同様に,周期境界
条件の有限体積
を取る.ここで,式(8.5.205)の下で行ったのと同様に,周期境界
条件の有限体積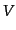 により波数空間を離散化すると,
により波数空間を離散化すると,
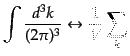 |
|
|
(I.2.45) |
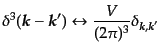 |
|
|
(I.2.46) |
と対応し,離散化された運動量空間での演算子
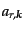 は
は
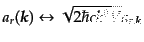 |
(I.2.47) |
と対応し,自由度はすべて有限になる.ここで記法を簡略化して,自由度
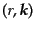 をまとめて添字
をまとめて添字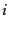 などで表すことにして,その生成消滅演算子
を
などで表すことにして,その生成消滅演算子
を
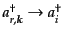 ,
,
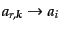 などとする.すなわち,この新たな添字は,粒子種の違い,
内部自由度の違い,および離散化された波数ベクトルの違いをすべて区別する.
この簡略化された記法で交換関係(9.2.43), (9.2.44)はシ
ンプルに
などとする.すなわち,この新たな添字は,粒子種の違い,
内部自由度の違い,および離散化された波数ベクトルの違いをすべて区別する.
この簡略化された記法で交換関係(9.2.43), (9.2.44)はシ
ンプルに
| |
|
![$\displaystyle \left[a_i, a_j^\dagger\right]_{\pm}
= \delta_{ij}$](img2584.png) |
(I.2.48) |
| |
|
![$\displaystyle \left[a_i, a_j\right]_{\pm} =
\left[a_i^\dagger, a_j^\dagger\right]_{\pm}
= 0$](img2585.png) |
(I.2.49) |
と表される.ここで,
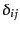 は粒子種,内部自由度,波数ベクトルが
すべて一致したときのみ
は粒子種,内部自由度,波数ベクトルが
すべて一致したときのみ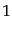 となるクロネッカーデルタである.
となるクロネッカーデルタである.
この記法において,状態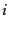 にある粒子が
にある粒子が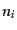 個ずつ存在する状態ベクトルは
個ずつ存在する状態ベクトルは
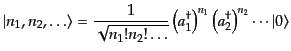 |
(I.2.50) |
となる.ここでこの状態ベクトルは1に規格化されている.このような状態ベ
クトルで,粒子数の合計が有限であるようなもの(
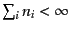 )の
全体はフォック空間の正規直交基底をなすのであった.状態(9.2.50)
に生成演算子,消滅演算子を作用させると,交換関係(9.2.50)からす
ぐわかるように,
)の
全体はフォック空間の正規直交基底をなすのであった.状態(9.2.50)
に生成演算子,消滅演算子を作用させると,交換関係(9.2.50)からす
ぐわかるように,
| |
|
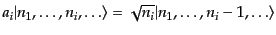 |
(I.2.51) |
| |
|
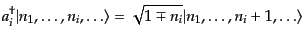 |
(I.2.52) |
となる.ここで,第二式において上の符号はフェルミ粒子の場合,下の符号は
ボース粒子の場合である.以下現れてくる多重符号も同様である.
この準備のもと,時空のある領域Dの中での衝突
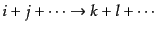 を考える.はじめの仮定に基づき,領域Dは十分小さく、この
中では時空の曲率が無視できて平坦時空の場の量子論が適用できるものとする.
また,同時に衝突の時空間隔よりは十分大きく,漸近場による散乱理論が適用
できるものとする.領域Dの体積を
を考える.はじめの仮定に基づき,領域Dは十分小さく、この
中では時空の曲率が無視できて平坦時空の場の量子論が適用できるものとする.
また,同時に衝突の時空間隔よりは十分大きく,漸近場による散乱理論が適用
できるものとする.領域Dの体積を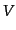 , 時間間隔を
, 時間間隔を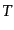 として,この体積を上
で運動量の離散化に用いた体積と同一視する.いま,始状態として多粒子系の
状態ベクトル
として,この体積を上
で運動量の離散化に用いた体積と同一視する.いま,始状態として多粒子系の
状態ベクトル
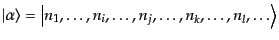 |
(I.2.53) |
をとる.すると衝突後の終状態は
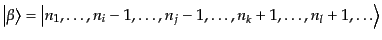 |
(I.2.54) |
と表される.終状態の状態ベクトルは始状態の漸近的自由ハイゼンベルグ場に
より構成されたフォック空間の基底により表されている.これら状態間の遷移
確率はS行列要素
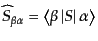 |
(I.2.55) |
の絶対値の2乗
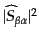 により与えられる.ここで
のS行列要素はS行列演算子を1で規格化された状態ベクトルではさんだもので
あるが,下では不変規格化された状態ベクトルではさんだS行列要素が表れる
ので,区別するためにハットをつけてある.
により与えられる.ここで
のS行列要素はS行列演算子を1で規格化された状態ベクトルではさんだもので
あるが,下では不変規格化された状態ベクトルではさんだS行列要素が表れる
ので,区別するためにハットをつけてある.
ここで,S行列演算子はダイソンの公式により場の演算子の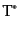 積の和
で与えられ,さらにウィックの定理により正規順序積の和に展開されるから,
一般的に連続表示において
積の和
で与えられ,さらにウィックの定理により正規順序積の和に展開されるから,
一般的に連続表示において
| |
|
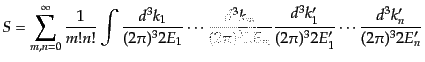 |
|
| |
|
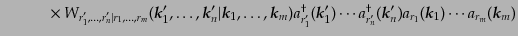 |
(I.2.56) |
という形になる.ここで,
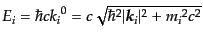 などは相互作用を行っている粒子のエネル
ギーに対応する量であり,積分測度をローレンツ不変にするためにつけてある.
積分カーネルの形
などは相互作用を行っている粒子のエネル
ギーに対応する量であり,積分測度をローレンツ不変にするためにつけてある.
積分カーネルの形
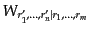 は系の相互作用ラ
グランジアンから一意的にきまるものである.上式の形からS行列要素を作っ
てみると,左右からはさんだ生成消滅演算子がちょうど同じ数だけある項のみ
生き残るので,
は系の相互作用ラ
グランジアンから一意的にきまるものである.上式の形からS行列要素を作っ
てみると,左右からはさんだ生成消滅演算子がちょうど同じ数だけある項のみ
生き残るので,
| |
|
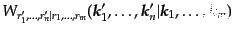 |
|
| |
|
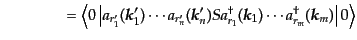 |
(I.2.57) |
となって,この積分カーネルは不変規格化されたS行列要素である.式
(9.2.56)のS行列演算子の形を離散化された波数空間の表示にすると,
式(9.2.45), (9.2.47)の対応より,
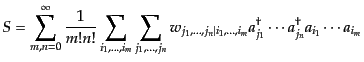 |
(I.2.58) |
の形となる.ここで係数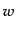 は式(9.2.56)のカーネル
は式(9.2.56)のカーネル と関係する.
その関係は,対応する自由度を
と関係する.
その関係は,対応する自由度を
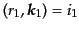 などと対応させれば,
などと対応させれば,
| |
|
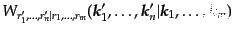 |
|
| |
|
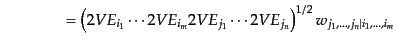 |
(I.2.59) |
である.さらに
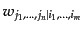 は反
応
は反
応
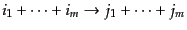 の1に規格化された
S行列要素
の1に規格化された
S行列要素
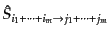 に等しい.
に等しい.
式(9.2.53), (9.2.54), (9.2.58)を式
(9.2.55)に入れることでS行列要素の形が求まる.ここで,摂動の最
低次の近似においては,始状態と終状態の粒子から出てくる生成消滅演算子の
うち,衝突
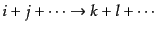 に関係するもののみがS行列
演算子とペアを作る.なぜなら,ある量子状態にある始状態の粒子が,相互作
用の結果として同じ量子状態の終状態として表れるファインマン図は,始状態
がそのまま終状態につながっているようなファインマン図よりも摂動の次数が
高くなるからである.したがって,摂動の最低次の近似では展開
(9.2.58)の一種類の項だけがS行列要素に寄与し,始状態および終状
態の粒子の並び替えの自由度を考慮して
に関係するもののみがS行列
演算子とペアを作る.なぜなら,ある量子状態にある始状態の粒子が,相互作
用の結果として同じ量子状態の終状態として表れるファインマン図は,始状態
がそのまま終状態につながっているようなファインマン図よりも摂動の次数が
高くなるからである.したがって,摂動の最低次の近似では展開
(9.2.58)の一種類の項だけがS行列要素に寄与し,始状態および終状
態の粒子の並び替えの自由度を考慮して
となる.ここで,2番目の等式では式(9.2.51), (9.2.52)
を用いた.また,始状態と終状態の量子状態はお互いにすべて異なっているも
ののみを考えている.もし始状態と終状態に同じものが含まれていれば,それ
は始状態から終状態へ直接つながるファインマン図で表される,より低い摂動
の反応で実現できるため,摂動の最低次においては考える必要はない.このS
行列要素の絶対値2乗により,領域D中で,多粒子系の始状態
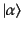 から終状態
から終状態
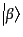 へ,一度の衝突
へ,一度の衝突
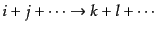 によって遷移するときの遷移確率
によって遷移するときの遷移確率
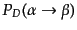 が求められる:
が求められる:
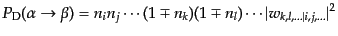 |
(I.2.61) |
この式において,左辺は多粒子系全体の状態間の遷移確率を表しているが,右
辺は反応に関係する量子状態の,始状態における占有数
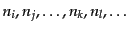 ,およびその反応のS行列要素により決定す
る.したがって反応に関係しない量子状態はこの遷移確率に影響を及ぼさない.
ちなみに,この結論はもちろん摂動の最低次近似をとったからであり,高次効
果を含めると事態はもっと複雑化する.この確率は,反応によって粒子が消滅
する
,およびその反応のS行列要素により決定す
る.したがって反応に関係しない量子状態はこの遷移確率に影響を及ぼさない.
ちなみに,この結論はもちろん摂動の最低次近似をとったからであり,高次効
果を含めると事態はもっと複雑化する.この確率は,反応によって粒子が消滅
する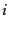 などの量子状態についてはその始状態での数
などの量子状態についてはその始状態での数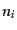 などに比例する.そ
の意味としては,はじめに数が多ければ多いほど反応の確率が増えるからであ
ると解釈できる.一方,反応によって粒子が生成される
などに比例する.そ
の意味としては,はじめに数が多ければ多いほど反応の確率が増えるからであ
ると解釈できる.一方,反応によって粒子が生成される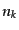 などの量子状態
については,フェルミ粒子の場合
などの量子状態
については,フェルミ粒子の場合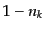 などに比例する.パウリの排他律に
より,フェルミ粒子は同じ量子状態を複数の粒子で占めることはできないので,
このとき
などに比例する.パウリの排他律に
より,フェルミ粒子は同じ量子状態を複数の粒子で占めることはできないので,
このとき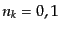 のみしかとり得ない.するとこの因子
のみしかとり得ない.するとこの因子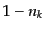 は,すで
に占められている量子状態に対して反応後に粒子が生成される確率がゼロであ
ることを表している.つまりこの因子はパウリの排他律により粒子の生成を阻
害する,ブロッキング因子である.また,反応後の粒子がボース粒子の場合に
は遷移確率は
は,すで
に占められている量子状態に対して反応後に粒子が生成される確率がゼロであ
ることを表している.つまりこの因子はパウリの排他律により粒子の生成を阻
害する,ブロッキング因子である.また,反応後の粒子がボース粒子の場合に
は遷移確率は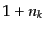 などに比例する.ボース粒子は同じ量子状態を粒子がい
くらでも占めることができるが,はじめに多く占められている量子状態には,
反応によりその量子状態の粒子の生成確率が大きくなることを表している
I1.つまりこの因子はす
でにある量子状態をさらに増やす反応を誘うような,誘導因子である.
などに比例する.ボース粒子は同じ量子状態を粒子がい
くらでも占めることができるが,はじめに多く占められている量子状態には,
反応によりその量子状態の粒子の生成確率が大きくなることを表している
I1.つまりこの因子はす
でにある量子状態をさらに増やす反応を誘うような,誘導因子である.
さて,式(9.2.61)の遷移確率はひとつの始状態
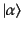 が与え
られたとき,ある終状態
が与え
られたとき,ある終状態
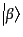 に反応する確率を表している.ここで,
始状態において占められている粒子数
に反応する確率を表している.ここで,
始状態において占められている粒子数
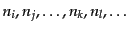 につ
いての統計平均をとれば,この反応が起きる確率を与えることになる.統計平
均をとるときには異なる量子状態間に相関はなく,
につ
いての統計平均をとれば,この反応が起きる確率を与えることになる.統計平
均をとるときには異なる量子状態間に相関はなく,
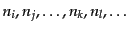 は各量子状態の粒子数の平均値
は各量子状態の粒子数の平均値
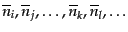 に置き換えられることになる.平均値
に置き換えられることになる.平均値
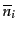 は領域Dにおける粒子
は領域Dにおける粒子
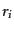 の運動量分布関数
の運動量分布関数
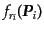 に等しい.なぜなら,領域Dの適
当な時刻一定面
に等しい.なぜなら,領域Dの適
当な時刻一定面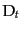 において量子状態
において量子状態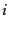 の占める位相体積は
の占める位相体積は
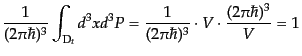 |
(I.2.62) |
となるからである.この分布関数を省略して
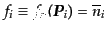 のような記法を用いる.こうして,反応
のような記法を用いる.こうして,反応
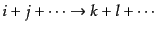 が領域D内で発生する確率は
が領域D内で発生する確率は
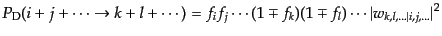 |
(I.2.63) |
で与えられる.
さて,ボルツマン方程式の衝突項は,位相空間素片
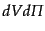 中における粒子
数の,アフィンパラメータあたりの変化を知ることにより式(9.2.35)か
ら得られる.そこで,まず領域Dの中で量子状態
中における粒子
数の,アフィンパラメータあたりの変化を知ることにより式(9.2.35)か
ら得られる.そこで,まず領域Dの中で量子状態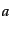 の数がどれだけ変化するか
の期待値
の数がどれだけ変化するか
の期待値
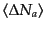 を考える.これは終状態に
を考える.これは終状態に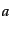 が入っているプロ
セスの発生確率から始状態に
が入っているプロ
セスの発生確率から始状態に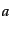 が入っているプロセスの発生確率を引いたも
ので与えられる.それは式(9.2.62)の確率を用いて
が入っているプロセスの発生確率を引いたも
ので与えられる.それは式(9.2.62)の確率を用いて
| |
|
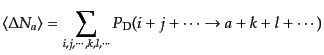 |
|
| |
|
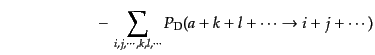 |
(I.2.64) |
となる.領域Dの静止座標系
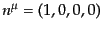 において,領域D中で量子状
態
において,領域D中で量子状
態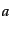 が占める不変位相体積
が占める不変位相体積
 は
は となる.
また,アフィンパラメータ
となる.
また,アフィンパラメータ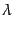 は
は
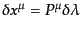 を満たすので,この量子状態のアフィンパラメータ間隔
を満たすので,この量子状態のアフィンパラメータ間隔
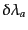 はエネルギー
はエネルギー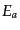 および領域Dの座標時間間隔
および領域Dの座標時間間隔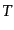 と
と
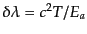 の関係にある.したがって,式(9.2.35)
を量子状態
の関係にある.したがって,式(9.2.35)
を量子状態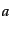 の不変位相体積で積分することにより,次のように衝突項が求
まる.
の不変位相体積で積分することにより,次のように衝突項が求
まる.
これを連続表示に戻せば,
となる.ここで,
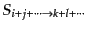 は反応
は反応
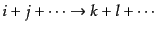 における不変規格化された連続表示での
S行列要素を表す.エネルギー運動量保存により式(8.6.351)で不変散
乱振幅が定義されるが,これを用いれば,式(8.6.352)と同様にして
における不変規格化された連続表示での
S行列要素を表す.エネルギー運動量保存により式(8.6.351)で不変散
乱振幅が定義されるが,これを用いれば,式(8.6.352)と同様にして
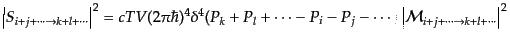 |
(I.2.67) |
となる.こうして衝突項の一般的な形は
である.相互作用のラグランジアンから,着目する相互作用プロセスの不変散
乱振幅
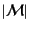 が計算されれば、衝突項が求まることになる.また,分布
関数
が計算されれば、衝突項が求まることになる.また,分布
関数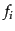 などは領域Dにおける粒子
などは領域Dにおける粒子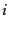 の運動量の分布を表していたが,マク
ロな見地からは場所と時間,すなわち時空座標
の運動量の分布を表していたが,マク
ロな見地からは場所と時間,すなわち時空座標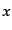 の関数となり,通常の分布
関数
の関数となり,通常の分布
関数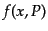 を表すことになる.
を表すことになる.
一般的な衝突項の形はわかったが,いくつかの特別な場合を以下に与えておく.
まず,相互作用に時間反転対称性があるとき,
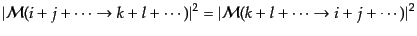 |
(I.2.69) |
が成り立つ.また、量子統計は密度が希薄な極限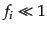 において古典統
計に帰着し,フェルミ粒子の場合のブロッキング因子
において古典統
計に帰着し,フェルミ粒子の場合のブロッキング因子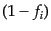 やボース粒子
の場合の誘導因子
やボース粒子
の場合の誘導因子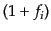 の効果はなく
の効果はなく
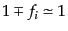 となる。した
がって、これら2つの条件が成り立つときには,衝突項の表式は簡単化して,
となる。した
がって、これら2つの条件が成り立つときには,衝突項の表式は簡単化して,
| |
|
![$\displaystyle C[f] =
\frac{1}{2c}
\int d\Pi_i d\Pi_j \cdots d\Pi_k d\Pi_l \cdots
(2\pi\hbar)^4 \delta^4(P_i+P_j+\cdots-P_a-P_k-P_l-\cdots)$](img2656.png) |
|
| |
|
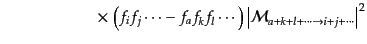 |
(I.2.70) |
となる.
密度が一様等方な膨張宇宙におけるボルツマン方程式を考える.この場合,分
布関数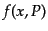 は3次元運動量の方向によらないのでその絶対値
は3次元運動量の方向によらないのでその絶対値
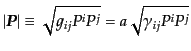 |
(I.2.71) |
のみの関数となる.一様等方宇宙のクリストッフェル記号は式(3.1.5)
で与えられ,これによりボルツマン方程式(9.2.36)の左辺は
![$\displaystyle L[f] = \frac{E}{c^2} \frac{\partial f}{\partial t} - \frac{2}{c^2}\frac{\dot{a}}{a} E P^i \frac{\partial f}{\partial P^i}$](img2659.png) |
(I.2.72) |
となる.ただし,空間曲率はゼロとして直交座標を取れるものとし,
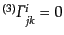 とおいた.上で注意したように分布関数は
とおいた.上で注意したように分布関数は
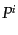 の方向にはよらないから左辺第2項は
の方向にはよらないから左辺第2項は
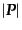 の微分で表すことがで
きる.ここで注意しなければならないことは,
の微分で表すことがで
きる.ここで注意しなければならないことは,
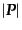 と
と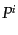 の関係がス
ケール因子
の関係がス
ケール因子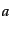 を通じて時間に依存していることである.したがって
を通じて時間に依存していることである.したがって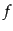 を
を
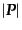 の関数とみなすと,式(9.2.72)の時間に関する偏微分の
項も変更を受ける.すなわち,独立変数をあらわに区別するために
の関数とみなすと,式(9.2.72)の時間に関する偏微分の
項も変更を受ける.すなわち,独立変数をあらわに区別するために
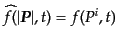 とおくと,
とおくと,
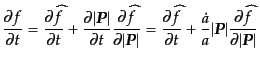 |
(I.2.73) |
となる.また,第2項の微分の部分の計算は直線的で,
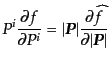 |
(I.2.74) |
となる.以後は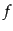 は
は
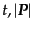 の関数であるものとして時間の偏微分は
の関数であるものとして時間の偏微分は
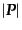 を固定した微分であるものと了解し,上につけたハットは省略す
る.この了解の下で
を固定した微分であるものと了解し,上につけたハットは省略す
る.この了解の下で
![$\displaystyle L[f] = \frac{E}{c^2} \left( \frac{\partial f}{\partial t} - \frac...
...h$P$}}\vert \frac{\partial f}{\partial \vert{\mbox{\boldmath$P$}}\vert} \right)$](img2666.png) |
(I.2.75) |
でかける.さらにまた,一様等方宇宙で衝突項も
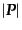 と時間のみの関
数
と時間のみの関
数
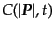 となるので,一様等方膨張宇宙のボルツマン方程式は
となるので,一様等方膨張宇宙のボルツマン方程式は
![$\displaystyle \frac{\partial f}{\partial t} - H \vert{\mbox{\boldmath$P$}}\vert \frac{\partial f}{\partial \vert{\mbox{\boldmath$P$}}\vert} = \frac{c^2}{E} C[f]$](img2668.png) |
(I.2.76) |
となるI2.ただし,
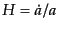 は時間依存するハッブ
ルパラメータである.
は時間依存するハッブ
ルパラメータである.
一様等方宇宙の物理量としては,ある粒子種の数密度が重要な役割を果たす.
一様等方宇宙では粒子数密度と相対論的分布関数の関係(9.1.5)は
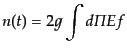 |
(I.2.77) |
となる.ただし,
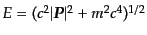 であり,またスピ
ンなど内部自由度のみ異なる粒子は区別しない数密度を考え,その内部自由度
を
であり,またスピ
ンなど内部自由度のみ異なる粒子は区別しない数密度を考え,その内部自由度
を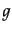 とした.上のボルツマン方程式に
とした.上のボルツマン方程式に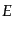 をかけてから
をかけてから
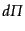 積分を行い,
右辺第2項に部分積分を施せば,数密度の時間発展を記述する方程式
積分を行い,
右辺第2項に部分積分を施せば,数密度の時間発展を記述する方程式
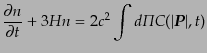 |
(I.2.78) |
が得られる.左辺第2項は物理的体積あたりの粒子数密度が膨張にともなって
薄まっていく効果を表している.共動体積あたりの粒子数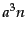 にはそのよ
うな効果は存在しない.このことは上の式を次のように変形してみればよくわ
かる:
にはそのよ
うな効果は存在しない.このことは上の式を次のように変形してみればよくわ
かる:
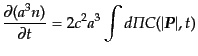 |
(I.2.79) |
この式において左辺は共動体積あたりの粒子の数の変化を表すので,右辺はそ
の体積中で,反応により粒子が生成される割合を表すことになる.
Footnotes
- ...
反応によりその量子状態の粒子の生成確率が大きくなることを表しているI1
- この現象は放射場においては誘導放射(stimulated emission)とし
て知られ,レーザーやメーザーの原理になっている.
- ...
となるI2
- 文献によってはこの式の右辺を衝突項
![$ C[f]$](img2555.png) とする記法を用
いることもあるので注意.
とする記法を用
いることもあるので注意.





次へ: 膨張宇宙における光子と電子の相互作用
上へ: 相対論的運動学
前へ: 相対論的分布関数と巨視的変数
目次
索引
All rights reserved © T.Matsubara 2004-2010
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11
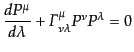
![]() は,ある座標系における空間
方向の3次元不変体積
は,ある座標系における空間
方向の3次元不変体積![]() と,これに垂直な方向を向いた長さ
と,これに垂直な方向を向いた長さ![]() の時間的間
隔分との積
の時間的間
隔分との積![]() で与えられる.いま,ベクトル
で与えられる.いま,ベクトル![]() を、粒子の世界線が
この微小体積中と交わる長さと同じ長さを持ち,粒子の世界線に沿った方向を
持つようなものとする.すると,長さ
を、粒子の世界線が
この微小体積中と交わる長さと同じ長さを持ち,粒子の世界線に沿った方向を
持つようなものとする.すると,長さ![]() はこのベクトルの
はこのベクトルの![]() に垂直な方向
の成分となる.そこで,
に垂直な方向
の成分となる.そこで,![]() を
を![]() に垂直な,時間的単位ベクトルとし,
また微小体積中での粒子のアフィンパラメータの幅を
に垂直な,時間的単位ベクトルとし,
また微小体積中での粒子のアフィンパラメータの幅を![]() とすると,
とすると,
![]() を横切る粒子のうち,
運動量が
を横切る粒子のうち,
運動量が
![]() の範囲にあるものの数を
の範囲にあるものの数を![]() とする.微小体積
とする.微小体積
![]() 中に
ある粒子4元流束は
中に
ある粒子4元流束は
![]() 中の粒子の数
は粒子の測地線に沿って一定となる.このときには式(9.2.32)はゼロに
なり,したがって,次の相対論的なリュービル方程式(Liouville
equation)
中の粒子の数
は粒子の測地線に沿って一定となる.このときには式(9.2.32)はゼロに
なり,したがって,次の相対論的なリュービル方程式(Liouville
equation)
![]() が消えず,位相空間素片中で粒子
が出入りすることになる.粒子の運動に沿ってアフィンパラメータが
が消えず,位相空間素片中で粒子
が出入りすることになる.粒子の運動に沿ってアフィンパラメータが
![]() だけ変化する間の,
だけ変化する間の,
![]() 中の粒子数が変化を
中の粒子数が変化を
![]() ,また式
(9.1.14)で与えられるエネルギー運動量テンソル
,また式
(9.1.14)で与えられるエネルギー運動量テンソル
![]() の発散に
関して,次の式が成り立つ.
の発散に
関して,次の式が成り立つ.
![]() の生成消滅演算子を
の生成消滅演算子を
![]() ,
,
![]() と書くことにする.ここで,添字の
と書くことにする.ここで,添字の![]() はこの粒子の種類とさ
らに内部自由度の違いも区別するものとする.例えば,スカラー粒子,スピン
はこの粒子の種類とさ
らに内部自由度の違いも区別するものとする.例えば,スカラー粒子,スピン
![]() の電子,スピン
の電子,スピン![]() の電子,偏極
の電子,偏極
![]() の光子,偏極
の光子,偏極
![]() の光子,などはすべて異なる
の光子,などはすべて異なる![]() に属する.これらはまとめて,次の(反)
交換関係を満たす:
に属する.これらはまとめて,次の(反)
交換関係を満たす:
![]() にある粒子が
にある粒子が![]() 個ずつ存在する状態ベクトルは
個ずつ存在する状態ベクトルは
![]() を考える.はじめの仮定に基づき,領域Dは十分小さく、この
中では時空の曲率が無視できて平坦時空の場の量子論が適用できるものとする.
また,同時に衝突の時空間隔よりは十分大きく,漸近場による散乱理論が適用
できるものとする.領域Dの体積を
を考える.はじめの仮定に基づき,領域Dは十分小さく、この
中では時空の曲率が無視できて平坦時空の場の量子論が適用できるものとする.
また,同時に衝突の時空間隔よりは十分大きく,漸近場による散乱理論が適用
できるものとする.領域Dの体積を![]() , 時間間隔を
, 時間間隔を![]() として,この体積を上
で運動量の離散化に用いた体積と同一視する.いま,始状態として多粒子系の
状態ベクトル
として,この体積を上
で運動量の離散化に用いた体積と同一視する.いま,始状態として多粒子系の
状態ベクトル
![]() 積の和
で与えられ,さらにウィックの定理により正規順序積の和に展開されるから,
一般的に連続表示において
積の和
で与えられ,さらにウィックの定理により正規順序積の和に展開されるから,
一般的に連続表示において
![]() に関係するもののみがS行列
演算子とペアを作る.なぜなら,ある量子状態にある始状態の粒子が,相互作
用の結果として同じ量子状態の終状態として表れるファインマン図は,始状態
がそのまま終状態につながっているようなファインマン図よりも摂動の次数が
高くなるからである.したがって,摂動の最低次の近似では展開
(9.2.58)の一種類の項だけがS行列要素に寄与し,始状態および終状
態の粒子の並び替えの自由度を考慮して
に関係するもののみがS行列
演算子とペアを作る.なぜなら,ある量子状態にある始状態の粒子が,相互作
用の結果として同じ量子状態の終状態として表れるファインマン図は,始状態
がそのまま終状態につながっているようなファインマン図よりも摂動の次数が
高くなるからである.したがって,摂動の最低次の近似では展開
(9.2.58)の一種類の項だけがS行列要素に寄与し,始状態および終状
態の粒子の並び替えの自由度を考慮して
![]() が与え
られたとき,ある終状態
が与え
られたとき,ある終状態
![]() に反応する確率を表している.ここで,
始状態において占められている粒子数
に反応する確率を表している.ここで,
始状態において占められている粒子数
![]() につ
いての統計平均をとれば,この反応が起きる確率を与えることになる.統計平
均をとるときには異なる量子状態間に相関はなく,
につ
いての統計平均をとれば,この反応が起きる確率を与えることになる.統計平
均をとるときには異なる量子状態間に相関はなく,
![]() は各量子状態の粒子数の平均値
は各量子状態の粒子数の平均値
![]() に置き換えられることになる.平均値
に置き換えられることになる.平均値
![]() は領域Dにおける粒子
は領域Dにおける粒子
![]() の運動量分布関数
の運動量分布関数
![]() に等しい.なぜなら,領域Dの適
当な時刻一定面
に等しい.なぜなら,領域Dの適
当な時刻一定面![]() において量子状態
において量子状態![]() の占める位相体積は
の占める位相体積は
![]() 中における粒子
数の,アフィンパラメータあたりの変化を知ることにより式(9.2.35)か
ら得られる.そこで,まず領域Dの中で量子状態
中における粒子
数の,アフィンパラメータあたりの変化を知ることにより式(9.2.35)か
ら得られる.そこで,まず領域Dの中で量子状態![]() の数がどれだけ変化するか
の期待値
の数がどれだけ変化するか
の期待値
![]() を考える.これは終状態に
を考える.これは終状態に![]() が入っているプロ
セスの発生確率から始状態に
が入っているプロ
セスの発生確率から始状態に![]() が入っているプロセスの発生確率を引いたも
ので与えられる.それは式(9.2.62)の確率を用いて
が入っているプロセスの発生確率を引いたも
ので与えられる.それは式(9.2.62)の確率を用いて
![]() は3次元運動量の方向によらないのでその絶対値
は3次元運動量の方向によらないのでその絶対値
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11