




次へ: 散乱断面積の計算例
上へ: 場の量子化と粒子の相互作用
前へ: 自由場の量子化
目次
索引
Subsections
ここまでの議論から明らかなように、量子場とは無限自由度の量子力学である。
したがって、通常の量子力学と同様、場の理論においての量子系の時間発展の
記述に対し、シュレーディンガー描像 (Schrödinger picture)とハイゼンベルグ描像 (Heisenberg picture)という異なる見方がある。
シュレーディンガー描像では、場のハミルトニアン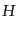 が与えられたときに、
状態ベクトル
が与えられたときに、
状態ベクトル
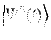 が時間発展し、その従う微分方程式は
シュレーディンガー方程式
が時間発展し、その従う微分方程式は
シュレーディンガー方程式
 |
(H.6.272) |
である。ここで、上添字のSはシュレーディンガー描像であることを明示す
るために付けてある。このとき、物理量に対応する演算子
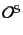 は陽に時間に依存することはない。このような量子的時間発展の表示をシュレーディンガー表示(Schrödinger representation)という。
は陽に時間に依存することはない。このような量子的時間発展の表示をシュレーディンガー表示(Schrödinger representation)という。
一方、ハイゼンベルグ描像では、状態ベクトルは固定されたまま時間発展せず、
そのかわり系の時間発展は物理量に対応する演算子
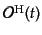 の
時間発展によって表される。ここで、上添字のHはハイゼンベルグ描像を明示
するためにつけた。そのような演算子はすべて場の正準変数
の
時間発展によって表される。ここで、上添字のHはハイゼンベルグ描像を明示
するためにつけた。そのような演算子はすべて場の正準変数
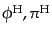 の関数であり、その満たす微分方程式はハイゼンベルグ方程式
の関数であり、その満たす微分方程式はハイゼンベルグ方程式
![$\displaystyle \frac{\partial\phi^{\rm H}}{\partial t} = \frac{i}{\hbar} \left[H...
...{\partial\pi^{\rm H}}{\partial t} = \frac{i}{\hbar} \left[H, \pi^{\rm H}\right]$](img1960.png) |
(H.6.273) |
である。このとき、状態ベクトル
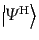 は陽に時間に依存す
ることはない。このような量子的時間発展の表示をハイゼンベルグ表示
(Heisenberg representation)という。
は陽に時間に依存す
ることはない。このような量子的時間発展の表示をハイゼンベルグ表示
(Heisenberg representation)という。
量子化の基準時刻を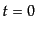 として、そのときの状態ベクトルを
として、そのときの状態ベクトルを
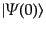 とする。すると、シュレーディンガー表示で
の時間発展の式(8.6.272)の解は形式的に、
とする。すると、シュレーディンガー表示で
の時間発展の式(8.6.272)の解は形式的に、
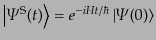 |
(H.6.274) |
と表せる。また、同じ基準時刻での演算子を
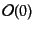 とすると、ハイゼ
ンベルグ表示での時間発展の式(8.6.273)の解は形式的に
とすると、ハイゼ
ンベルグ表示での時間発展の式(8.6.273)の解は形式的に
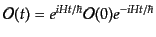 |
(H.6.275) |
というユニタリ変換となることがわかる。すると演算子の期待値は表示によら
ず
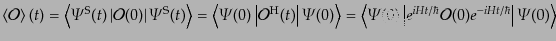 |
(H.6.276) |
となる。
自由場の時間発展を考えよう。まず、シュレーディンガー表示の場合、フォッ
ク空間の基底である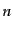 粒子状態が時間発展し、
粒子状態が時間発展し、
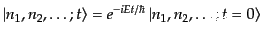 |
(H.6.277) |
となる。ここで、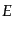 は
は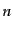 粒子状態のエネルギー固有値である。したがって、
粒子状態のエネルギー固有値である。したがって、
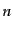 粒子状態は時間発展しても位相因子が変化するだけである。位相因子は観
測量に対応する確率振幅には無関係であり、依然時間発展した状態は依然
粒子状態は時間発展しても位相因子が変化するだけである。位相因子は観
測量に対応する確率振幅には無関係であり、依然時間発展した状態は依然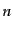 粒子状態のままである。したがって、自由場では粒子数の変化は起こらない。
粒子状態のままである。したがって、自由場では粒子数の変化は起こらない。
ハイゼンベルグ表示では場の演算子が時間発展し、
![$\displaystyle \phi(t,{\mbox{\boldmath$x$}}) = e^{iHt/\hbar} \phi(0,{\mbox{\bold...
...size\boldmath$k$}}\cdot{\mbox{\scriptsize\boldmath$x$}}} \right] e^{-iHt/\hbar}$](img1970.png) |
(H.6.278) |
となる。この最後の表式は実スカラー場の場合を例に取って展開しているが、
他の場への拡張は全く自明である。る。ここで任意の演算子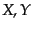 についての
恒等式H8
についての
恒等式H8
![$\displaystyle e^{X} Y e^{-X} = Y + \left[X,Y\right] + \frac12 \left[X,\left[X,Y...
...]\right] + \frac{1}{3!} \left[X,\left[X,\left[X,Y\right]\right]\right] + \cdots$](img1973.png) |
(H.6.279) |
と交換関係
![\begin{displaymath}\begin{array}{l} \left[H, a({\mbox{\boldmath$k$}})\right] = -...
...k$}})\right] = k^0 a^\dagger({\mbox{\boldmath$k$}}) \end{array}\end{displaymath}](img1974.png) |
(H.6.280) |
を使えば、生成消滅演算子の時間発展が、
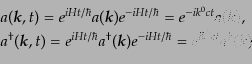 |
(H.6.281) |
となることがわかる。したがって、場の演算子の時間発展は、実スカラー場の
場合
![$\displaystyle \phi(x) = \int \frac{d^3k}{(2\pi)^3 2k^0} \left[a({\mbox{\boldmath$k$}}) e^{ikx} + a^\dagger({\mbox{\boldmath$k$}}) e^{-ikx} \right]$](img1821.png) |
(H.6.282) |
となり、クライン・ゴルドン方程式を満たす古典場の解の係数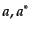 を演算
子
を演算
子
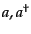 に置き換えたものと全く同じ形である。他の場の場合も全く
同様に、運動方程式を満たす古典場の展開における係数を生成消滅演算子に置
き換えたものと全く同じものとなる。このハイゼンベルグ表示では、場の生成
消滅演算子は各時刻ごとに異なるので、フォック基底も時刻ごとに構成される
ことになる。
に置き換えたものと全く同じ形である。他の場の場合も全く
同様に、運動方程式を満たす古典場の展開における係数を生成消滅演算子に置
き換えたものと全く同じものとなる。このハイゼンベルグ表示では、場の生成
消滅演算子は各時刻ごとに異なるので、フォック基底も時刻ごとに構成される
ことになる。
さて、相互作用のある場合の時間発展はシュレーディンガー表示とハイゼンベ
ルグ表示の中間的な表示である、相互作用表示 (interaction
representation)が便利である。この表示では、まずハミルトニアンを自由部
分と相互作用部分に分けて、
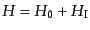 |
(H.6.283) |
と書けるものとする。ここで、基準時刻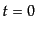 でシュレーディンガー表示の場
の演算子に一致し、かつ自由ハミルトニアンによって時間発展するような次の
場の演算子
でシュレーディンガー表示の場
の演算子に一致し、かつ自由ハミルトニアンによって時間発展するような次の
場の演算子
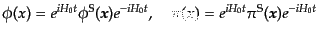 |
(H.6.284) |
を定義する。ここで添字のSはシュレーディンガー表示の演算子を表している。
すると、場の任意の多項式で表される演算子
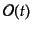 も同様の時間発展
も同様の時間発展
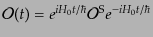 |
(H.6.285) |
をし、これは自由場のハイゼンベルグ方程式を満たす:
![$\displaystyle \frac{\partial{\cal O}}{\partial t} = \frac{i}{\hbar} \left[H_0, {\cal O}\right]$](img1982.png) |
(H.6.286) |
相互作用表示における状態ベクトル
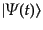 の時間発展は、場の演算
子の期待値が表示に依らないという条件により決められる。式
(8.6.276)から、その条件は
の時間発展は、場の演算
子の期待値が表示に依らないという条件により決められる。式
(8.6.276)から、その条件は
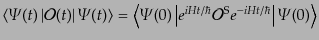 |
(H.6.287) |
である。すなわち、相互作用表示では、
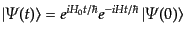 |
(H.6.288) |
である。ここで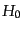 と
と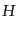 は一般に非可換であることに注意する。これを時間
微分して従う微分方程式を求めると、
は一般に非可換であることに注意する。これを時間
微分して従う微分方程式を求めると、
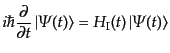 |
(H.6.289) |
となる。相互作用ハミルトニアンが場の演算子の多項式であれば、その時間発
展は
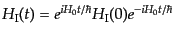 |
(H.6.290) |
となることを用いている。つまり、相互作用表示では、状態ベクトルは全ハミ
ルトニアンの相互作用部分をハミルトニアンとするシュレーディンガー方程式
にしたがって時間発展する。自由場に対しての相互作用表示はハイゼンベルグ
表示に一致することは明らかである。
粒子同士が衝突する場合を考えよう。衝突においては、粒子同士の相互作用は
ごく限られた時空内でのみ起こる。すると、衝突の十分以前
 、および十分以後
、および十分以後
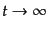 では相互作用のない、自由
な状態になっているので、場は自由ハイゼンベルグ演算子となっているであろ
う。この仮定は漸近条件と呼ばれる。ただし、ここではより厳密な議論を避け、
直観的な説明をすることにする。衝突の十分以前の自由ハイゼンベルグ演算子
では相互作用のない、自由
な状態になっているので、場は自由ハイゼンベルグ演算子となっているであろ
う。この仮定は漸近条件と呼ばれる。ただし、ここではより厳密な議論を避け、
直観的な説明をすることにする。衝突の十分以前の自由ハイゼンベルグ演算子
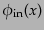 の生成消滅演算子を
の生成消滅演算子を
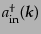 ,
,
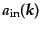 とし、また、衝突の十分以後の自由ハイゼンベルグ演
算子
とし、また、衝突の十分以後の自由ハイゼンベルグ演
算子
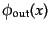 の生成消滅演算子を
の生成消滅演算子を
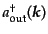 ,
,
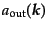 とする。すると、それぞれのフォッ
ク基底は
とする。すると、それぞれのフォッ
ク基底は
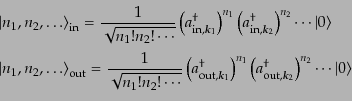 |
(H.6.291) |
と構成される。また、これらinおよびout状態のフォック基底がそれぞれ張る
フォック空間は、もとのハイゼンベルグ場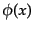 のフォック空間と一致す
ること、すなわち、漸近的完全性を仮定する。
のフォック空間と一致す
ること、すなわち、漸近的完全性を仮定する。
in状態の生成演算子を用いて構成される状態
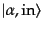 から、
out状態の生成演算子を用いて構成される状態
から、
out状態の生成演算子を用いて構成される状態
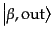 へと相
互作用の結果変化する過程を考え、次の量
へと相
互作用の結果変化する過程を考え、次の量
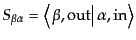 |
(H.6.292) |
を
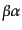 成分とする行列のことをS行列 (S matrix)という。こ
れは粒子の衝突・散乱における確率振幅を与える重要な量である。さらに、S
行列演算子
成分とする行列のことをS行列 (S matrix)という。こ
れは粒子の衝突・散乱における確率振幅を与える重要な量である。さらに、S
行列演算子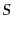 を
を
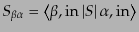 |
(H.6.293) |
となるように定義する。ここで、フォック基底の正規直交性と漸近的完全性の
仮定より、
| |
|
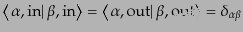 |
(H.6.294) |
| |
|
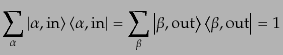 |
(H.6.295) |
である。これらにより、S行列のユニタリ性
| |
|
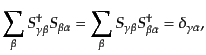 |
(H.6.296) |
| |
|
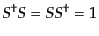 |
(H.6.297) |
が容易に示され、また、
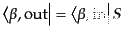 |
(H.6.298) |
であることがわかる。この式(8.6.298)において、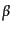 状態として
状態として
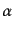 状態にもう一つ粒子を加えた状態
状態にもう一つ粒子を加えた状態
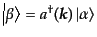 をとれば、漸近場の関係として、
をとれば、漸近場の関係として、
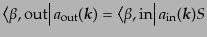 |
(H.6.299) |
となり、ここで式(8.6.298)と完全性(8.6.295)を使えば、
 |
(H.6.300) |
であることがわかる。したがって場の演算子についても同様の
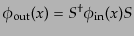 |
(H.6.301) |
という関係がある。
S行列のより具体的な形を求めよう。そのためにまず、ある時刻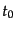 を基準
としたときの時刻
を基準
としたときの時刻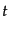 の状態ベクトルの形を求めてみると、相互作用表示の状
態ベクトルの時間発展の式(8.6.288) により、
の状態ベクトルの形を求めてみると、相互作用表示の状
態ベクトルの時間発展の式(8.6.288) により、
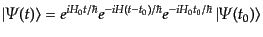 |
(H.6.302) |
というユニタリ変換となる。このユニタリ変換の演算子を
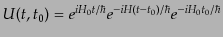 |
(H.6.303) |
とかく。この演算子は次の性質を満たす:
| |
|
 |
(H.6.304) |
| |
|
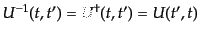 |
(H.6.305) |
| |
|
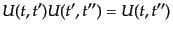 |
(H.6.306) |
このとき、場の演算子の相互作用表示における期待値をかくと、
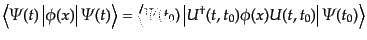 |
(H.6.307) |
となる。すると、状態ベクトル
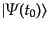 は固定されているとき、
は固定されているとき、
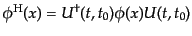 |
(H.6.308) |
は基準時刻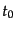 で相互作用表示の演算子
で相互作用表示の演算子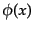 に一致するハイゼンベルグ
表示の演算子であることになる。そこでこれを逆に見れば、ハイゼンベルグ演
算子
に一致するハイゼンベルグ
表示の演算子であることになる。そこでこれを逆に見れば、ハイゼンベルグ演
算子
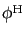 が与えられたとき、
が与えられたとき、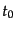 の選び方に応じたいろいろな相
互作用表示が定義できることになる。すると、
の選び方に応じたいろいろな相
互作用表示が定義できることになる。すると、
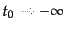 お
よび
お
よび
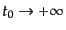 に対応する相互作用表示の演算子はそれぞれ
漸近場
に対応する相互作用表示の演算子はそれぞれ
漸近場
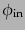 ,
,
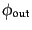 に等しい。したがって、
に等しい。したがって、
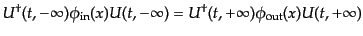 |
(H.6.309) |
となり、さらに
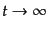 としてやると、
としてやると、
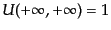 としてやってH9、式(8.6.301)と比べることにより、S
行列が
としてやってH9、式(8.6.301)と比べることにより、S
行列が
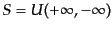 |
(H.6.310) |
と対応していることがわかる。さらに、式(8.6.302)により、
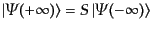 |
(H.6.311) |
であることがわかる。
一般の場合にS行列を求めることは極めて難しいが、相互作用が強くない場合
には相互作用項に含まれるパラメータを微小量として展開することにより求め
ることができる。相互作用表示における状態ベクトルの発展方程式
(8.6.289)を時刻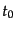 から
から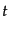 まで積分すると、
まで積分すると、
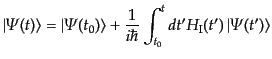 |
(H.6.312) |
となる。これを逐次近似によって状態ベクトル
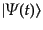 について解け
ば、
について解け
ば、
![$\displaystyle \left\vert {\mit\Psi}(t) \right\rangle = \left[ 1 + \frac{1}{i\hb...
...}(t_1) H_{\rm I}(t_2) + \cdots \right] \left\vert {\mit\Psi}(t_0) \right\rangle$](img2029.png) |
(H.6.313) |
と表せて、相互作用項について展開した形を得る。このままではまだ不便な形
をしているので、ダイソンにより導入された時間順序積 (time-ordered
product)、あるいはT積 (T-product)を使う。複数の時刻
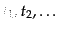 があるとき、これを値の大きい順に並び替えて、
があるとき、これを値の大きい順に並び替えて、
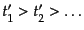 となったとする。このとき演算子のT積は
となったとする。このとき演算子のT積は
![$\displaystyle {\rm T}\left[ H_{\rm I}(t_1) H_{\rm I}(t_2) \cdots \right] = H_{\rm I}(t_1') H_{\rm I}(t_2') \cdots$](img2032.png) |
(H.6.314) |
で定義される。すなわち複数の演算子から時間の順序に並び替えた積を与える
ようなものである。この表記を用いると、展開形(8.6.303)の 次の
積分は、
次の
積分は、
となる。ここで、第一の等式は積分範囲とT積に定義から明らかで、第二の等
式はT積の中身が
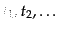 について対称であることから積分範囲を
広げて対称因子で割ることにより導ける。
について対称であることから積分範囲を
広げて対称因子で割ることにより導ける。
式(8.6.309)と(8.6.311)から、極限
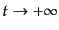 ,
,
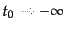 をとれば式(8.6.309)よりS行列を与える
ことがわかり、
をとれば式(8.6.309)よりS行列を与える
ことがわかり、
となる。これをS行列に対するダイソンの公式という。最後の2つの表式での
積分範囲は全時空である。この式を用いれば、相互作用ハミルトニアンに含ま
れるパラメータを摂動として、摂動論によってS行列を求めることができるこ
とになる。
ラグランジアン密度の相互作用項
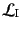 が場の微分を含まない,
すなわち相互作用が微分結合を含まない場合,共役変数
が場の微分を含まない,
すなわち相互作用が微分結合を含まない場合,共役変数
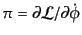 は相互作用項に無関係に決まるから,
は相互作用項に無関係に決まるから,
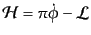 により求められる相互作用ハミルトニアン
密度は
により求められる相互作用ハミルトニアン
密度は
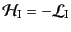 となる.したがって,この
ダイソンの公式はこの場合,
となる.したがって,この
ダイソンの公式はこの場合,
![$\displaystyle S = {\rm T} \left[\exp \left(\frac{i}{\hbar c}\int d^4x {\cal L}_{\rm I}(x)\right) \right]$](img2045.png) |
(H.6.317) |
と表すことができる.実は,相互作用がくりこみ可能な場合には,微分結合を
含む場合でも,式(8.6.317)はT積を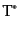 積に置き換えれば
依然成立することが知られている.ここで
積に置き換えれば
依然成立することが知られている.ここで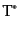 積とは時間微分をT積の
左側に出してしまったもので,
積とは時間微分をT積の
左側に出してしまったもので,
![$\displaystyle {\rm T}^*\left[\frac{\partial A(x)}{\partial x^0} B(y)\right] \equiv \frac{\partial}{\partial x^0}{\rm T}\left[A(x)B(y)\right]$](img2047.png) |
(H.6.318) |
のように定義される.
上で見たように、S行列を摂動論によって求めるためには、場の積のT積を求め
る必要がある。これを行うのに、極めて有用なものがウィックの定理
(Wick theorem)である。この定理の意味するところを例によって示せば、任
意の場
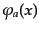 について、
について、
| |
|
![$\displaystyle {\rm T}\left[\varphi_1(x_1)\varphi_2(x_2)\right] =
: \varphi_1(...
...rt {\rm T}\left[\varphi_1(x_1)\varphi_2(x_2)\right] \right\vert 0 \right\rangle$](img2048.png) |
(H.6.319) |
| |
|
![$\displaystyle {\rm T}\left[\varphi_1\varphi_2\varphi_3\right] =
:\varphi_1\va...
...0 \left\vert {\rm T}\left[\varphi_2\varphi_3\right] \right\vert 0 \right\rangle$](img2049.png) |
|
| |
|
![$\displaystyle \qquad\qquad \pm
:\varphi_2:
\left\langle 0 \left\vert {\rm T}\...
...0 \left\vert {\rm T}\left[\varphi_1\varphi_2\right] \right\vert 0 \right\rangle$](img2050.png) |
(H.6.320) |
| |
|
![$\displaystyle {\rm T}\left[\varphi_1\varphi_2\varphi_3
\varphi_4\right] =
:\varphi_1\varphi_2\varphi_3\varphi_4:$](img2051.png) |
|
| |
|
![$\displaystyle \qquad\qquad +
\left\{
:\varphi_1\varphi_2:
\left\langle 0 \...
...varphi_3\varphi_4\right] \right\vert 0 \right\rangle +
{\rm sym.(6)}
\right\}$](img2052.png) |
|
| |
|
![$\displaystyle \qquad\qquad +
\left\{
\left\langle 0 \left\vert {\rm T}\left...
...varphi_3\varphi_4\right] \right\vert 0 \right\rangle +
{\rm sym.(2)}
\right\}$](img2053.png) |
(H.6.321) |
などとなる。2番目以降の式の引数は省略した。ここで、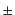 記号は、左辺の
演算子順序と直後の項の演算子順序がフェルミ粒子の交換を奇数回含むときに
記号は、左辺の
演算子順序と直後の項の演算子順序がフェルミ粒子の交換を奇数回含むときに
 をとり、そうでないときには
をとり、そうでないときには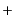 をとることを意味する。また、''
sym.(n)''は直前の項を場
をとることを意味する。また、''
sym.(n)''は直前の項を場
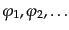 によって対称化(フェ
ルミ粒子同士は反対称化) する項で、直前の項を含めて全体で
によって対称化(フェ
ルミ粒子同士は反対称化) する項で、直前の項を含めて全体で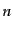 個の項とな
るものをを略記して表している。同様の公式が一般に
個の項とな
るものをを略記して表している。同様の公式が一般に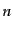 個の場のT積について
成り立つ。これを言葉で説明すると、まず、T積をとる
個の場のT積について
成り立つ。これを言葉で説明すると、まず、T積をとる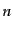 個の演算子からあら
ゆる可能なやり方で2つの演算子のペアを取り出す。このとき、いくつのペア
を取り出すかは任意である。その取り出したいくつかのペアを2点のT積の真
空期待値に置き換え、取り出されずに残った演算子は正規積にする。この操作
をあらゆる可能なペアの取り出し方について行って和をとると、それが
個の演算子からあら
ゆる可能なやり方で2つの演算子のペアを取り出す。このとき、いくつのペア
を取り出すかは任意である。その取り出したいくつかのペアを2点のT積の真
空期待値に置き換え、取り出されずに残った演算子は正規積にする。この操作
をあらゆる可能なペアの取り出し方について行って和をとると、それが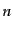 個
の演算子のT 積になっている。
個
の演算子のT 積になっている。
ここで、特別な記法として
![$\displaystyle \underwick{1}{<1\varphi_1(x_1) >1\varphi_2(x_2)} = \left\langle 0...
...rt {\rm T}\left[\varphi_1(x_1)\varphi_2(x_2)\right] \right\vert 0 \right\rangle$](img2055.png) |
(H.6.322) |
を定義し、ウィックの定理において、取り出したペアを2点のT積の真空期待値
に置き換える操作をウィックの縮約 (Wick contraction)と呼ぶ。この
記法によれば、例えば式(8.6.321)は
のように表される。ただし引数は省略した。また、上の記法で、フェルミ粒子
同士の交換を行ったときの符合の変化も折り込み済みであるとする。例えば右
辺第3項で、もし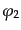 と
と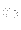 が両方ともフェルミ粒子を表すと
きには、
が両方ともフェルミ粒子を表すと
きには、
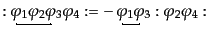 |
|
|
(H.6.324) |
のように解釈する。
ウィックの定理の証明は数学的帰納法によって比較的単調に証明できるが、こ
こでは省略する.詳細は文献H10 H11 を参照されたい.基本的に,左辺のT積を右辺第一項の正規積の順
序へ変形する際に必要な生成消滅演算子の順序交換から縮約が生じてくる.し
たがって,もしT積の内部にすでに正規順序積が含まれている場合には,その
部分については縮約は起こらない.例えば,
などのようである.こうして、ウィックの定理をダイソンの公式に使えばファ
インマン伝播関数を用いてS行列が摂動的に求まることになる.
このウィックの定理によれば、任意の次数の場のT積はウィックの縮約
(8.6.322) がわかれば計算できることになる。今、ミンコフスキー
時空を仮定しているので、時空の一様性からこの量は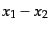 にしか依存し
ない。また、真空期待値で挟んでいることから、必ず生成演算子と消滅演算子
がペアで含まれなければならないので、スピノル場とベクトル場など、異なる
種類の場の縮約はゼロになる。そこで、ゼロでない縮約は実スカラー場、複素
スカラー場、ディラック場、実ベクトル場のそれぞれの場合に次のように書け
ることになる:
にしか依存し
ない。また、真空期待値で挟んでいることから、必ず生成演算子と消滅演算子
がペアで含まれなければならないので、スピノル場とベクトル場など、異なる
種類の場の縮約はゼロになる。そこで、ゼロでない縮約は実スカラー場、複素
スカラー場、ディラック場、実ベクトル場のそれぞれの場合に次のように書け
ることになる:
| |
|
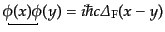 |
(H.6.326) |
| |
|
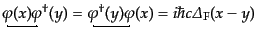 |
(H.6.327) |
| |
|
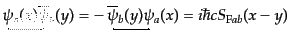 |
(H.6.328) |
| |
|
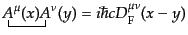 |
(H.6.329) |
ここで、
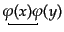 ,
,
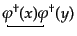 ,
,
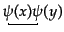 ,
,
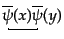 , なども
生成演算子と消滅演算子がペアで現れないため、ゼロになる。この関数
, なども
生成演算子と消滅演算子がペアで現れないため、ゼロになる。この関数
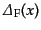 ,
,
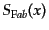 ,
,
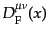 などを
それぞれの場に対するファインマン伝播関数 (Feynman propagator) と
いう。
などを
それぞれの場に対するファインマン伝播関数 (Feynman propagator) と
いう。
スカラー場の場合、2点のT 積は階段関数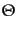 を用いて、
を用いて、
![$\displaystyle {\rm T}\left[\phi(x)\phi(y)\right] = \Theta(x^0-y^0)\phi(x)\phi(y) + \Theta(y^0-x^0)\phi(y)\phi(x)$](img2080.png) |
(H.6.330) |
と表せるから、その真空期待値は、式(8.5.228)を用いて
となる。最後の表式で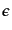 は正の無限小で、
は正の無限小で、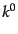 積分の極を
積分の極を
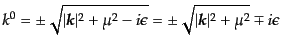 |
(H.6.332) |
のように実軸からずらす。これは図8.1の左
のような積分経路となっているが、
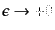 の極限では事
実上右の図のように、負の実軸上の極を下回りに、正の実軸上の極を上回りに
避けた経路を指定したことに等価である。
の極限では事
実上右の図のように、負の実軸上の極を下回りに、正の実軸上の極を上回りに
避けた経路を指定したことに等価である。
図 8.1:
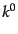 の積分経路
の積分経路
|
|
この式(8.6.331)の最後の式は、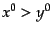 のとき図8.1の
下半面の半径無限大の半円で閉じると実軸上の積分のみ残り、
のとき図8.1の
下半面の半径無限大の半円で閉じると実軸上の積分のみ残り、
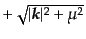 の極での留数のみ拾うので、直前の式の第一
項に等しくなる。逆に
の極での留数のみ拾うので、直前の式の第一
項に等しくなる。逆に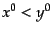 のときは上半面の半円で閉じることで直前
の式の第二項になる。
のときは上半面の半円で閉じることで直前
の式の第二項になる。
ファインマン伝播関数はしたがって、
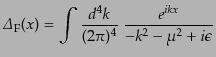 |
(H.6.333) |
と求まる。この形から明らかなように、ファインマン伝播関数はクライン・ゴ
ルドン方程式のグリーン関数の一つとなっている:
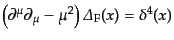 |
(H.6.334) |
複素スカラー場の場合は、式(8.6.331)の最初の式が、
となるが、その後の形は全く同じであり、ファインマン伝播関数の形も同じ形
(8.6.333)である。
ディラック場の場合は、
となるから、ファインマン伝播関数は式(8.4.167)を用いると、
と表される。
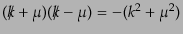 であ
ることから、この最後の形は記号的に
であ
ることから、この最後の形は記号的に
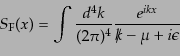 |
(H.6.338) |
と書かれることが多い。
ベクトル場の場合も偏極ベクトルの完全性(8.4.194)を使うことによ
り、ほとんど同様の計算を繰り返して、
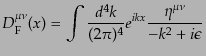 |
(H.6.339) |
を得る。
粒子の衝突などの反応が一度だけ起こるような場合に、その確率を求めるには
上で示したS行列を計算すれば十分であるが、実際問題としては多数の粒子が
反応した場合の反応確率を表す量を定義すると便利である。
まず、2つの粒子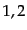 が衝突して、粒子
が衝突して、粒子
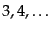 となるような散
乱過程
となるような散
乱過程
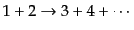 |
(H.6.340) |
を考える。粒子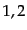 がそれぞれ多数の粒子からなるビームとなってお
互いに衝突するような状況を考えて、ビームの数密度がそれぞれ
がそれぞれ多数の粒子からなるビームとなってお
互いに衝突するような状況を考えて、ビームの数密度がそれぞれ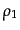 ,
,
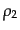 であるときに、相対速度
であるときに、相対速度
 で衝突するものとする。この
とき、体積
で衝突するものとする。この
とき、体積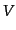 、時間
、時間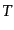 の時空内で衝突が
の時空内で衝突が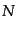 回起こったとする。この場合、
衝突回数は
回起こったとする。この場合、
衝突回数は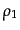 ,
, 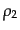 ,
,
 ,
, 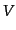 ,
, 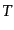 に比例することが
明らかであり、その比例係数は衝突反応過程に固有の量であり、断面積
(cross section)
に比例することが
明らかであり、その比例係数は衝突反応過程に固有の量であり、断面積
(cross section) 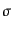 と呼ばれる。すなわち、
と呼ばれる。すなわち、
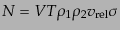 |
(H.6.341) |
で定義される。さらにまた、散乱された粒子
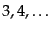 の状態、例えば運
動量や散乱方向などがある特別な微小範囲
の状態、例えば運
動量や散乱方向などがある特別な微小範囲
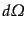 に含まれている数を
に含まれている数を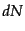 とするとき、
とするとき、
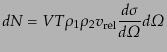 |
(H.6.342) |
で定義される
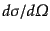 はこの状態への微分断面積
(differential cross section)と呼ばれる。
はこの状態への微分断面積
(differential cross section)と呼ばれる。
断面積の意味をより分かりやすくとらえるために、粒子 の静止系で考えて
みる。図8.2のように、粒子
の静止系で考えて
みる。図8.2のように、粒子 に向かって多数の粒子
に向かって多数の粒子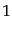 が相対速度
が相対速度
 で向かってくる。
で向かってくる。
このとき、仮に粒子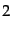 のまわりの面積
のまわりの面積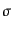 の中に入射した粒子がすべて
衝突すると考えてみる。するとあるひとつの粒子
の中に入射した粒子がすべて
衝突すると考えてみる。するとあるひとつの粒子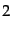 が、時間
が、時間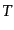 の間に粒子
の間に粒子
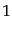 と衝突する回数は、図の円筒形の部分にある粒子
と衝突する回数は、図の円筒形の部分にある粒子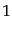 の数と同じで、
の数と同じで、
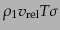 となる。また粒子
となる。また粒子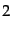 は体積
は体積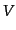 中に
中に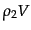 個存在するので、都合、
個存在するので、都合、
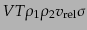 回の衝突が
起きることになって式(8.6.341)に一致する。この例は、剛体球どう
しの衝突のように粒子間の距離が一定以下になるときに衝突が必ず起こる場合
の断面積の解釈を表している。だが、実際の衝突では、必ずしも粒子
回の衝突が
起きることになって式(8.6.341)に一致する。この例は、剛体球どう
しの衝突のように粒子間の距離が一定以下になるときに衝突が必ず起こる場合
の断面積の解釈を表している。だが、実際の衝突では、必ずしも粒子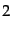 の近
くに来た粒子がすべて散乱するわけではないのでこの簡単な解釈をそのまま受
け止めてはいけないが、いずれにしても断面積は衝突の確率を表すものであり、
面積の次元をもつ量である。
の近
くに来た粒子がすべて散乱するわけではないのでこの簡単な解釈をそのまま受
け止めてはいけないが、いずれにしても断面積は衝突の確率を表すものであり、
面積の次元をもつ量である。
ここで、相対速度はそのままではローレンツ系に依存する概念であって、この
ままでは断面積のローレンツ不変性が明らかではない。そこで、ローレンツ不
変な断面積の定義を得るには、相対速度
 を任意のローレンツ系
であいまいさなく定義する必要がある。断面積の定義式(8.6.341),
(8.6.342)に現れてくる
を任意のローレンツ系
であいまいさなく定義する必要がある。断面積の定義式(8.6.341),
(8.6.342)に現れてくる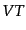 は明らかにローレンツ不変である。また、
粒子の静止系で数密度
は明らかにローレンツ不変である。また、
粒子の静止系で数密度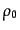 をもつ粒子群が速度
をもつ粒子群が速度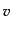 で動く場合、体積のロー
レンツ変換から、数密度は
で動く場合、体積のロー
レンツ変換から、数密度は
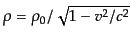 で与えられる。
さらに、この粒子のエネルギーは
で与えられる。
さらに、この粒子のエネルギーは
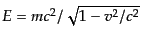 であるから、
であるから、
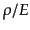 はローレンツ不変である。したがって、積
はローレンツ不変である。したがって、積
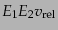 が
不変量になるように相対速度を定義すれば断面積も不変量になることがわかる。
そこで、この条件を満たす相対速度として、粒子の4 元運動量
が
不変量になるように相対速度を定義すれば断面積も不変量になることがわかる。
そこで、この条件を満たす相対速度として、粒子の4 元運動量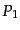 ,
, 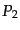 を
用いて
を
用いて
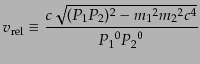 |
(H.6.343) |
のように定義する。どちらかの粒子が静止している実験室系、あるいは粒子の
重心系など、粒子 ,
, 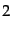 の速度
の速度
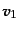 ,
,
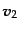 が平行になるか、
あるいはどちらかの速度が0
になるような座標系においては、上の定義が本
来の相対速度
が平行になるか、
あるいはどちらかの速度が0
になるような座標系においては、上の定義が本
来の相対速度
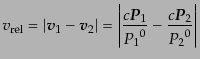 |
(H.6.344) |
を表していることは容易に確かめられる。ここで質量がゼロの極限をとること
ができるので、質量のない粒子の場合もこの定義を用いることができる。
さて、粒子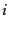 の運動量を
の運動量を
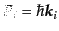 , またその他粒子の
種類、スピンや偏極などを表す添字をまとめて簡略に
, またその他粒子の
種類、スピンや偏極などを表す添字をまとめて簡略に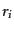 と表すことにする。
このとき一般に生成消滅演算子は
と表すことにする。
このとき一般に生成消滅演算子は
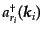 ,
,
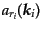 と書かれる。これら運動量が離散化されていない生成消
滅演算子により作られる粒子状態
と書かれる。これら運動量が離散化されていない生成消
滅演算子により作られる粒子状態
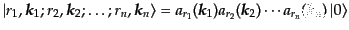 |
(H.6.345) |
はノルムは1ではない。例えば一粒子状態では、
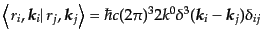 |
(H.6.346) |
などとなり、右辺はローレンツ不変である。このような規格化のことを不変規格化(invariant normalization)と呼ぶ。この不変規格化のもとで、始
状態を
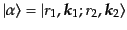 、終状態を
、終状態を
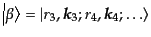 とする。ここで、
始状態のノルムは
とする。ここで、
始状態のノルムは
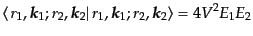 |
(H.6.347) |
となる。ただし、
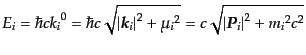 |
(H.6.348) |
は粒子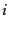 のエネルギーである。したがって、この始状態は粒子1, 2がそれぞ
れ単位体積あたり
のエネルギーである。したがって、この始状態は粒子1, 2がそれぞ
れ単位体積あたり
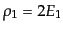 および
および
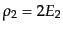 ずつ一様に分布して
いる状態に対応する。
ずつ一様に分布して
いる状態に対応する。
S行列演算子の性質(8.6.311)から、始状態
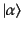 は反応後に
は
は反応後に
は
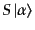 という状態になっている。そこでこの状態を運動量以外の
状態
という状態になっている。そこでこの状態を運動量以外の
状態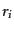 の確定した
の確定した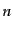 粒子状態で展開すれば、不変規格化をとっていること
を考慮して、
粒子状態で展開すれば、不変規格化をとっていること
を考慮して、
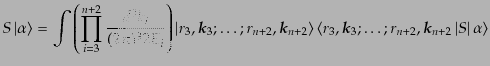 |
(H.6.349) |
となる。したがって、量子論の確率解釈に従えば、運動空間の体積素片
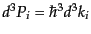 (
(
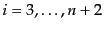 )の中に終状態
)の中に終状態
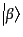 を見いだす確率は
を見いだす確率は
 |
(H.6.350) |
で与えられ、これは上で与えた不変規格化されたノルムを粒子数密度
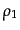 ,
, 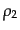 と解釈するときに、終状態がこの運動量範囲に散乱される
回数(8.6.342)を与えることになる。
と解釈するときに、終状態がこの運動量範囲に散乱される
回数(8.6.342)を与えることになる。
ここで散乱の前後では4元運動量が保存することから、
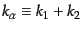 と
と
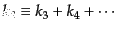 が等しくなければならず、こ
のため必ずS行列要素
が等しくなければならず、こ
のため必ずS行列要素
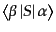 には
には
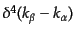 という因子が含まれる。そこで
という因子が含まれる。そこで
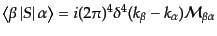 |
(H.6.351) |
と表すことができる。始状態
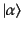 と終状態
と終状態
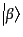 が不変規
格化されているとき、この
が不変規
格化されているとき、この
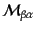 を不変散乱振幅
(invariant scattering amplitude)と呼ぶ。波数空間のデルタ関数のゼロ
点は有限体積化した時空間では
を不変散乱振幅
(invariant scattering amplitude)と呼ぶ。波数空間のデルタ関数のゼロ
点は有限体積化した時空間では
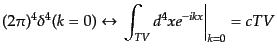 |
(H.6.352) |
と表されるから、式(8.6.350)は
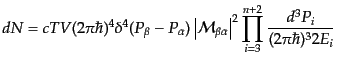 |
(H.6.353) |
となる。したがって、式(8.6.342)の微分散乱断面積は、
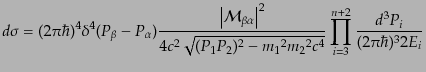 |
(H.6.354) |
と表されることがわかり、S行列要素を得れば求められることになる。また、
全断面積はこの式をすべての終状態の運動量で積分することにより得られる。
ここで、全断面積の積分においては、終状態に同種粒子が含まれる場合、その
まま積分すると同じ状態を多重に積分してしまうことになる。そこで、粒子
 のなかに同種粒子が
のなかに同種粒子が
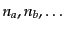 個ずつ含まれるときに
は、対称性の因子
個ずつ含まれるときに
は、対称性の因子
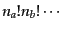 で割る必要がある。
で割る必要がある。
終状態も2粒子状態となる2体反応については、重心系で記述することによりさ
らに簡略化した式で表される。まず、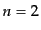 とした式(8.6.354)におい
て、
とした式(8.6.354)におい
て、 を実行してしまえば、運動量の3次元デルタ関数の部分が消える.
ただしここで,
を実行してしまえば、運動量の3次元デルタ関数の部分が消える.
ただしここで,
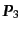 は運動量保存を満たすように他の変数で置き換え
られたものと理解する.すると,重心系においては
は運動量保存を満たすように他の変数で置き換え
られたものと理解する.すると,重心系においては
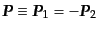 ,
,
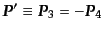 と
おくことができ、このとき
と
おくことができ、このとき
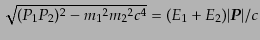 となり、微分断面積は
となり、微分断面積は
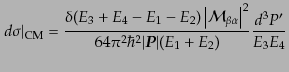 |
(H.6.355) |
と表される。ここで、
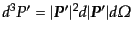 と極座標
で表示する。デルタ関数の中の
と極座標
で表示する。デルタ関数の中の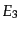 ,
, 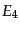 は
は
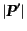 の関数となってい
るので、このままでは積分が自明でない.そこで,
の関数となってい
るので、このままでは積分が自明でない.そこで,
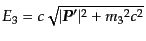 ,
,
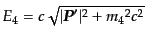 であるから、
であるから、
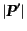 を
を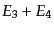 に変数変換すると、
に変数変換すると、
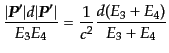 |
(H.6.356) |
となる。これにより
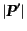 についての積分も実行してしまえば、結局微
分断面積の重心系での表式は
についての積分も実行してしまえば、結局微
分断面積の重心系での表式は
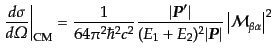 |
(H.6.357) |
となる。ただし、この表式で
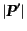 は次式で与えられる:
は次式で与えられる:
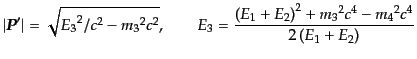 |
(H.6.358) |
次に、初期状態が一粒子状態であるような反応:
 |
(H.6.359) |
を考える。この場合はこの粒子1が不安定であって時間の経過とともにより軽
い粒子群に崩壊する現象を表すことになる。このような反応の起る確率を表す
量として、崩壊幅と呼ばれるものが用いられるので、以下にこれを与える。ま
ず、不変規格化された初期状態
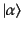 から出発して、終状態
から出発して、終状態
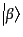 が運動量空間の体積要素
が運動量空間の体積要素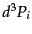 (
(
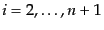 )に見
いだされる回数は断面積の場合の式(8.6.353)と同様の式
)に見
いだされる回数は断面積の場合の式(8.6.353)と同様の式
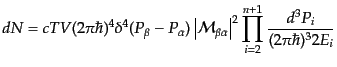 |
(H.6.360) |
で与えられる。ここで、崩壊する粒子の静止系で考えると、
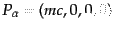 である。始状態は全空間に
である。始状態は全空間に
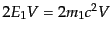 個の粒子が存在
する不変規格化であったから、単位時間あたりにこの運動量体積素片に崩壊す
る確率は、
個の粒子が存在
する不変規格化であったから、単位時間あたりにこの運動量体積素片に崩壊す
る確率は、
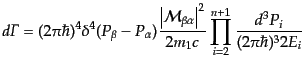 |
(H.6.361) |
で与えられ、この量は微分崩壊幅 (differential decay width)と呼ば
れる。ある粒子群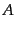 へ崩壊する終状態のすべての運動量について積分した量
へ崩壊する終状態のすべての運動量について積分した量
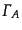 は、この粒子群へ崩壊する確率を表し、これをチャネル
は、この粒子群へ崩壊する確率を表し、これをチャネル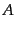 への
部分崩壊幅 (partial decay width)と呼ぶ。この場合にも、終状態に同
種粒子が含まれている場合には、適切な対称性因子
への
部分崩壊幅 (partial decay width)と呼ぶ。この場合にも、終状態に同
種粒子が含まれている場合には、適切な対称性因子
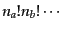 で割っ
ておく必要がある。可能なすべての粒子群への崩壊幅を足し上げたもの
で割っ
ておく必要がある。可能なすべての粒子群への崩壊幅を足し上げたもの
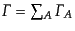 は、はじめの粒子が崩壊する全確率を表し、こ
れを全崩壊幅 (total decay width)と呼ぶ。全崩壊幅の逆数
は、はじめの粒子が崩壊する全確率を表し、こ
れを全崩壊幅 (total decay width)と呼ぶ。全崩壊幅の逆数
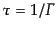 を崩壊する粒子の寿命 (life time)と呼ぶ。全崩壊幅に対す
る部分崩壊幅の割合
を崩壊する粒子の寿命 (life time)と呼ぶ。全崩壊幅に対す
る部分崩壊幅の割合
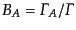 をチャネル
をチャネル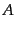 への分岐
比 (branching ratio)と呼ぶ。
への分岐
比 (branching ratio)と呼ぶ。
終状態が2粒子状態となる場合には、式(8.6.361)はより簡単な式で表
される。崩壊する粒子の静止系では、
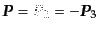 とおくことができるので、断面積の場合と同様にして、
とおくことができるので、断面積の場合と同様にして、
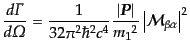 |
(H.6.362) |
と表される。ここで、
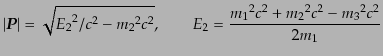 |
(H.6.363) |
である。
Footnotes
- ...
恒等式H8
- これは
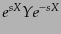 を
を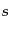 でテイラー展開すれば容易
に証明される。
でテイラー展開すれば容易
に証明される。
- ...としてやってH9
- この操作は数学的には多少乱
暴であるが、結果的にはこれでよい。ただし、厳密には、漸近場はハイゼンベ
ルグ場と演算子そのものとして漸近的に等しくなっているのではなく、くりこ
まれたハイゼンベルグ場と行列要素が漸近的に等しくなるという、弱い意味で
の同等性でなければならない。
- ...
こでは省略する.詳細は文献H10
- G. C. Wick, Phys. Rev. 80
268 (1950)
- ... H11
- 高野文彦 「多体問題」 (培風館,新物理学シリーズ
18, 1975)





次へ: 散乱断面積の計算例
上へ: 場の量子化と粒子の相互作用
前へ: 自由場の量子化
目次
索引
All rights reserved © T.Matsubara 2004-2010
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11
![]() が与えられたときに、
状態ベクトル
が与えられたときに、
状態ベクトル
![]() が時間発展し、その従う微分方程式は
シュレーディンガー方程式
が時間発展し、その従う微分方程式は
シュレーディンガー方程式
![]() の
時間発展によって表される。ここで、上添字のHはハイゼンベルグ描像を明示
するためにつけた。そのような演算子はすべて場の正準変数
の
時間発展によって表される。ここで、上添字のHはハイゼンベルグ描像を明示
するためにつけた。そのような演算子はすべて場の正準変数
![]() の関数であり、その満たす微分方程式はハイゼンベルグ方程式
の関数であり、その満たす微分方程式はハイゼンベルグ方程式
![]() として、そのときの状態ベクトルを
として、そのときの状態ベクトルを
![]() とする。すると、シュレーディンガー表示で
の時間発展の式(8.6.272)の解は形式的に、
とする。すると、シュレーディンガー表示で
の時間発展の式(8.6.272)の解は形式的に、
![]() 粒子状態が時間発展し、
粒子状態が時間発展し、
![]() 、および十分以後
、および十分以後
![]() では相互作用のない、自由
な状態になっているので、場は自由ハイゼンベルグ演算子となっているであろ
う。この仮定は漸近条件と呼ばれる。ただし、ここではより厳密な議論を避け、
直観的な説明をすることにする。衝突の十分以前の自由ハイゼンベルグ演算子
では相互作用のない、自由
な状態になっているので、場は自由ハイゼンベルグ演算子となっているであろ
う。この仮定は漸近条件と呼ばれる。ただし、ここではより厳密な議論を避け、
直観的な説明をすることにする。衝突の十分以前の自由ハイゼンベルグ演算子
![]() の生成消滅演算子を
の生成消滅演算子を
![]() ,
,
![]() とし、また、衝突の十分以後の自由ハイゼンベルグ演
算子
とし、また、衝突の十分以後の自由ハイゼンベルグ演
算子
![]() の生成消滅演算子を
の生成消滅演算子を
![]() ,
,
![]() とする。すると、それぞれのフォッ
ク基底は
とする。すると、それぞれのフォッ
ク基底は
![]() から、
out状態の生成演算子を用いて構成される状態
から、
out状態の生成演算子を用いて構成される状態
![]() へと相
互作用の結果変化する過程を考え、次の量
へと相
互作用の結果変化する過程を考え、次の量
![]() を基準
としたときの時刻
を基準
としたときの時刻![]() の状態ベクトルの形を求めてみると、相互作用表示の状
態ベクトルの時間発展の式(8.6.288) により、
の状態ベクトルの形を求めてみると、相互作用表示の状
態ベクトルの時間発展の式(8.6.288) により、
![]() から
から![]() まで積分すると、
まで積分すると、
![]() ,
,
![]() をとれば式(8.6.309)よりS行列を与える
ことがわかり、
をとれば式(8.6.309)よりS行列を与える
ことがわかり、
![]() が場の微分を含まない,
すなわち相互作用が微分結合を含まない場合,共役変数
が場の微分を含まない,
すなわち相互作用が微分結合を含まない場合,共役変数
![]() は相互作用項に無関係に決まるから,
は相互作用項に無関係に決まるから,
![]() により求められる相互作用ハミルトニアン
密度は
により求められる相互作用ハミルトニアン
密度は
![]() となる.したがって,この
ダイソンの公式はこの場合,
となる.したがって,この
ダイソンの公式はこの場合,
![]() について、
について、
![]() にしか依存し
ない。また、真空期待値で挟んでいることから、必ず生成演算子と消滅演算子
がペアで含まれなければならないので、スピノル場とベクトル場など、異なる
種類の場の縮約はゼロになる。そこで、ゼロでない縮約は実スカラー場、複素
スカラー場、ディラック場、実ベクトル場のそれぞれの場合に次のように書け
ることになる:
にしか依存し
ない。また、真空期待値で挟んでいることから、必ず生成演算子と消滅演算子
がペアで含まれなければならないので、スピノル場とベクトル場など、異なる
種類の場の縮約はゼロになる。そこで、ゼロでない縮約は実スカラー場、複素
スカラー場、ディラック場、実ベクトル場のそれぞれの場合に次のように書け
ることになる:
![]() を用いて、
を用いて、
![]() が衝突して、粒子
が衝突して、粒子
![]() となるような散
乱過程
となるような散
乱過程
![]() の静止系で考えて
みる。図8.2のように、粒子
の静止系で考えて
みる。図8.2のように、粒子![]() に向かって多数の粒子
に向かって多数の粒子![]() が相対速度
が相対速度
![]() で向かってくる。
で向かってくる。
![]() を任意のローレンツ系
であいまいさなく定義する必要がある。断面積の定義式(8.6.341),
(8.6.342)に現れてくる
を任意のローレンツ系
であいまいさなく定義する必要がある。断面積の定義式(8.6.341),
(8.6.342)に現れてくる![]() は明らかにローレンツ不変である。また、
粒子の静止系で数密度
は明らかにローレンツ不変である。また、
粒子の静止系で数密度![]() をもつ粒子群が速度
をもつ粒子群が速度![]() で動く場合、体積のロー
レンツ変換から、数密度は
で動く場合、体積のロー
レンツ変換から、数密度は
![]() で与えられる。
さらに、この粒子のエネルギーは
で与えられる。
さらに、この粒子のエネルギーは
![]() であるから、
であるから、
![]() はローレンツ不変である。したがって、積
はローレンツ不変である。したがって、積
![]() が
不変量になるように相対速度を定義すれば断面積も不変量になることがわかる。
そこで、この条件を満たす相対速度として、粒子の4 元運動量
が
不変量になるように相対速度を定義すれば断面積も不変量になることがわかる。
そこで、この条件を満たす相対速度として、粒子の4 元運動量![]() ,
, ![]() を
用いて
を
用いて
![]() の運動量を
の運動量を
![]() , またその他粒子の
種類、スピンや偏極などを表す添字をまとめて簡略に
, またその他粒子の
種類、スピンや偏極などを表す添字をまとめて簡略に![]() と表すことにする。
このとき一般に生成消滅演算子は
と表すことにする。
このとき一般に生成消滅演算子は
![]() ,
,
![]() と書かれる。これら運動量が離散化されていない生成消
滅演算子により作られる粒子状態
と書かれる。これら運動量が離散化されていない生成消
滅演算子により作られる粒子状態
![]() は反応後に
は
は反応後に
は
![]() という状態になっている。そこでこの状態を運動量以外の
状態
という状態になっている。そこでこの状態を運動量以外の
状態![]() の確定した
の確定した![]() 粒子状態で展開すれば、不変規格化をとっていること
を考慮して、
粒子状態で展開すれば、不変規格化をとっていること
を考慮して、
![]() と
と
![]() が等しくなければならず、こ
のため必ずS行列要素
が等しくなければならず、こ
のため必ずS行列要素
![]() には
には
![]() という因子が含まれる。そこで
という因子が含まれる。そこで
![]() とした式(8.6.354)におい
て、
とした式(8.6.354)におい
て、![]() を実行してしまえば、運動量の3次元デルタ関数の部分が消える.
ただしここで,
を実行してしまえば、運動量の3次元デルタ関数の部分が消える.
ただしここで,
![]() は運動量保存を満たすように他の変数で置き換え
られたものと理解する.すると,重心系においては
は運動量保存を満たすように他の変数で置き換え
られたものと理解する.すると,重心系においては
![]() ,
,
![]() と
おくことができ、このとき
と
おくことができ、このとき
![]() となり、微分断面積は
となり、微分断面積は
![]() とおくことができるので、断面積の場合と同様にして、
とおくことができるので、断面積の場合と同様にして、
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11