




次へ: 相対論的運動学
上へ: 場の量子化と粒子の相互作用
前へ: 量子場の相互作用
目次
索引
Subsections
散乱断面積の具体的な計算例として、はじめに固定したクーロンポテンシャル
中での電子の散乱,すなわちラザフォード散乱を考える.この系のラグランジ
アン密度は単位電荷を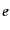 とするとき,式(8.4.189)で
とするとき,式(8.4.189)で とおい
たもので与えられ,電子と光子の相互作用部分は正規積の規約を考慮に入れて,
とおい
たもので与えられ,電子と光子の相互作用部分は正規積の規約を考慮に入れて,
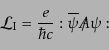 |
(H.7.364) |
となる.いま,クーロンポテンシャル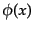 は固定された電荷
は固定された電荷 に
より与えられ,ベクトルポテンシャルはゼロであるから,光子の場は
に
より与えられ,ベクトルポテンシャルはゼロであるから,光子の場は
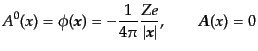 |
(H.7.365) |
という静的な古典場として与えられる.この場合クーロンポテンシャルの静止
系で考えていることになる.したがってこのとき相互作用ラグランジアンは
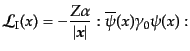 |
(H.7.366) |
で与えられることになる.ここで,
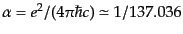 は微細構造定数とよばれる無次元量であるH12.
は微細構造定数とよばれる無次元量であるH12.
まず,いま考えている系で散乱断面積とS行列の関係を求めておく.ある十分
長い時間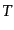 において,数密度
において,数密度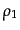 , 速度
, 速度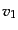 をもつ電子のビームがある
運動量体積素片
をもつ電子のビームがある
運動量体積素片 の終状態へ散乱される回数を
の終状態へ散乱される回数を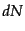 とするとき,この
終状態への微分散乱断面積
とするとき,この
終状態への微分散乱断面積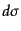 は
は
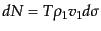 |
(H.7.367) |
により与えられる(図8.2をみよ).いま,
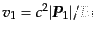 であり,また不変規格化のもとでは
であり,また不変規格化のもとでは
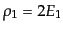 と対
応する.また
と対
応する.また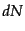 はは式(8.6.350)に類似の
はは式(8.6.350)に類似の
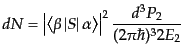 |
(H.7.368) |
で与えられるから,微分断面積は
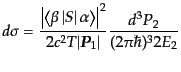 |
(H.7.369) |
となる.いま,クーロン場が固定されているため,電子の運動量は散乱の前後
で保存しないが,エネルギーは保存する.このため,このあと具体的にも示さ
れるが,必ずS行列要素には
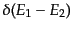 の因子が含まれる.そこで,
の因子が含まれる.そこで,
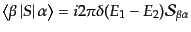 |
(H.7.370) |
とおける.これを2乗したときに出てくるデルタ関数の2乗の部分は式
(8.6.352)と同じ考え方で,
| |
|
![$\displaystyle \left[2\pi \delta(E_1 - E_2)\right]^2 =
2\pi \delta(E_1 - E_2)\c...
...\hbar}\int dt e^{i(E_1 - E_2)t/\hbar} =
\frac{2\pi T}{\hbar} \delta(E_1 - E_2)$](img2210.png) |
(H.7.371) |
となる.また,終状態の運動量微小体積素片は極座標で
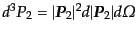 とかかれ,
とかかれ,
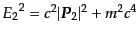 により
により
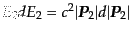 で
あることを用いると,
で
あることを用いると,
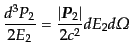 |
(H.7.372) |
となる.したがって微分断面積は
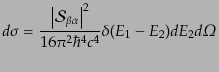 |
(H.7.373) |
となる.ここで,エネルギーの保存を表すデルタ関数のため
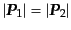 となることを用いた.ここでデルタ関数の存在はエネルギー保
存を満たさない終状態には粒子が散乱されないことをあらわに示していて,
となることを用いた.ここでデルタ関数の存在はエネルギー保
存を満たさない終状態には粒子が散乱されないことをあらわに示していて,
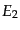 の範囲を終状態に指定することは適切でないことを示している.したがっ
て
の範囲を終状態に指定することは適切でないことを示している.したがっ
て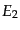 で積分することにより,微分断面積は
で積分することにより,微分断面積は
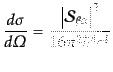 |
(H.7.374) |
で表されることになる.
S行列要素
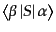 はダイソンの公式
(8.6.317)を展開して計算する.
はダイソンの公式
(8.6.317)を展開して計算する.
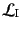 に関して展開
した摂動の
に関して展開
した摂動の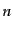 次の項を
次の項を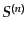 と表記すると,
と表記すると,
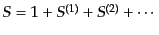 とかく.いま摂動の0次の項は相互作用がない場合と同じで全く散乱
されない状況を表すので,
とかく.いま摂動の0次の項は相互作用がない場合と同じで全く散乱
されない状況を表すので,
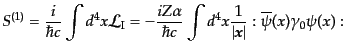 |
(H.7.375) |
が散乱に関する摂動の最低次の近似を与える.この積分はひとつの時空点しか
含んでいないので,T積をつける必要はない.入射する電子の運動量を
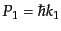 , スピンを
, スピンを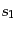 とし,散乱される電子のものをそれぞれ
とし,散乱される電子のものをそれぞれ
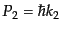 ,
, 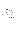 とすると,始状態と終状態はそれぞれ
とすると,始状態と終状態はそれぞれ
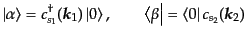 |
(H.7.376) |
で与えられる.ここで,式(8.5.246), (8.5.247)で与えられ
るスピノル場の平面波展開,すなわち
を式(8.7.375)に代入した場合,反電子の生成消滅演算子
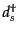 ,
, 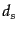 を含む項は行列要素
を含む項は行列要素
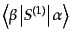 を計算するときに直接
を計算するときに直接
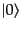 や
や
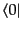 にかかることになって消えてしまい,寄与することはない.
したがってS行列要素の1次の項は
にかかることになって消えてしまい,寄与することはない.
したがってS行列要素の1次の項は
| |
|
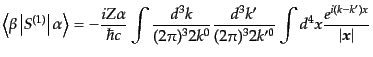 |
|
| |
|
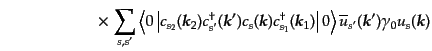 |
(H.7.379) |
となる.ここで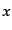 の積分はラプラシアンのグリーン関数の関係
の積分はラプラシアンのグリーン関数の関係
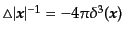 を使えば部分積分により,
を使えば部分積分により,
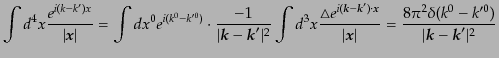 |
(H.7.380) |
と計算できる.さらに生成消滅演算子の積の真空期待値の部分は反交換関係
(8.5.248)を前の二つのペアと後ろの二つのペアに用いることで,
| |
|
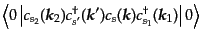 |
|
| |
|
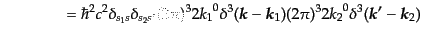 |
(H.7.381) |
となる.こうして1次のS行列要素は次の形となる:
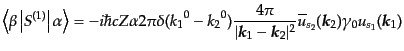 |
(H.7.382) |
あるいは式(8.7.370)の記法では,
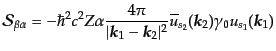 |
(H.7.383) |
となるので,微分散乱断面積(8.7.374)は
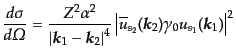 |
(H.7.384) |
で与えられる.ここで,
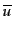 の定義
の定義
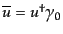 , および
, および
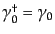 を用いれば,最後の因子は
を用いれば,最後の因子は
と書き換えられる.ここで,形
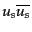 は式(8.4.166)の
は式(8.4.166)の
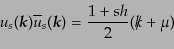 |
(H.7.386) |
に置き換えられる.射影行列 は式(8.4.162)のように
は式(8.4.162)のように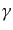 行列で
表すことができるから,結局上の式のトレースの中の行列はすべて
行列で
表すことができるから,結局上の式のトレースの中の行列はすべて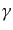 行
列となって,それを計算すれば散乱断面積の計算が終わることになる.
行
列となって,それを計算すれば散乱断面積の計算が終わることになる.
だが,多くの場合には入射電子と散乱電子の偏極の自由度は測られないなど,
無視して取り扱ってよいことが多く,このときにはトレースの計算が簡単にな
る.ここからはそのような場合を考えることにする.入射電子はどの偏極も同
じ確率であるから,散乱断面積の計算において,始状態のスピン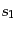 につい
ては平均をとる.また,散乱電子の偏極は測られないので,終状態のスピン
につい
ては平均をとる.また,散乱電子の偏極は測られないので,終状態のスピン
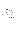 については和をとることになる.したがって偏極なしの微分散乱断面積
は
については和をとることになる.したがって偏極なしの微分散乱断面積
は
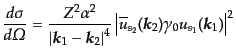 |
(H.7.387) |
で与えられることになる.ここで,式(8.7.385)を用いてからスピン和
をとると,式(8.4.167),すなわち
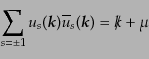 |
(H.7.388) |
を用いて簡単化されることになる.つまり,次のように変形される:
![\begin{equation*}\sum_{s_1, s_2} \left\vert \overline{u}_{s_2}({\mbox{\boldmath$...
...\gamma_0 (\ooalign{\hfil/\hfil\crcr$k$}_1 + \mu) \gamma_0 \right]\end{equation*}](img2250.png) |
(H.7.389) |
ここで,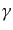 行列に関するトレースの公式
行列に関するトレースの公式
| |
|
![$\displaystyle {\rm Tr}\left[\gamma_\mu \gamma_\nu\right] = -4\eta_{\mu\nu},$](img2251.png) |
(H.7.390) |
| |
|
![$\displaystyle {\rm Tr}\left[(\mbox{奇数個の$\gamma$行列の積})\right] = 0,$](img2252.png) |
(H.7.391) |
| |
|
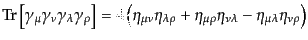 |
(H.7.392) |
を用いれば上の式が計算でき,
| |
|
![$\displaystyle \sum_{s_1, s_2}
\left\vert
\overline{u}_{s_2}({\mbox{\boldmath$...
...[{\gamma_0}^2\right] =
4\left( 2 {k_1}^0 {k_2}^0 + k_1\cdot k_2 + \mu^2\right)$](img2254.png) |
|
| |
|
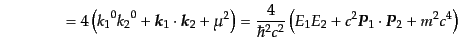 |
(H.7.393) |
となる.ここでエネルギー保存から散乱前後で電子のエネルギーと運動量の絶
対値は等しいので,それを
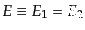 ,
,
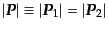 とおく.4元速度の絶対値も散乱前後で等しく,
それを,
とおく.4元速度の絶対値も散乱前後で等しく,
それを,
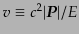 とおく.このとき,散乱角を
とおく.このとき,散乱角を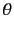 と
すると,
と
すると,
| |
|
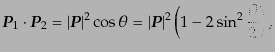 |
(H.7.394) |
| |
|
 |
(H.7.395) |
となるから,式(8.7.387)に式(8.7.393)を入れて計算すること
により,散乱断面積の最終的結果
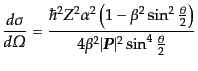 |
(H.7.396) |
を得る.ただしここで,
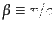 である.この散乱断面積の式は
モット散乱公式(Mott scattering formula)として知られるものである.
非相対論の極限
である.この散乱断面積の式は
モット散乱公式(Mott scattering formula)として知られるものである.
非相対論の極限
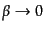 をとると,ラザフォードの散乱公
式 (Rutherford's scattering formula)
をとると,ラザフォードの散乱公
式 (Rutherford's scattering formula)
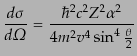 |
(H.7.397) |
に帰着する.
次に2つの電子が衝突して再び2つの電子となって散乱されるプロセス,すな
わち電子・電子散乱を考える.この散乱はメラー散乱 (Møller
scattering)と呼ばれる.相互作用ラグランジアン密度は同じで,式
(8.7.364)で与えられ,散乱断面積は式(8.6.354)で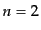 とし
たもの,また重心系では式(8.6.358)で与えられる.始状態
とし
たもの,また重心系では式(8.6.358)で与えられる.始状態
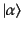 と終状態
と終状態
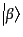 は
は
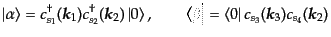 |
(H.7.398) |
で与えられる.このとき,S行列要素の計算において,一次の摂動 は
寄与しない.これは
は
寄与しない.これは が光子場
が光子場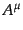 をひとつしか含まないため,そ
の中の生成消滅演算子が
をひとつしか含まないため,そ
の中の生成消滅演算子が
 か
か
 にかかって消えてしまうからで
ある.したがって,消えることのない摂動の最低次は
にかかって消えてしまうからで
ある.したがって,消えることのない摂動の最低次は
である.ここでT積に対しウィックの定理を適用して展開する.始めからある
正規順序積は縮約しないこと,また生成消滅演算子がペアで表れない縮約が消
えること,すなわち
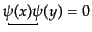 ,
,
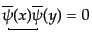 ,
,
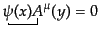 などを考慮して,
などを考慮して,
となる.ここで場の演算子を平面波展開して生成消滅演算子によって表し,式
(8.7.398)の始状態と終状態ではさめばS行列要素が計算される.
具体的な計算の前にまず,このようにS行列演算子をウィックの定理によって
展開したものからS行列要素を求めるための一般的な方針を説明しておく.ウィッ
クの定理により,S行列演算子は場の演算子の正規順序積の和で表現されてい
るので,消滅演算子がすべて右側に来ている.そこでS行列要素の計算におい
て,これらの消滅演算子を(反)交換関係を用いて始状態
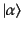 に含ま
れている生成演算子と交換し,どんどん右側へと移動させる.そして一番右に
その消滅演算子が来て
に含ま
れている生成演算子と交換し,どんどん右側へと移動させる.そして一番右に
その消滅演算子が来て
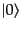 にかかって消えるまで続ける.このプロセス
において移動される消滅演算子は始状態の生成演算子のどれかひとつとペアを
つくって定数項を出し,それらがおつりの項として消えずに残ることになる.
ここでもし,始状態の生成演算子とペアをつくるのに十分な数の消滅演算子が
なければ,始状態の生成演算子のどれかはそのまま残されるが,それはS行列
演算子の中の生成演算子と反交換して終状態の消滅演算子のすぐ右側に到達す
る.ここで始状態にある粒子と同じ状態の粒子が終状態にあるとすると,それ
は散乱されなかったことを意味するから,散乱が起こったときの断面積を考え
る限り始状態の生成演算子は終状態の消滅演算子と反交換する.したがってS
行列を通り越してしまった始状態の生成演算子は
にかかって消えるまで続ける.このプロセス
において移動される消滅演算子は始状態の生成演算子のどれかひとつとペアを
つくって定数項を出し,それらがおつりの項として消えずに残ることになる.
ここでもし,始状態の生成演算子とペアをつくるのに十分な数の消滅演算子が
なければ,始状態の生成演算子のどれかはそのまま残されるが,それはS行列
演算子の中の生成演算子と反交換して終状態の消滅演算子のすぐ右側に到達す
る.ここで始状態にある粒子と同じ状態の粒子が終状態にあるとすると,それ
は散乱されなかったことを意味するから,散乱が起こったときの断面積を考え
る限り始状態の生成演算子は終状態の消滅演算子と反交換する.したがってS
行列を通り越してしまった始状態の生成演算子は
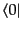 にかかって消えて
しまう.したがって,S行列演算子の右側に出てくる消滅演算子は必ず始状態
の粒子と同じ数だけなければならない(そうでなければ少なくともひとつの粒
子は散乱されない)ということになる.以上と同じことがS行列演算子の左側に
ある生成演算子についてもいえる.したがって,S行列演算子のウィックの定
理による展開においては,そこから出る生成消滅演算子がかならず始状態およ
び終状態の粒子とペアを作らなければならないことがわかる.
にかかって消えて
しまう.したがって,S行列演算子の右側に出てくる消滅演算子は必ず始状態
の粒子と同じ数だけなければならない(そうでなければ少なくともひとつの粒
子は散乱されない)ということになる.以上と同じことがS行列演算子の左側に
ある生成演算子についてもいえる.したがって,S行列演算子のウィックの定
理による展開においては,そこから出る生成消滅演算子がかならず始状態およ
び終状態の粒子とペアを作らなければならないことがわかる.
以上の考察のもと,具体的な式(8.7.400)を見てみると,散乱の起こる
S行列要素において残る項は電子の生成消滅演算子をそれぞれ2つずつ含む項
であるから,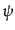 ,
,
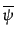 に関する縮約を全く含まない項と,
に関する縮約を全く含まない項と,
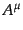 の縮約された項のみである.しかも,陽電子に関する項はすべて落ち
るから,
の縮約された項のみである.しかも,陽電子に関する項はすべて落ち
るから,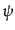 の正振動部分,
の正振動部分,
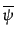 の負振動部分のみが生き残
る.したがって,
の負振動部分のみが生き残
る.したがって,
となる.ここで, の積分は
の積分は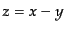 として積分することにより光子の
伝播関数のフーリエ変換(8.6.339)を用いて,
として積分することにより光子の
伝播関数のフーリエ変換(8.6.339)を用いて,
| |
|
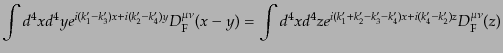 |
|
| |
|
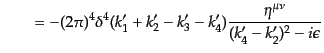 |
(H.7.402) |
となる.さらに真空期待値の部分は上に説明したように中の生成消滅演算子を
次々と左右に移動させていくことにより,
となる.こうして式(8.7.401)が計算できて,不変散乱振幅
(8.6.351)で書けば,
| |
|
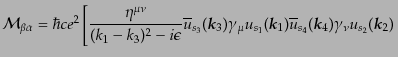 |
|
| |
|
![$\displaystyle \qquad\qquad\qquad\quad
\left. -
\frac{\eta^{\mu\nu}}{(k_1 - ...
...}({\mbox{\boldmath$k$}}_3) \gamma_\nu u_{s_2}({\mbox{\boldmath$k$}}_2)
\right]$](img2292.png) |
(H.7.404) |
となる.
ここで,断面積の計算のためには不変振幅の絶対値の2乗を計算する必要があ
る.ここで一般に任意の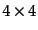 行列
行列
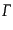 があるとき,
があるとき,
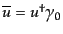 ,
,
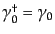 ,
,
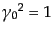 を用いると
を用いると
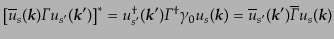 |
(H.7.405) |
となる.ただしここで,
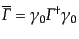 |
(H.7.406) |
である.とくに
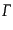 として
として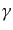 行列である場合,式
(8.4.132)-(8.4.134)と
行列である場合,式
(8.4.132)-(8.4.134)と
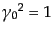 を使って,
を使って,
| |
|
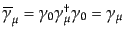 |
(H.7.407) |
| |
|
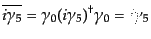 |
(H.7.408) |
| |
|
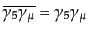 |
(H.7.409) |
となることが確かめられる.これらの関係を使って,不変振幅
(8.7.404)の絶対値2乗を計算していく.ここからは分母の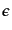 はここでゼロの極限をとってしまってもよく,以後は無視する.
はここでゼロの極限をとってしまってもよく,以後は無視する.
まず,括弧内の第一項について絶対値2乗を計算する.散乱において偏極を考
えないものとして,スピンについて和をとると,式(8.4.167)により,
となる.ここで
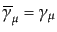 を用いている.第二項
の絶対値2乗は上の式において
を用いている.第二項
の絶対値2乗は上の式において
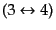 と入れ換えたもので与
えられる.他に第一項と第二項がクロスする項があるが,そのうち片方は以下
のようになる:
と入れ換えたもので与
えられる.他に第一項と第二項がクロスする項があるが,そのうち片方は以下
のようになる:
もう片方のクロス項は上式で
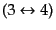 の置き換えをしたもの
で与えられる.
の置き換えをしたもの
で与えられる.
これらの式から,スピン和をとった不変散乱振幅の絶対値2乗を書き下せば
となる.
こうして、 行列のトレースの計算ができれば散乱断面積が求められる
ことになる.この目的のため,ここで有用なトレース計算の技術をまとめてお
く.まず,式(8.4.132)-(8.4.134)と
行列のトレースの計算ができれば散乱断面積が求められる
ことになる.この目的のため,ここで有用なトレース計算の技術をまとめてお
く.まず,式(8.4.132)-(8.4.134)と
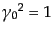 を
くり返し使って証明できる公式
を
くり返し使って証明できる公式
| |
|
![$\displaystyle {\rm Tr}\left[\gamma_\mu \gamma_\nu\right] = -4\eta_{\mu\nu},$](img2251.png) |
(H.7.413) |
| |
|
![$\displaystyle {\rm Tr}\left[(\mbox{奇数個の$\gamma$行列の積})\right] = 0,$](img2252.png) |
(H.7.414) |
| |
|
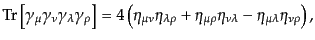 |
(H.7.415) |
| |
|
![$\displaystyle {\rm Tr}\left[\gamma_5\right] = 0,$](img2313.png) |
(H.7.416) |
| |
|
![$\displaystyle {\rm Tr}\left[\gamma_\mu \gamma_\nu \gamma_5\right] = 0,$](img2314.png) |
(H.7.417) |
| |
|
![$\displaystyle {\rm Tr}\left[\gamma_\mu \gamma_\nu \gamma_\lambda \gamma_\rho \gamma_5\right]
= -4i \epsilon_{\mu\nu\lambda\rho}$](img2315.png) |
(H.7.418) |
である.ここで,
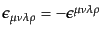 は
は
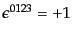 |
(H.7.419) |
で符合を定めた完全反対称テンソルである.完全反対称テンソルについては次
の双対則
| |
|
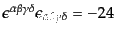 |
(H.7.420) |
| |
|
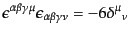 |
(H.7.421) |
| |
|
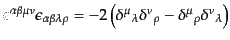 |
(H.7.422) |
が成り立つ.これら双対則は係数を除けば対称性から明らかで,係数はテンソ
ルの足について特別な場合を考えれば決められる.また,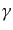 行列の順序
をトレースの中で逆転してももとの式に等しい,つまり,
行列の順序
をトレースの中で逆転してももとの式に等しい,つまり,
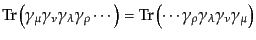 |
(H.7.423) |
である.この公式は式(8.4.136)の荷電共役行列
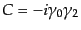 が
が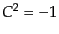 ,
,
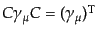 を満たす
ことを用いると証明できる.いま上の式で
を満たす
ことを用いると証明できる.いま上の式で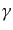 行列の数を
行列の数を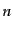 とすると
とすると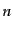 は偶数でなければ両辺ともにゼロであるから,偶数として証明すれば十分であ
る.すると
は偶数でなければ両辺ともにゼロであるから,偶数として証明すれば十分であ
る.すると
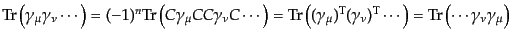 |
(H.7.424) |
と示される.
トレースの中で足が縮約している場合に便利なものは,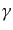 行列の反交換
関係(8.4.132)をくり返し使って得られる次の公式である:
行列の反交換
関係(8.4.132)をくり返し使って得られる次の公式である:
| |
|
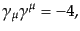 |
(H.7.425) |
| |
|
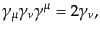 |
(H.7.426) |
| |
|
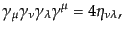 |
(H.7.427) |
| |
|
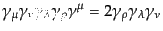 |
(H.7.428) |
| |
|
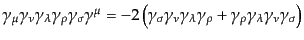 |
(H.7.429) |
また,同様に反交換関係を使って示される便利な関係式として,
| |
|
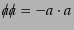 |
(H.7.430) |
| |
|
 |
(H.7.431) |
などがある.
これで不変散乱振幅のトレース計算に必要な準備が整った.あとはこれらの公
式を用いて計算していくだけである.トレースの中で足の縮約している
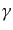 行列は縮約公式(8.7.425)-(8.7.429)を用いて行列
の数を減らし,あとはトレース公式(8.7.413)-(8.7.418)を
使ってトレースを計算していけばよい.例えば,行列のもっとも多い項として
式(8.7.412)のうち,8個の行列の積の計算は次のようになる:
行列は縮約公式(8.7.425)-(8.7.429)を用いて行列
の数を減らし,あとはトレース公式(8.7.413)-(8.7.418)を
使ってトレースを計算していけばよい.例えば,行列のもっとも多い項として
式(8.7.412)のうち,8個の行列の積の計算は次のようになる:
他の項も同様に計算する.ここで,入射,散乱する電子の波数ベクトルは
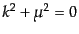 を満たし,さらにエネルギー運動量保存から
を満たし,さらにエネルギー運動量保存から
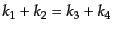 を満たすので,
を満たすので,
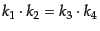 ,
,
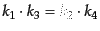 ,
,
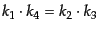 がそれぞれ成り立つ.これ
らの関係を使ってトレース計算の結果を整理すると,
がそれぞれ成り立つ.これ
らの関係を使ってトレース計算の結果を整理すると,
となる.ここから入射電子のスピンについて平均して散乱電子のスピンについ
て和をとった不変散乱振幅は
となる.
これを式(8.6.354)の
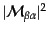 に置き換えれば
散乱断面積を一般的に得るが,いま2体反応なので重心系で記述することによ
り,より便利な式を得ることができる.重心系では
に置き換えれば
散乱断面積を一般的に得るが,いま2体反応なので重心系で記述することによ
り,より便利な式を得ることができる.重心系では
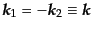 ,
,
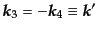 , また,
, また,
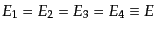 となる.したがって,重心系での2体反応の散
乱断面積の式(8.6.357)は
となる.したがって,重心系での2体反応の散
乱断面積の式(8.6.357)は
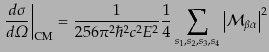 |
(H.7.436) |
となる.また,電子1と電子3の進む方向の間の角度を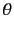 ,すなわち
,すなわち
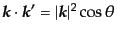 とすると,
とすると,
| |
|
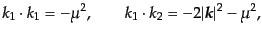 |
(H.7.437) |
| |
|
 |
(H.7.438) |
| |
|
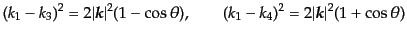 |
(H.7.439) |
となるから,これを式(8.7.435)へ入れて多少の三角関数の代数計算を
することにより,式(8.7.436)は
![$\displaystyle \left.\frac{d\sigma}{d{\mit\Omega}}\right\vert _{\rm CM} = \frac{...
... \frac{8E^4 - 4E^2 m^2 c^4 - m^4 c^8}{\sin^2\theta} + (E^2 - m^2 c^4)^2 \right]$](img2357.png) |
(H.7.440) |
という形になる.これが最終的なメラー散乱の微分断面積の表式である.
以上の計算において,S行列要素の計算の部分は,相互作用ラグランジアンか
ら作られるS行列演算子の摂動項をウィックの定理により可能な縮約の組合せ
へと分解し,縮約されずに残った正規順序積を始状態と終状態に含まれている
生成消滅演算子とペアにしていくという作業である.この作業は上のようにい
ちいち式変形で導くことなく,図形を考えることによって一度に終わらせてし
まうことのできる便利な方法がある.そこで用いられる図形はファイン
マン図形 (Feynman diagram)と呼ばれている.上の計算を振り返ってみると,
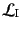 に含まれる演算子,あるいは始状態と終状態の生成消滅演
算子をペアにしていく作業であることがわかる.ここで,
に含まれる演算子,あるいは始状態と終状態の生成消滅演
算子をペアにしていく作業であることがわかる.ここで,
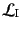 同士のペアからは伝播関数が発生し,
同士のペアからは伝播関数が発生し,
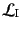 と始状態,終状態の
間のペアからは演算子の平面波展開の係数(上の場合
と始状態,終状態の
間のペアからは演算子の平面波展開の係数(上の場合
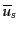 や
や
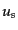 )が発生する.このことからまず,始状態や生成演算子が相互作用から出
る消滅演算子とペアをつくることに対して,始状態の粒子を図8.3で
表されるような外線に対応させる.
)が発生する.このことからまず,始状態や生成演算子が相互作用から出
る消滅演算子とペアをつくることに対して,始状態の粒子を図8.3で
表されるような外線に対応させる.
同様に終状態の粒子は図8.4で表されるような外線に対応させる.
これらの外線とペアをつくってつながる相互作用部
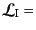 に
対応する図形として,図8.5で表されるような頂点を対応させる.
さらに,ウィックの定理における縮約を表す図形として,図8.6で表
されるような頂点と頂点を結ぶ内線を対応させる.
に
対応する図形として,図8.5で表されるような頂点を対応させる.
さらに,ウィックの定理における縮約を表す図形として,図8.6で表
されるような頂点と頂点を結ぶ内線を対応させる.
こうした対応関係のもと,外線を頂点で結び,頂点同士を内線で結ぶようなあ
らゆる場合を考えると,それらの図形がS行列要素の計算における展開の各項
に対応することになるのである.各図形の外線と内線は,S行列要素の計算に
おいて生成消滅演算子のペアが消えていることを表しているが,そのときに出
てくる因子は決まっていて,それらの因子が図に示してある.さらに頂点から
は相互作用ラグランジアンの係数が出てくる.こうして,ひとつの図形を書け
ば,その図形と因子の対応関係がわかってその図形がS行列要素へ寄与する項
の形が直ちに書き下せることになる.このように,ファインマン図形の部分と
それが寄与する因子の形の対応関係をファインマン則(Feynman rules)
という.図の外線と内線の因子を決めるのには,対応する波数を必要とする.
これは外線の場合には入射粒子と散乱粒子の運動量から決まる.また,頂点で
は入る運動量の和と出る運動量の和がゼロとなるようにする.これは頂点で伝
播関数の畳み込み積分が表れているため伝播関数
 が
つながっている頂点ではそのフーリエ変換
が
つながっている頂点ではそのフーリエ変換
 を使い,
を使い,
| |
|
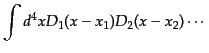 |
|
| |
|
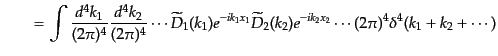 |
(H.7.441) |
などとなるからである.図形がループを含まない場合にはこれで内線の波数は
すべて決まるが,ループを含む場合,その決まらない波数 については積分
が残るので,積分
については積分
が残るので,積分
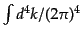 をする.このような規則により,図に
示した因子を用い,反応の順序に沿って頂点でスピノルの添字を縮約させ,全
体としてスカラーとなるように因子を掛け合わせれば不変散乱振幅に
をする.このような規則により,図に
示した因子を用い,反応の順序に沿って頂点でスピノルの添字を縮約させ,全
体としてスカラーとなるように因子を掛け合わせれば不変散乱振幅に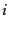 をか
けた
をか
けた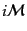 を求める規則になる.
を求める規則になる.
上で考えた過程のようにフェルミオンが関係する場合,演算子が反交換するの
で,符号について若干の注意が必要である.フェルミオン同士の演算子の交換
を奇数回含むような図形には,ファインマン規則によって得られた式にマイナ
ス符号が余計につく.図形の中でフェルミオンの線が交差するような場合,お
よびフェルミオンのループが存在する場合がそれにあたる.また,頂点と頂点,
頂点と外線を結ぶときに二通り以上のやり方がある場合はそれに応じた数をか
ける必要がある.このような点はわりあい間違いを犯しやすいので,常にウィッ
クの定理による計算を念頭におきながら,そのグラフがどのような計算で出て
くるのかを考えながらファインマン規則を適用することが大事である.
上で考えた電子・電子散乱の場合の最低次の摂動で可能なファインマン図は図
8.7の二つである.
図 8.7:
電子・電子散乱に対するファインマン図
|
|
このファインマン図からファインマン則によって不変散乱振幅を計算すると式
(8.7.404)となることを確かめるのは容易である.左の図は括弧内の第
一項に対応し,右の図は第二項に対応している.右の図ではフェルミオンの交
差を含むために逆符号になっている.ここでは摂動の最低次の近似をとってい
るからファインマン図の数は少なく,代数的な計算も比較的容易であったが,
摂動の次数を上げていけば飛躍的にファインマン図の数は増え,代数的な計算
によってS行列要素を得ることは非常に大変になる.この場合,ファインマン
則を用いることにより,圧倒的に計算を見通しよく進められることは容易に想
像できるだろう.
上の例では、フェルミオンと電磁場の共存系に関する場の量子論におけるラグ
ランジアンのファインマン則を与えた。このような系の量子論は量子電
磁力学 (Quantum Electrodynamics)と呼ばれ、場の量子論のプロトタイプと
なった理論である.その後弱い相互作用,強い相互作用についても同様に場の
量子論が適用できることが明らかになり,そのラグランジアンも知られている.
ここまでの計算から明らかなように,ファインマン則はラグランジアンが与え
られれば直ちに読み取ることができる.すなわち,ラグランジアンの運動項の
フーリエ変換の逆数によって内線に対応する伝播関数が与えられ,相互作用項
の係数から頂点に対応する因子が読み取れる.こうして,任意の(局所相互作
用のみを持つ)ラグランジアンが与えられれば,そこからファインマン則が読
み取れ,あとは可能なファインマン図を摂動の各次数ごとに求めて行くことに
より,任意の次数で反応の散乱断面積を求めることができるのである.場の量
子論において,摂動の最低次の計算はこのように比較的直線的である.摂動の
高次補正を求めようとすると,ファインマン図においてループを含む場合に発
散項が発生するため,くりこみという手続きが必要になる.その詳細について
は本章の目的を超えることになるのでここでは取り扱わないが,興味のある読
者はぜひ場の理論の専門書に進んで学んでいただきたい.
次に,電子と光子が散乱されるプロセスを考える.このプロセスはコン
プトン散乱(Compton scattering)と呼ばれる.ここでは演算子を用いた計算
を始めから行うことなく,上で導いたファインマン則の応用例としてファイン
マン図から不変散乱振幅を求めることからはじめる.このプロセスにおいて可
能なファインマン図は図8.8の2つである.
図 8.8:
コンプトン散乱に対するファインマン図
|
|
ここからファインマン則によって不変散乱振幅を求めると,
| |
|
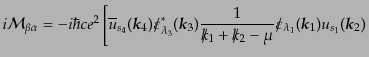 |
|
| |
|
![$\displaystyle \qquad\qquad\qquad\qquad
\left. + \
\overline{u}_{s_4}({\mbox{...
...lambda_3}^*({\mbox{\boldmath$k$}}_3)
u_{s_2}({\mbox{\boldmath$k$}}_2)
\right]$](img2373.png) |
(H.7.442) |
となる.ここで,括弧内第一項の電子の伝播関数の部分は
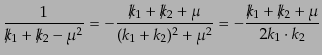 |
|
|
(H.7.443) |
となる.ここで,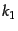 ,
, 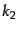 はそれぞれ入射光子と入射電子の4元運動量で
あるから
はそれぞれ入射光子と入射電子の4元運動量で
あるから
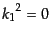 ,
,
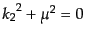 を満たすことを用いた.第二
項についても同様であり,不変散乱振幅は
を満たすことを用いた.第二
項についても同様であり,不変散乱振幅は
| |
|
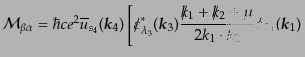 |
|
| |
|
![$\displaystyle \qquad\qquad\qquad\qquad\qquad
\left. -\
\ooalign{\hfil/\hfil\...
...lambda_3}^*({\mbox{\boldmath$k$}}_3)
\right]
u_{s_2}({\mbox{\boldmath$k$}}_2)$](img2380.png) |
(H.7.444) |
と書き直すことができる.
この散乱振幅を一般の座標系で計算するのはかなり面倒なので,始状態の電子
が静止している実験室系で考えることにする.この場合,入射光子の運動量の
向きに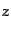 軸をとると
軸をとると
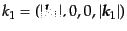 ,
,
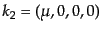 となる.この座標で偏極ベクトルとして式
(8.4.195)-(8.4.199)のようにとる.すると,偏極ベクトル
は実の量であり,また横偏極ベクトルは
となる.この座標で偏極ベクトルとして式
(8.4.195)-(8.4.199)のようにとる.すると,偏極ベクトル
は実の量であり,また横偏極ベクトルは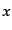 ,
, 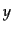 成分しか持たないから,入射
光子の横偏極ベクトルは入射粒子のどちらとも垂直になる:
成分しか持たないから,入射
光子の横偏極ベクトルは入射粒子のどちらとも垂直になる:
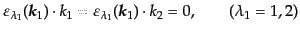 |
(H.7.445) |
始状態の電子は静止しているので,ゼロ成分を持たない横偏極ベクトルとは垂
直であり,さらに散乱光子の横偏極ベクトルも自分自身の波数ベクトルとは垂
直であるから次の式が成り立つ:
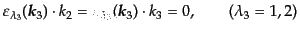 |
(H.7.446) |
入射光子,散乱光子ともに自由な実光子であるから横偏極成分しかなく,
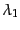 ,
, 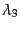 のとり得る値は
のとり得る値は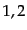 のみであるから,この座標系
では上の関係式は以下いつでも用いてよい.
のみであるから,この座標系
では上の関係式は以下いつでも用いてよい.
この座標系のもと,式(8.7.444)の括弧内第一項で分子の部分とそこか
ら右にかかっている因子の部分に着目する.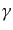 行
列の順序を反交換関係により交換して計算すると,
行
列の順序を反交換関係により交換して計算すると,
となる.ここで,最後の等式では式(8.7.445)および,ディラック方程
式(8.4.160)を用いた.同様に第二項についても
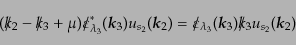 |
(H.7.448) |
となる.ここで実の偏極ベクトルを選んでいることを使った.こうして不変散
乱振幅(8.7.444)は次のように簡単化する:
![\begin{equation*}{\cal M}_{\beta\alpha} = - \hbar c e^2 \overline{u}_{s_4}({\mbo...
...$k$}_3}{2 k_2 \cdot k_3} \right] u_{s_1}({\mbox{\boldmath$k$}}_1)\end{equation*}](img2392.png) |
(H.7.449) |
この振幅の絶対値2乗について電子のスピンの和をとる.光子の偏極について
はいまはそのまま残しておくことにする.以下,繁雑になるので,
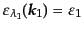 ,
,
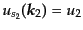 などのように略記する.計算の方針は
などのように略記する.計算の方針は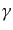 行
列の反交換関係(8.4.132)を用いて変形して
行
列の反交換関係(8.4.132)を用いて変形して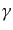 行列の数をなる
べく減らしていくことである.つまり,式(8.7.430),
(8.7.431)
行列の数をなる
べく減らしていくことである.つまり,式(8.7.430),
(8.7.431)
| |
|
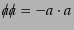 |
(H.7.450) |
| |
|
 |
(H.7.451) |
を使って変数を交換していく.
まず,第一項の絶対値2乗から出てくる因子として,
| |
|
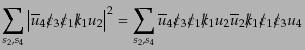 |
|
| |
|
![$\displaystyle \qquad =
{\rm Tr}\left[
\ooalign{\hfil/\hfil\crcr$\varepsilon$}...
...align{\hfil/\hfil\crcr$\varepsilon$}_3 \ooalign{\hfil/\hfil\crcr$k$}_4
\right]$](img2396.png) |
(H.7.452) |
と計算される.ここで,最後の等式では,
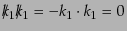 であること,さらに奇数個の
であること,さらに奇数個の 行列のトレースが消える
ことを用いた.さらに式(8.7.430), (8.7.431)を使って,
中の因子の次の部分の計算ができる:
行列のトレースが消える
ことを用いた.さらに式(8.7.430), (8.7.431)を使って,
中の因子の次の部分の計算ができる:
| |
|
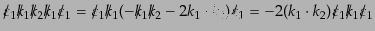 |
|
| |
|
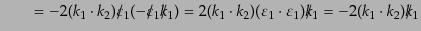 |
(H.7.453) |
ここで,3番目の等式では式(8.7.445)の
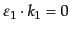 を用い,最後の等式では式(8.4.196), (8.4.197)から出
る
を用い,最後の等式では式(8.4.196), (8.4.197)から出
る
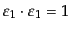 を用いている.したがって式
(8.7.452)は上式と式(8.7.415)を用いて
を用いている.したがって式
(8.7.452)は上式と式(8.7.415)を用いて
と計算できる.ここで式(8.7.446)とエネルギー運動量の保存から,
散乱光子の偏極ベクトルと散乱電子の運動量の内積は
 |
(H.7.455) |
となるので,
![\begin{equation*}\sum_{s_2, s_4} \left\vert \overline{u}_4 \ooalign{\hfil/\hfil\...
...ot k_2) \left[ 2(\varepsilon_3\cdot k_1)^2 - k_1\cdot k_4 \right]\end{equation*}](img2406.png) |
(H.7.456) |
が得られる.
同様に,式(8.7.449)の第二項の絶対値2乗を計算できるが,この項は
始めの項を
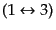 と置き換えたものなので,式
(8.7.454)まではこの置き換えによる式がそのまま成り立つ.
と置き換えたものなので,式
(8.7.454)まではこの置き換えによる式がそのまま成り立つ.
![\begin{equation*}\sum_{s_2, s_4} \left\vert \overline{u}_4 \ooalign{\hfil/\hfil\...
...t k_4) - (\varepsilon_1\cdot\varepsilon_1) (k_3\cdot k_4) \right]\end{equation*}](img2408.png) |
(H.7.457) |
散乱光子の偏極ベクトルと散乱電子の運動量の内積はこの場合には
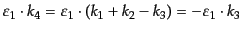 |
(H.7.458) |
となるので,
![\begin{equation*}\sum_{s_2, s_4} \left\vert \overline{u}_4 \ooalign{\hfil/\hfil\...
...ot k_3) \left[ 2(\varepsilon_1\cdot k_3)^2 + k_3\cdot k_4 \right]\end{equation*}](img2410.png) |
(H.7.459) |
が得られる.
次にクロス項の計算が必要である.必要な項は
である.この計算も同じようにして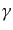 行列を反交換しながら数を減らし
ていけばよいが,より多くのステップが必要である.ここで,上の式で
行列を反交換しながら数を減らし
ていけばよいが,より多くのステップが必要である.ここで,上の式で
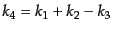 と置き換えると多少計算が簡単化する.あとは単調に計算す
ることにより,
と置き換えると多少計算が簡単化する.あとは単調に計算す
ることにより,
| |
|
![$\displaystyle \sum_{s_2, s_4}
\left[
\overline{u}_4
\ooalign{\hfil/\hfil\crc...
...fil/\hfil\crcr$\varepsilon$}_3
\ooalign{\hfil/\hfil\crcr$k$}_3
u_2
\right]^*$](img2415.png) |
|
| |
|
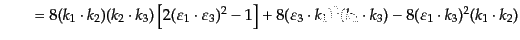 |
(H.7.461) |
という結果を得る.もう一方のクロス項は上式の複素共役で与えられるが,上
式は実であるから全く同じである.以上の結果を合わせることにより,
という結果を得る.ここで、始状態と終状態の4元運動量が質量殻上にあるこ
と、すなわち
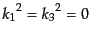 ,
,
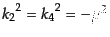 である
ことを使うと、関係
である
ことを使うと、関係
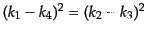 および
および
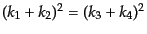 によりそれぞれ
によりそれぞれ
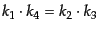 および
および
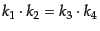 が従う。こうして結局
が従う。こうして結局
![$\displaystyle \sum_{s_2, s_4} \left\vert{\cal M}_{\beta\alpha}\right\vert^2 = 2...
...\cdot k_2}{k_2 \cdot k_3} + 4 (\varepsilon_1 \cdot \varepsilon_3)^2 - 2 \right]$](img2424.png) |
(H.7.463) |
となる。
さて,2体反応の散乱断面積の式(8.6.357)は便利な形をしているが,
重心系で導かれたものである.いま,実験室系において計算しているので,実
験室系での散乱断面積を不変散乱振幅を使って表す式が必要である.このため
には,式(8.6.357)を実験室系へローレンツ変換すればよい.実験室
系は重心系に対して重心系の入射電子の速度と同じ速度で動いている座標系で
ある.したがって対称性から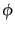 方向へはローレンツ変換を受けないので,
重心系と実験室系の散乱立体角をそれぞれ
方向へはローレンツ変換を受けないので,
重心系と実験室系の散乱立体角をそれぞれ
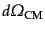 ,
,
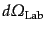 とすると,その変換のヤコビアンは
とすると,その変換のヤコビアンは
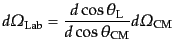 |
(H.7.464) |
である.ここで,
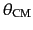 ,
,
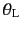 はそれぞれ重心系と
実験室系での散乱角である.したがってこの2つの系の間の角度
はそれぞれ重心系と
実験室系での散乱角である.したがってこの2つの系の間の角度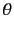 の変
換を求めればよいことになる.波数ベクトルの形は重心系において
の変
換を求めればよいことになる.波数ベクトルの形は重心系において
| |
|
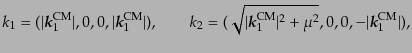 |
(H.7.465) |
| |
|
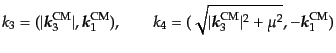 |
(H.7.466) |
また,実験室系において
| |
|
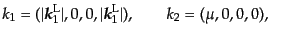 |
(H.7.467) |
| |
|
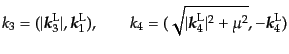 |
(H.7.468) |
と書ける.ここで,実験室系は重心系に対して、重心系の入射電子と同じ速度
で動いている.重心系での入射電子の速さは
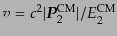 で与えられる.この速度を実験室系での波数ベクトルで表
すため,ローレンツ不変量
で与えられる.この速度を実験室系での波数ベクトルで表
すため,ローレンツ不変量
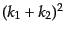 を両方の系で計算して等しいとお
くことにより,
を両方の系で計算して等しいとお
くことにより,
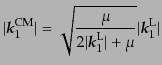 |
(H.7.469) |
を得る.したがって,実験室系は重心系に対して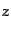 軸の負の方向へ速さ
軸の負の方向へ速さ
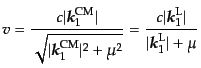 |
(H.7.470) |
で運動している.したがって散乱光子の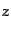 軸方向のローレンツ変換は
軸方向のローレンツ変換は
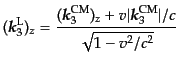 |
(H.7.471) |
で与えられ,これを極座標で書いて式(8.7.470)を代入すれば,
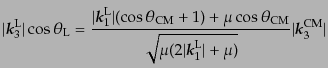 |
(H.7.472) |
となる.
ここで,重心系におけるエネルギー保存から,
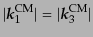 であることが従い,これと式(8.7.469)から,
であることが従い,これと式(8.7.469)から,
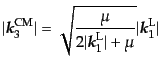 |
(H.7.473) |
であることがわかる.また,入射,散乱粒子が質量殻上にあることと関係
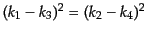 により,
により,
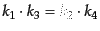 が従うが,この式へさらに
が従うが,この式へさらに
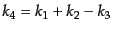 を代入して
を代入して
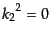 を使うと,
を使うと,
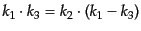 |
(H.7.474) |
を得る.この関係を実験室系の式(8.7.467), (8.7.468)を代
入することにより,
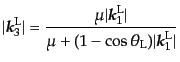 |
(H.7.475) |
を得る.これは実験室系において,入射光子と散乱光子の波数の関係,すなわ
ち振動数の関係をあたえるコンプトンの公式(Compton's formula)である.式
(8.7.473)と式(8.7.475)を式(8.7.472) へ代入する
ことにより,実験室系での入射光子の波数
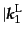 のみを用いて
のみを用いて
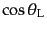 と
と
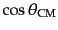 の関係が求まる.これを微分
することにより角度のヤコビアンが求まり,その結果
の関係が求まる.これを微分
することにより角度のヤコビアンが求まり,その結果
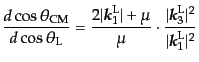 |
(H.7.476) |
となる.
重心系での入射粒子のエネルギーの和は次のようにローレンツ不変量を通じて
実験室系の量で表される:
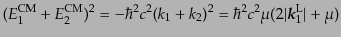 |
(H.7.477) |
また,重心系のエネルギー保存により
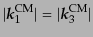 であったから,重心系の散乱断面積の公式
(8.6.357)は,いまの場合,
であったから,重心系の散乱断面積の公式
(8.6.357)は,いまの場合,
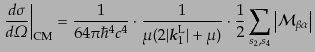 |
(H.7.478) |
ここで,電子のスピン状態を考えないものとして,入射電子のスピンについて
平均をとり,散乱電子のスピンについて和をとった.
また,不変散乱振幅の式(8.7.463)は実験室系の量
(8.7.467), (8.7.468)を用いて,
![$\displaystyle \sum_{s_2, s_4} \left\vert{\cal M}_{\beta\alpha}\right\vert^2 = 2...
...math$k$}}_3^{\rm L}\vert} + 4 (\varepsilon_1 \cdot \varepsilon_3)^2 - 2 \right]$](img2452.png) |
(H.7.479) |
と表される.したがって式(8.7.464), (8.7.476),
(8.7.478), (8.7.479)によって実験室系での散乱断面積の最
終的な表式
![$\displaystyle \left.\frac{d\sigma}{d{\mit\Omega}}\right\vert _{\rm Lab} = \frac...
...math$k$}}_3^{\rm L}\vert} + 4 (\varepsilon_1 \cdot \varepsilon_3)^2 - 2 \right]$](img2453.png) |
(H.7.480) |
を得る.あるいは,入射光子の振動数
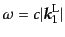 と光
子の進行方向に垂直方向を向いた3次元偏極ベクトル
と光
子の進行方向に垂直方向を向いた3次元偏極ベクトル
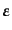 ,
とし,また散乱光子に対するそれらを
,
とし,また散乱光子に対するそれらを
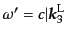 ,
,
 とすると,入射,散乱光子の偏極ベクトルは時間成分を
もたないから,
とすると,入射,散乱光子の偏極ベクトルは時間成分を
もたないから,
![$\displaystyle \left.\frac{d\sigma}{d{\mit\Omega}}\right\vert _{\rm Lab} = \frac...
...{\boldmath$\varepsilon$}} \cdot {\mbox{\boldmath$\varepsilon$}}')^2 - 2 \right]$](img2458.png) |
(H.7.481) |
とも表せる.この式はクライン・仁科の公式 (Klein-Nishina
formula)H13と呼ばれている.ここで,散乱光子の振動数は式(8.7.475)
すなわち,
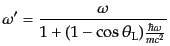 |
(H.7.482) |
を通じて入射光子の振動数と散乱角に関係している.ここで入射光子のエネル
ギーが電子の静止エネルギーに比べて小さい極限
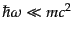 では,
では,
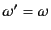 となって振動数の変化が無視できる.このときには散乱断
面積が
となって振動数の変化が無視できる.このときには散乱断
面積が
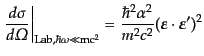 |
(H.7.483) |
となるが,これは古典電子による輻射の散乱を表すトムソン散乱公式
(Thomson's scattering formula)に一致する.トムソン散乱公式では,断面
積が光子のエネルギーに依らないが,量子効果が加わったクライン・仁科の公
式では,エネルギー依存するようになるという特徴がある.
最後に光子の偏極についても考えない場合,すなわち入射光子の偏極について
平均し,散乱光子の偏極について和をとった式を導いておく.偏極ベクトル
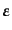 ,
,
 はそれぞれ
はそれぞれ
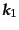 ,
,
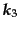 に垂直な単位ベクトルである.そこで入射光子の波数ベクトルに
より,式(8.4.197)-(8.4.199)のように作った完全系,
に垂直な単位ベクトルである.そこで入射光子の波数ベクトルに
より,式(8.4.197)-(8.4.199)のように作った完全系,
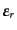 (
(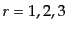 )および,散乱光子の波数ベクトルにより
作った
)および,散乱光子の波数ベクトルにより
作った
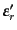 (
(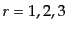 )を導入する.どちらも完全系をな
すので,
)を導入する.どちらも完全系をな
すので,
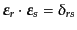 ,
,
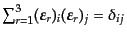 および,プライムのついた同様の式が成り立つ.このことを用い
ると,偏極ベクトルの部分は次のように計算できる:
および,プライムのついた同様の式が成り立つ.このことを用い
ると,偏極ベクトルの部分は次のように計算できる:
これを式(8.7.481)において入射光子の偏極ベクトルの平均,および
散乱光子の偏極ベクトルの和をとったものに用いれば,偏極ベクトルの部分は
上式の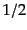 倍に置き換わり,他の部分は単に2倍されるから,
倍に置き換わり,他の部分は単に2倍されるから,
![$\displaystyle \left.\frac{d\sigma}{d{\mit\Omega}}\right\vert _{\rm Lab} = \frac...
... \frac{\omega'}{\omega} + \frac{\omega}{\omega'} - \sin^2\theta_{\rm L} \right]$](img2476.png) |
(H.7.485) |
となる.この式でも古典極限
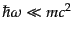 をとると,
をとると,
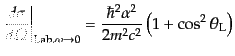 |
(H.7.486) |
となり,偏極のない場合のトムソン散乱断面積に帰着する.この式を全立体角
で積分した全断面積
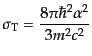 |
(H.7.487) |
は全トムソン断面積である.
Footnotes
- ...は微細構造定数とよばれる無次元量であるH12
- ここでは
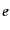 はローレンツ・ヘビサイド単位系での単位電荷であり、SI単位系では
はローレンツ・ヘビサイド単位系での単位電荷であり、SI単位系では
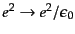 と読みかえる.
と読みかえる.
- ... formula)H13
- O. Klein and Y. Nishina, Z. Phys. 52, 853
(1929)





次へ: 相対論的運動学
上へ: 場の量子化と粒子の相互作用
前へ: 量子場の相互作用
目次
索引
All rights reserved © T.Matsubara 2004-2010
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11
![]() とするとき,式(8.4.189)で
とするとき,式(8.4.189)で![]() とおい
たもので与えられ,電子と光子の相互作用部分は正規積の規約を考慮に入れて,
とおい
たもので与えられ,電子と光子の相互作用部分は正規積の規約を考慮に入れて,
![]() において,数密度
において,数密度![]() , 速度
, 速度![]() をもつ電子のビームがある
運動量体積素片
をもつ電子のビームがある
運動量体積素片![]() の終状態へ散乱される回数を
の終状態へ散乱される回数を![]() とするとき,この
終状態への微分散乱断面積
とするとき,この
終状態への微分散乱断面積![]() は
は
![]() はダイソンの公式
(8.6.317)を展開して計算する.
はダイソンの公式
(8.6.317)を展開して計算する.
![]() に関して展開
した摂動の
に関して展開
した摂動の![]() 次の項を
次の項を![]() と表記すると,
と表記すると,
![]() とかく.いま摂動の0次の項は相互作用がない場合と同じで全く散乱
されない状況を表すので,
とかく.いま摂動の0次の項は相互作用がない場合と同じで全く散乱
されない状況を表すので,
![]() につい
ては平均をとる.また,散乱電子の偏極は測られないので,終状態のスピン
につい
ては平均をとる.また,散乱電子の偏極は測られないので,終状態のスピン
![]() については和をとることになる.したがって偏極なしの微分散乱断面積
は
については和をとることになる.したがって偏極なしの微分散乱断面積
は
![]() とし
たもの,また重心系では式(8.6.358)で与えられる.始状態
とし
たもの,また重心系では式(8.6.358)で与えられる.始状態
![]() と終状態
と終状態
![]() は
は
![]() に含ま
れている生成演算子と交換し,どんどん右側へと移動させる.そして一番右に
その消滅演算子が来て
に含ま
れている生成演算子と交換し,どんどん右側へと移動させる.そして一番右に
その消滅演算子が来て
![]() にかかって消えるまで続ける.このプロセス
において移動される消滅演算子は始状態の生成演算子のどれかひとつとペアを
つくって定数項を出し,それらがおつりの項として消えずに残ることになる.
ここでもし,始状態の生成演算子とペアをつくるのに十分な数の消滅演算子が
なければ,始状態の生成演算子のどれかはそのまま残されるが,それはS行列
演算子の中の生成演算子と反交換して終状態の消滅演算子のすぐ右側に到達す
る.ここで始状態にある粒子と同じ状態の粒子が終状態にあるとすると,それ
は散乱されなかったことを意味するから,散乱が起こったときの断面積を考え
る限り始状態の生成演算子は終状態の消滅演算子と反交換する.したがってS
行列を通り越してしまった始状態の生成演算子は
にかかって消えるまで続ける.このプロセス
において移動される消滅演算子は始状態の生成演算子のどれかひとつとペアを
つくって定数項を出し,それらがおつりの項として消えずに残ることになる.
ここでもし,始状態の生成演算子とペアをつくるのに十分な数の消滅演算子が
なければ,始状態の生成演算子のどれかはそのまま残されるが,それはS行列
演算子の中の生成演算子と反交換して終状態の消滅演算子のすぐ右側に到達す
る.ここで始状態にある粒子と同じ状態の粒子が終状態にあるとすると,それ
は散乱されなかったことを意味するから,散乱が起こったときの断面積を考え
る限り始状態の生成演算子は終状態の消滅演算子と反交換する.したがってS
行列を通り越してしまった始状態の生成演算子は
![]() にかかって消えて
しまう.したがって,S行列演算子の右側に出てくる消滅演算子は必ず始状態
の粒子と同じ数だけなければならない(そうでなければ少なくともひとつの粒
子は散乱されない)ということになる.以上と同じことがS行列演算子の左側に
ある生成演算子についてもいえる.したがって,S行列演算子のウィックの定
理による展開においては,そこから出る生成消滅演算子がかならず始状態およ
び終状態の粒子とペアを作らなければならないことがわかる.
にかかって消えて
しまう.したがって,S行列演算子の右側に出てくる消滅演算子は必ず始状態
の粒子と同じ数だけなければならない(そうでなければ少なくともひとつの粒
子は散乱されない)ということになる.以上と同じことがS行列演算子の左側に
ある生成演算子についてもいえる.したがって,S行列演算子のウィックの定
理による展開においては,そこから出る生成消滅演算子がかならず始状態およ
び終状態の粒子とペアを作らなければならないことがわかる.
![]() ,
,
![]() に関する縮約を全く含まない項と,
に関する縮約を全く含まない項と,
![]() の縮約された項のみである.しかも,陽電子に関する項はすべて落ち
るから,
の縮約された項のみである.しかも,陽電子に関する項はすべて落ち
るから,![]() の正振動部分,
の正振動部分,
![]() の負振動部分のみが生き残
る.したがって,
の負振動部分のみが生き残
る.したがって,
![]() 行列
行列
![]() があるとき,
があるとき,
![]() ,
,
![]() ,
,
![]() を用いると
を用いると
![]() 行列のトレースの計算ができれば散乱断面積が求められる
ことになる.この目的のため,ここで有用なトレース計算の技術をまとめてお
く.まず,式(8.4.132)-(8.4.134)と
行列のトレースの計算ができれば散乱断面積が求められる
ことになる.この目的のため,ここで有用なトレース計算の技術をまとめてお
く.まず,式(8.4.132)-(8.4.134)と
![]() を
くり返し使って証明できる公式
を
くり返し使って証明できる公式
![]() 行列の反交換
関係(8.4.132)をくり返し使って得られる次の公式である:
行列の反交換
関係(8.4.132)をくり返し使って得られる次の公式である:
![]() 行列は縮約公式(8.7.425)-(8.7.429)を用いて行列
の数を減らし,あとはトレース公式(8.7.413)-(8.7.418)を
使ってトレースを計算していけばよい.例えば,行列のもっとも多い項として
式(8.7.412)のうち,8個の行列の積の計算は次のようになる:
行列は縮約公式(8.7.425)-(8.7.429)を用いて行列
の数を減らし,あとはトレース公式(8.7.413)-(8.7.418)を
使ってトレースを計算していけばよい.例えば,行列のもっとも多い項として
式(8.7.412)のうち,8個の行列の積の計算は次のようになる:
![]() に置き換えれば
散乱断面積を一般的に得るが,いま2体反応なので重心系で記述することによ
り,より便利な式を得ることができる.重心系では
に置き換えれば
散乱断面積を一般的に得るが,いま2体反応なので重心系で記述することによ
り,より便利な式を得ることができる.重心系では
![]() ,
,
![]() , また,
, また,
![]() となる.したがって,重心系での2体反応の散
乱断面積の式(8.6.357)は
となる.したがって,重心系での2体反応の散
乱断面積の式(8.6.357)は
![]() に含まれる演算子,あるいは始状態と終状態の生成消滅演
算子をペアにしていく作業であることがわかる.ここで,
に含まれる演算子,あるいは始状態と終状態の生成消滅演
算子をペアにしていく作業であることがわかる.ここで,
![]() 同士のペアからは伝播関数が発生し,
同士のペアからは伝播関数が発生し,
![]() と始状態,終状態の
間のペアからは演算子の平面波展開の係数(上の場合
と始状態,終状態の
間のペアからは演算子の平面波展開の係数(上の場合
![]() や
や
![]() )が発生する.このことからまず,始状態や生成演算子が相互作用から出
る消滅演算子とペアをつくることに対して,始状態の粒子を図8.3で
表されるような外線に対応させる.
)が発生する.このことからまず,始状態や生成演算子が相互作用から出
る消滅演算子とペアをつくることに対して,始状態の粒子を図8.3で
表されるような外線に対応させる.
![]() が
つながっている頂点ではそのフーリエ変換
が
つながっている頂点ではそのフーリエ変換
![]() を使い,
を使い,
![]() 軸をとると
軸をとると
![]() ,
,
![]() となる.この座標で偏極ベクトルとして式
(8.4.195)-(8.4.199)のようにとる.すると,偏極ベクトル
は実の量であり,また横偏極ベクトルは
となる.この座標で偏極ベクトルとして式
(8.4.195)-(8.4.199)のようにとる.すると,偏極ベクトル
は実の量であり,また横偏極ベクトルは![]() ,
, ![]() 成分しか持たないから,入射
光子の横偏極ベクトルは入射粒子のどちらとも垂直になる:
成分しか持たないから,入射
光子の横偏極ベクトルは入射粒子のどちらとも垂直になる:
![]() 行
列の順序を反交換関係により交換して計算すると,
行
列の順序を反交換関係により交換して計算すると,
![]() ,
,
![]() などのように略記する.計算の方針は
などのように略記する.計算の方針は![]() 行
列の反交換関係(8.4.132)を用いて変形して
行
列の反交換関係(8.4.132)を用いて変形して![]() 行列の数をなる
べく減らしていくことである.つまり,式(8.7.430),
(8.7.431)
行列の数をなる
べく減らしていくことである.つまり,式(8.7.430),
(8.7.431)
![]() と置き換えたものなので,式
(8.7.454)まではこの置き換えによる式がそのまま成り立つ.
と置き換えたものなので,式
(8.7.454)まではこの置き換えによる式がそのまま成り立つ.
![]() 方向へはローレンツ変換を受けないので,
重心系と実験室系の散乱立体角をそれぞれ
方向へはローレンツ変換を受けないので,
重心系と実験室系の散乱立体角をそれぞれ
![]() ,
,
![]() とすると,その変換のヤコビアンは
とすると,その変換のヤコビアンは
![]() であることが従い,これと式(8.7.469)から,
であることが従い,これと式(8.7.469)から,
![]() ,
,
![]() はそれぞれ
はそれぞれ
![]() ,
,
![]() に垂直な単位ベクトルである.そこで入射光子の波数ベクトルに
より,式(8.4.197)-(8.4.199)のように作った完全系,
に垂直な単位ベクトルである.そこで入射光子の波数ベクトルに
より,式(8.4.197)-(8.4.199)のように作った完全系,
![]() (
(![]() )および,散乱光子の波数ベクトルにより
作った
)および,散乱光子の波数ベクトルにより
作った
![]() (
(![]() )を導入する.どちらも完全系をな
すので,
)を導入する.どちらも完全系をな
すので,
![]() ,
,
![]() および,プライムのついた同様の式が成り立つ.このことを用い
ると,偏極ベクトルの部分は次のように計算できる:
および,プライムのついた同様の式が成り立つ.このことを用い
ると,偏極ベクトルの部分は次のように計算できる:
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11