




次へ: ボルツマン方程式
上へ: 相対論的運動学
前へ: 相対論的運動学
目次
索引
粒子の運動を統計的に扱うため,ある粒子種について位相空間中の分布関数
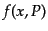 を考える.ここで,
を考える.ここで,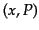 は時空座標
は時空座標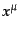 および4元運動量
および4元運動量
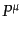 からなる8次元空間を表している.時空の不変体積素片は
からなる8次元空間を表している.時空の不変体積素片は
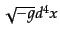 である.4元運動量もベクトルとして変換するので,その不
変体積素片も同様に
である.4元運動量もベクトルとして変換するので,その不
変体積素片も同様に
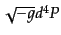 である.したがって,位相空間の不変体
積素片は
である.したがって,位相空間の不変体
積素片は
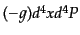 となる.このとき,粒子の質量を
となる.このとき,粒子の質量を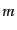 とすると,4元運
動量は
とすると,4元運
動量は
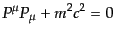 |
(I.1.1) |
を満たす.この関係のことを指して,4元運動量は質量殻上にある,という.
したがって,位相空間の実際の物理的な自由度は7である.また,粒子のエネ
ルギー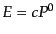 は正でなければならない.そこで,運動量空間の物理的な3
次元の不変運動量素片として,次の量を定義する:
は正でなければならない.そこで,運動量空間の物理的な3
次元の不変運動量素片として,次の量を定義する:
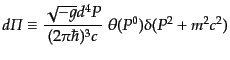 |
(I.1.2) |
座標変換によってエネルギーの符合が変わることはないので,左辺は一般座標
変換に対してスカラーである.これは,局所ミンコフスキー空間においては,
という具体的な形となる.ただし,最後の式ではエネルギー
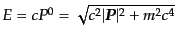 を従属変数と考えている.左辺はスカラー
なので,最後の式も(この局所ミンコフスキー空間で)スカラーである.
を従属変数と考えている.左辺はスカラー
なので,最後の式も(この局所ミンコフスキー空間で)スカラーである.
さまざまな巨視的変数は分布関数の平均量として表すことができる.まず,粒
子の数密度がどう表されるか考えてみよう.局所ミンコフスキー空間では,分
布関数を単に運動量で積分すれば数密度になることが明らかである:
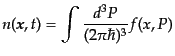 |
(I.1.4) |
したがって,一般座標では次のようになる:
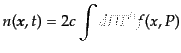 |
(I.1.5) |
この量は,ベクトル量の時間成分となっていることがわかる.そこで,次のベ
クトルを定義する:
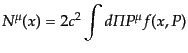 |
(I.1.6) |
この4元ベクトルを,粒子4元流束(particle 4-flow)と呼ぶ.このベク
トルの時間成分と空間成分を
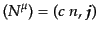 |
(I.1.7) |
と書いてみる.時間成分は上で見たように粒子数密度である.空間成分を局所
ミンコフスキー空間で表してみると,
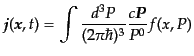 |
(I.1.8) |
となる.ここで,
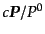 は粒子の3次元速度であるから,上式は粒子
の平均的な空間方向の流れを表す量となっている.すなわち,粒子4元流束
は粒子の3次元速度であるから,上式は粒子
の平均的な空間方向の流れを表す量となっている.すなわち,粒子4元流束
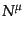 は粒子の数密度と空間方向の平均速度から作られるベクトル量である
ことがわかる.
は粒子の数密度と空間方向の平均速度から作られるベクトル量である
ことがわかる.
エネルギー運動量テンソルも同様に分布関数の積分で表すことができる.その
ため,まずは局所ミンコフスキー空間において考えてみる.はじめに,
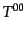 はエネルギー密度である.これは,1粒子あたりのエネルギー
はエネルギー密度である.これは,1粒子あたりのエネルギー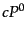 を運動量平均することにより,
を運動量平均することにより,
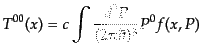 |
(I.1.9) |
と表されることがわかる.次に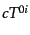 は
は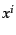 一定の面を横切るエネルギー
の流れであるから,
一定の面を横切るエネルギー
の流れであるから,
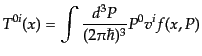 |
(I.1.10) |
となる.ここで,
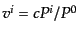 は粒子の3次元速度である.また,
は粒子の3次元速度である.また,
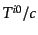 は運動量
は運動量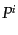 の平均値であるから,
の平均値であるから,
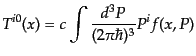 |
(I.1.11) |
である.最後に,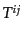 は
は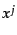 方向への運動量
方向への運動量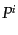 の流れであるから,
の流れであるから,
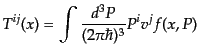 |
(I.1.12) |
エネルギー運動量テンソルはテンソルなので,上に求めた各成分はまとめて簡
単な形になるだろうことは容易に想像できるだろう。実際,次のように共変な
形で表すことができる:
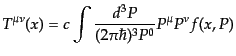 |
(I.1.13) |
つまり,エネルギー運動量テンソルは分布関数の2次のモーメントである.こ
れを一般座標で表せば,
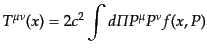 |
(I.1.14) |
となる.
非平衡系におけるエントロピー密度は局所ミンコフスキー空間の分布関数によ
り次の積分で定義される.
![$\displaystyle S^0(x) = - k_{\rm B}c \int \frac{d^3P}{(2\pi\hbar)^3} f(x,P) \left[\ln f(x,P) - 1\right]$](img2511.png) |
(I.1.15) |
また,エントロピーの流れは
![$\displaystyle {\mbox{\boldmath$S$}}(x) = - k_{\rm B} \int \frac{d^3P}{(2\pi\hbar)^3} {\mbox{\boldmath$u$}} f(x,P) \left[\ln f(x,P) - 1\right]$](img2512.png) |
(I.1.16) |
である.これらをまとめて、4元ベクトルの形にし,さらに一般座標で表せば,
![$\displaystyle S^\mu(x) = - 2 k_{\rm B} c^2 \int d{\mit\Pi}P^\mu f(x,P) \left[\ln f(x,P) - 1\right]$](img2513.png) |
(I.1.17) |
これをエントロピーの4元流束という.





次へ: ボルツマン方程式
上へ: 相対論的運動学
前へ: 相対論的運動学
目次
索引
All rights reserved © T.Matsubara 2004-2010
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11
![]() を考える.ここで,
を考える.ここで,![]() は時空座標
は時空座標![]() および4元運動量
および4元運動量
![]() からなる8次元空間を表している.時空の不変体積素片は
からなる8次元空間を表している.時空の不変体積素片は
![]() である.4元運動量もベクトルとして変換するので,その不
変体積素片も同様に
である.4元運動量もベクトルとして変換するので,その不
変体積素片も同様に
![]() である.したがって,位相空間の不変体
積素片は
である.したがって,位相空間の不変体
積素片は
![]() となる.このとき,粒子の質量を
となる.このとき,粒子の質量を![]() とすると,4元運
動量は
とすると,4元運
動量は
![]() はエネルギー密度である.これは,1粒子あたりのエネルギー
はエネルギー密度である.これは,1粒子あたりのエネルギー![]() を運動量平均することにより,
を運動量平均することにより,
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11