




次へ: 宇宙パラメータ
上へ: フリードマン・ルメートルモデル
前へ: フリードマン・ルメートルモデル
目次
索引
スケール因子を除いたRW計量の空間部の3次元計量を
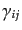 とすると,
RW計量は
とすると,
RW計量は
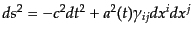 |
(C.1.1) |
とかける.ここで,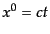 ,
, 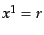 ,
,
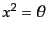 ,
,
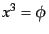 という座標をとってあるとすると,
という座標をとってあるとすると,
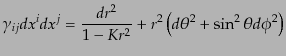 |
(C.1.2) |
であるが,この3次元計量は行列表示で
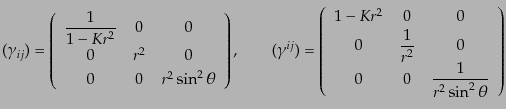 |
(C.1.3) |
であり,この記法で4次元計量は
![$\displaystyle (g_{\mu\nu}) = \left[ \begin{array}{cc} - 1 & 0 0 & a^2 (\gamm...
...cc} - 1 & 0 0 & \displaystyle \frac{1}{a^2}(\gamma^{ij}) \end{array} \right]$](img230.png) |
(C.1.4) |
である.
このように計量を時間部分と空間部分に分けることにより,クリストッフェル
記号は比較的容易に計算できて,
となる.同様に曲率テンソルを求めることができるが,対称性からは明らかで
ない成分のみに限って結果を書き下せば,
さらにリッチテンソルは
また,スカラー曲率は
![$\displaystyle R = \frac{6}{c^2} \left[\frac{\ddot{a}}{a} + \left(\frac{\dot{a}}{a}\right)^2 + \frac{c^2}{a^2} K \right]$](img240.png) |
(C.1.8) |
となる.これらによりアインシュタインテンソルを求めれば,
となる.アインシュタイン方程式
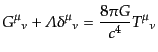 |
(C.1.10) |
からただちにエネルギー運動量テンソルが
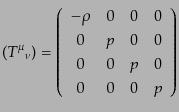 |
(C.1.11) |
という形しかとり得ないことがわかる.これは理想流体のエネルギー運動量テ
ンソルの形であり,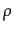 はエネルギー密度に,
はエネルギー密度に,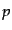 は圧力に相当する.非等
方ストレスに寄与する粘性や熱伝導はいまの場合存在し得ない.これはわれわ
れが宇宙に一様等方性を課した結果,エネルギーや運動量の空間方向への流れ
が禁止されていることに対応している.すると,アインシュタイン方程式の時
間成分と空間成分は,次の2つの方程式となる:
は圧力に相当する.非等
方ストレスに寄与する粘性や熱伝導はいまの場合存在し得ない.これはわれわ
れが宇宙に一様等方性を課した結果,エネルギーや運動量の空間方向への流れ
が禁止されていることに対応している.すると,アインシュタイン方程式の時
間成分と空間成分は,次の2つの方程式となる:
これがRW計量を変数を力学的に規定するのアインシュタイン方程式であり,式
(3.1.12)を特にフリードマン方程式 (Friedmann
equation) という.これらと独立ではないが,保存則
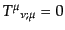 の時間成分から,次の式が導かれる:
の時間成分から,次の式が導かれる:
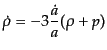 |
(C.1.14) |
式(3.1.12)を微分して式(3.1.13)から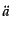 を消去するこ
とによってもこの式は導かれる.この式は,物理的に物質のエントロピーが保
存することを表している.これを見るため,宇宙の膨張とともに膨らんでいく
共動体積
を消去するこ
とによってもこの式は導かれる.この式は,物理的に物質のエントロピーが保
存することを表している.これを見るため,宇宙の膨張とともに膨らんでいく
共動体積
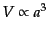 を考え,その体積中のエントロピーを
を考え,その体積中のエントロピーを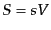 とする.
ここで
とする.
ここで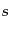 は単位体積あたりのエントロピーである.
この体積中のエネルギーは
は単位体積あたりのエントロピーである.
この体積中のエネルギーは
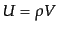 で表される.さらにこの体積中に存在
する粒子種
で表される.さらにこの体積中に存在
する粒子種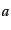 の粒子数を
の粒子数を
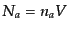 とする.ここで
とする.ここで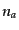 は対応する粒子
の数密度である.この粒子の化学ポテンシャルを
は対応する粒子
の数密度である.この粒子の化学ポテンシャルを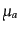 とする.すると,温
度を
とする.すると,温
度を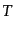 として,熱力学第一法則により
として,熱力学第一法則により
![$\displaystyle \frac{dS}{dt} = \frac{1}{T} \left( \frac{dU}{dt} + p\frac{dV}{dt}...
... 3\frac{\dot{a}}{a} (\rho + p) \right] - \sum_a \frac{\mu_a}{T} \frac{dN_a}{dt}$](img264.png) |
(C.1.15) |
となるが,この式の左辺第一項は式(3.1.14)からゼロである.したがっ
て,粒子数が保存して
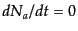 が成り立っているときには共動体積中
のエントロピーが保存する.これは一様等方宇宙においては空間的に熱が流れ
ることがありえないため,断熱的にふるまうからである.
また,粒子数の保存しない反応が起きているとき
でも,化学ポテンシャルが小さく
が成り立っているときには共動体積中
のエントロピーが保存する.これは一様等方宇宙においては空間的に熱が流れ
ることがありえないため,断熱的にふるまうからである.
また,粒子数の保存しない反応が起きているとき
でも,化学ポテンシャルが小さく
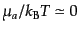 が成り立っ
ていればやはりエントロピーは近似的に保存することになる.実際の宇宙の進
化に表れてくる様々な粒子については
が成り立っ
ていればやはりエントロピーは近似的に保存することになる.実際の宇宙の進
化に表れてくる様々な粒子については
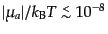 程度になっていて,化学ポテンシャルは無視することが可能である.したがっ
て宇宙のエントロピーは保存すると考えてよい.
程度になっていて,化学ポテンシャルは無視することが可能である.したがっ
て宇宙のエントロピーは保存すると考えてよい.
膨張宇宙では,ある共動体積に注目すると断熱膨張をしているため,必ずしも
その中で粒子のエネルギーは保存しない.ネーターの定理によれば,物質のエ
ネルギー保存則は時間についての系の並進対称性の現れである.いま,膨張宇
宙では物質にとってこの対称性がない.膨張宇宙ではエネルギーの代わりに,
物質のエントロピーが保存するのである.ただし,開いた系では一般に式
(3.1.15)左辺はエントロピーの微分ではない.この場合には後にみるよ
うに,化学ポテンシャルが粒子のエネルギーに比べて無視できないような異常
に強い相互作用をする粒子が生成消滅するような宇宙では,一般にはエントロ
ピーも保存しない.
さて,独立な方程式として,フリードマン方程式(3.1.12)と保存則
(3.1.14)の2つがある.曲率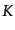 と宇宙定数
と宇宙定数
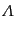 が与えられれば,
未知変数は
が与えられれば,
未知変数は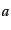 ,
, 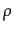 ,
, 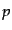 の3つであり,このままでは解けない.これは宇
宙の中の物質を指定していないからである.この他に物質の状態方程式
の3つであり,このままでは解けない.これは宇
宙の中の物質を指定していないからである.この他に物質の状態方程式
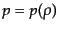 があれば,それと保存則(3.1.15)からエネルギー密度とスケー
ル因子の関係
があれば,それと保存則(3.1.15)からエネルギー密度とスケー
ル因子の関係
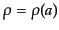 が求まり,さらにこれをフリードマン方程式
(3.1.12)へ入れれば,スケール因子の時間変化
が求まり,さらにこれをフリードマン方程式
(3.1.12)へ入れれば,スケール因子の時間変化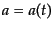 が求められ
ることになる.ここで1階微分方程式を2度解くことになるので,境界条件が
2つ必要である.これは現在の変数の値
が求められ
ることになる.ここで1階微分方程式を2度解くことになるので,境界条件が
2つ必要である.これは現在の変数の値
 ,
,
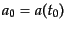 とすればよいが,スケール因子には規格化
とすればよいが,スケール因子には規格化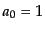 を採用してあるの
で,
を採用してあるの
で,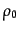 のみ指定すればよいことになる.これと曲率
のみ指定すればよいことになる.これと曲率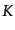 と宇宙定数
と宇宙定数
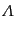 の3つを与えれば一様等方時空の進化が一意的に定まることになる.
の3つを与えれば一様等方時空の進化が一意的に定まることになる.





次へ: 宇宙パラメータ
上へ: フリードマン・ルメートルモデル
前へ: フリードマン・ルメートルモデル
目次
索引
All rights reserved © T.Matsubara 2004-2010
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11
![]() とすると,
RW計量は
とすると,
RW計量は
![]() と宇宙定数
と宇宙定数
![]() が与えられれば,
未知変数は
が与えられれば,
未知変数は![]() ,
, ![]() ,
, ![]() の3つであり,このままでは解けない.これは宇
宙の中の物質を指定していないからである.この他に物質の状態方程式
の3つであり,このままでは解けない.これは宇
宙の中の物質を指定していないからである.この他に物質の状態方程式
![]() があれば,それと保存則(3.1.15)からエネルギー密度とスケー
ル因子の関係
があれば,それと保存則(3.1.15)からエネルギー密度とスケー
ル因子の関係
![]() が求まり,さらにこれをフリードマン方程式
(3.1.12)へ入れれば,スケール因子の時間変化
が求まり,さらにこれをフリードマン方程式
(3.1.12)へ入れれば,スケール因子の時間変化![]() が求められ
ることになる.ここで1階微分方程式を2度解くことになるので,境界条件が
2つ必要である.これは現在の変数の値
が求められ
ることになる.ここで1階微分方程式を2度解くことになるので,境界条件が
2つ必要である.これは現在の変数の値
![]() ,
,
![]() とすればよいが,スケール因子には規格化
とすればよいが,スケール因子には規格化![]() を採用してあるの
で,
を採用してあるの
で,![]() のみ指定すればよいことになる.これと曲率
のみ指定すればよいことになる.これと曲率![]() と宇宙定数
と宇宙定数
![]() の3つを与えれば一様等方時空の進化が一意的に定まることになる.
の3つを与えれば一様等方時空の進化が一意的に定まることになる.
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11