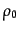 ,
, 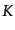 ,
,
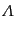 の関数のことを宇宙パラメータという.もちろん無限に関数を作
ることができるので,宇宙パラメータはいくらでもあるが,以下に代表的なも
のを示す.
の関数のことを宇宙パラメータという.もちろん無限に関数を作
ることができるので,宇宙パラメータはいくらでもあるが,以下に代表的なも
のを示す.
RW計量のアインシュタイン方程式における3つの未定の定数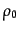 ,
, 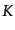 ,
,
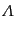 の関数のことを宇宙パラメータという.もちろん無限に関数を作
ることができるので,宇宙パラメータはいくらでもあるが,以下に代表的なも
のを示す.
の関数のことを宇宙パラメータという.もちろん無限に関数を作
ることができるので,宇宙パラメータはいくらでもあるが,以下に代表的なも
のを示す.
ハッブル定数は
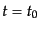 とおけば,
とおけば,
規格化された量として
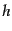 が使われることが多い.ハッブル定数の観測的な見積もり
としては現在のところ,
が使われることが多い.ハッブル定数の観測的な見積もり
としては現在のところ,
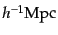 のような組み合わ
せを距離の単位として用いることにより,ハッブル定数の不定性を表面に現れ
ないようにして取り扱うことが多い.式(3.2.18)のように
のような組み合わ
せを距離の単位として用いることにより,ハッブル定数の不定性を表面に現れ
ないようにして取り扱うことが多い.式(3.2.18)のように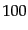 で規格
化しない場合もあり,例えば
で規格
化しない場合もあり,例えば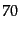 で規格化した場合
で規格化した場合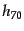 などの記号を用い
ることもある.
などの記号を用い
ることもある.
曲率も宇宙定数もないような宇宙における現在の密度のことを臨界密度
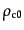 という.式(3.2.17)からそれは
という.式(3.2.17)からそれは
臨界密度に対する現実の宇宙の質量密度の割合を密度パラメータ
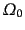 と呼ぶ.すなわち,
と呼ぶ.すなわち,
宇宙定数をハッブル定数などにより,次のようにスケールしたものをスケール
された宇宙定数
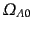 と呼ぶ:
と呼ぶ:
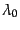 という記
号で表されることもある.
という記
号で表されることもある.
同様に,曲率をスケールしたものを曲率パラメータ
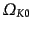 と呼ぶ:
と呼ぶ:
宇宙膨張の減速を表す無次元化した量として,
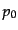 は状態方程式により
は状態方程式により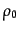 で表される.
で表される.
宇宙パラメータの独立量は3つであるから,これらいくつものパラメータの間
には関係がある.特に有用な関係式として,
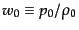 は状態方程式から出るパラメータ
である.
は状態方程式から出るパラメータ
である.
上のように現在値でフリードマン方程式の境界条件を指定することが一般的で
あるが,特に現在値である必要はない.現在に近い宇宙を観測する場合には現
在値をとることが自然であるが,深宇宙の観測をする場合は現在値を特別視す
る必然性もなく,観測している天体などに対応する過去の時刻を使うほうが自
然な場合もある.任意の時刻においても宇宙パラメータを定義することができ,
これを時間に依存する宇宙パラメータと呼ぶ.それらは,以下のように定義さ
れる:
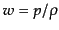 である.
である.
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11