




次へ: 諸成分ゆらぎの進化 II: 強結合近似とゆらぎの成長
上へ: 摂動の線形成長
前へ: 宇宙の諸成分ゆらぎの発展方程式
目次
索引
諸成分ゆらぎの進化 I: 超ホライズンスケール
ここまでで,ダークマター,ニュートリノ,光子,バリオンからなる宇宙のゆ
らぎの線形成長をつかさどる閉じた発展方程式が得られたが,巨大な連立微分
方程式となっているためその正確な解を得るには数値的に解く必要がある.だ
が,そうして得られた解を見ても,摂動の成長の物理過程がすぐにはよくわか
らない.そこで以下ではゆらぎの成長の発展方程式を近似を用いて解析的に解
き,その物理的振舞いを理解する.ここではコールドダークマターモデルを考
え,ニュートリノの質量はゆらぎの成長には無視できるほど小さいものとする.
ホライズン内のゆらぎの成長は粒子間相互作用により比較的複雑な振る舞いを
する.一方,超ホライズンスケールには粒子間相互作用がないので,ゆらぎの
振舞いは比較的簡単である.この場合,粒子種の違いはそれが相対論的か非相
対論的かということがもっとも重要であり、おおまかには節12.3の
議論でほぼゆらぎの成長が表される.ホライズン内のゆらぎも,時間を初期に遡
ればはじめは超ホライズンスケールにあったので,超ホライズンスケールのゆ
らぎはホライズン内のゆらぎに対しては初期条件と考えることができる.そこ
で,いま考えている多成分系において,超ホライズンスケールのゆらぎの成長
をもうすこし詳しく調べてみる.特に節12.3で無視されていた非等
方ストレスの補正をここで考えておく.非相対論的成分であるコールドダーク
マターとバリオンには非等方ストレスはない.また,光子の非等方ストレスは
このあとで示すように,トムソン散乱によって小さくなっていて,無視し得る.
そこで,非等方ストレスには主にニュートリノが寄与することになる.この場
合,式(10.7.239)により,
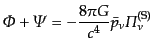 |
(L.5.243) |
となる.節12.3と同様に,等密度時を基準にしたスケール因子を
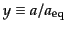 とすると,全密度は
とすると,全密度は
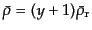 となる.ここで,放射成分はいま光子とニュートリノ
で成り立ち,
となる.ここで,放射成分はいま光子とニュートリノ
で成り立ち,
 である.ここで,初期宇宙を考えているので
である.ここで,初期宇宙を考えているので
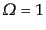 であることと,式
(10.4.75), (12.3.75)および
であることと,式
(10.4.75), (12.3.75)および
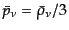 を用いると,
を用いると,
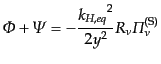 |
(L.5.244) |
となる.ただし,
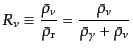 |
(L.5.245) |
は全放射エネルギー成分に対するニュートリノのエネルギー成分の比である.
この比は時間的に一定で,現在のニュートリノの光子に対するエネルギー比に
より,
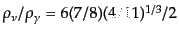 となるから,
となるから,
![$\displaystyle R_\nu = \left[1 + \frac{8}{21}\left(\frac{11}{4}\right)^{4/3}\right]^{-1} \simeq 0.405$](img4148.png) |
(L.5.246) |
と求められる.
このようにニュートリノの非等方ストレスが2つのポテンシャルに差を生じさ
せることになる.この非等方ストレスの進化はポテンシャルの進化と独立では
ないため,一般解を求めるのは難しい.だが,非等方ストレス自体は小さい量
であるから,これを無視した節12.3の結果を0次解として,その効
果を摂動として取り入れることを考える.つまり,0次解のポテンシャルのも
とで非等方ストレスを求め,それを式(12.5.249)に用いてポテンシャ
ルの補正を求める.
ニュートリノの非等方ストレスを決める方程式は式(12.4.130)で与え
られている.ここで,初期には超ホライズンスケールで高次の多重極成分は励
起していないものとすると,
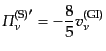 |
(L.5.247) |
となる.ここで,超ホライズンスケールでは因果律により,成分間で速度差が
生じることはない.そこで,上式の右辺は物質全体の速度
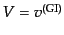 と同一視することができる.すると式(10.5.197)により,
と同一視することができる.すると式(10.5.197)により,
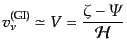 |
(L.5.248) |
で与えられる.このことと,
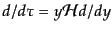 であること,および式
(12.3.75)により,式(12.5.252)は
であること,および式
(12.3.75)により,式(12.5.252)は
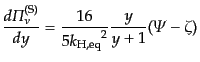 |
(L.5.249) |
とかける.この方程式の右辺に非等方ストレスを無視した0次解を代入して積
分すれば非等方ストレスの1次解が求まることになる.
はじめに断熱ゆらぎを考える。放射優勢期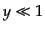 の場合に0次解,
の場合に0次解,
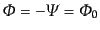 ,
,
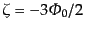 を用いて積分すれば,
を用いて積分すれば,
 |
(L.5.250) |
となるので,式(12.5.249)から,
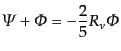 |
(L.5.251) |
となる.ただし,右辺
のポテンシャルの表式に0次解を入れ直したが,これは右辺全体が非等方スト
レスの摂動の1次であることから正当化される.また,物質優勢期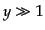 の0次解
の0次解
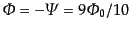 ,
,
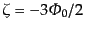 を用いて積分すれば,
を用いて積分すれば,
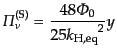 |
(L.5.252) |
となるので,
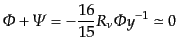 |
(L.5.253) |
である.以上をまとめると,超ホライズンスケールのポテンシャルについて、
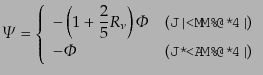 |
(L.5.254) |
の関係にある.非等方ストレスを無視した場合に比べて,放射優勢期のポテン
シャルに10%程度の差が生じることがわかる.
上で述べたように,どのようなスケールのゆらぎも初めは超ホライズンスケー
ルを経ているので,
超ホライズンスケールのポテンシャルの振る舞いはホライズン内のゆらぎの振
る舞いに対する初期条件を与えることになる.物質優勢期にホライズン内に入
るゆらぎの成長は比較的単調であるが,放射優勢期にホライズン内に入る小ス
ケールのゆらぎの振る舞いはより複雑である.そこで,後者の場合のポテンシャ
ルの初期条件を考えれば,
| |
|
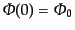 |
(L.5.255) |
| |
|
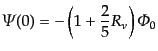 |
(L.5.256) |
で与えられることになる.
等曲率ゆらぎの場合にも対応する初期条件を求めるため,放射優勢期の0次解
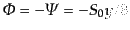 ,
,
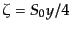 を用いる.すると,
を用いる.すると,
 |
(L.5.257) |
となるので,
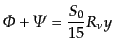 |
(L.5.258) |
である.これだけではポテンシャルがエントロピーゆらぎの初期値だけからは
定まらないので,曲率ゆらぎの発展方程式(10.6.200)を考えてみる.
ここで非等方ストレスの有無にかかわらず成り立つ式
(12.3.73)-(12.3.75), (12.3.79), (10.4.168)を
使い,さらに式(12.5.262)も用いてから放射優勢期の極限をとれば,
密度ゆらぎと非等方ストレスの項はこの極限で消え,
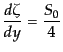 |
(L.5.259) |
が導かれる.すなわち,
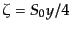 は非等方ストレスがあっても成立
している.そこで,曲率ゆらぎをポテンシャルで表した式
(10.6.198)から,
は非等方ストレスがあっても成立
している.そこで,曲率ゆらぎをポテンシャルで表した式
(10.6.198)から,
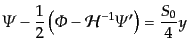 |
(L.5.260) |
が成立する.式(12.5.263)と式(12.5.265)を連立させてポ
テンシャルについて解くことにより,
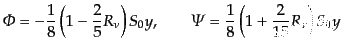 |
(L.5.261) |
と求まる.当然ながら
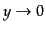 でポテンシャルの初期値はゼロであ
り,初期条件としては微分形で与えられる:
でポテンシャルの初期値はゼロであ
り,初期条件としては微分形で与えられる:
| |
|
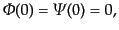 |
(L.5.262) |
| |
|
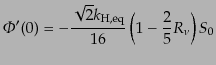 |
(L.5.263) |
| |
|
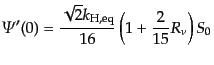 |
(L.5.264) |
さらに諸成分のゆらぎの初期条件を考える.まず,式(10.4.151)から,
超ホライズンの極限
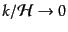 で全密度ゆらぎに対して
で全密度ゆらぎに対して
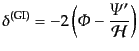 |
(L.5.265) |
が得られる.この左辺の全密度ゆらぎはいま
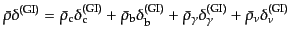 |
(L.5.266) |
で与えられる.
ニュートリノの脱結合よりも以前にゆらぎが生成されていれば光子と
ニュートリノの密度ゆらぎは等しくなり,
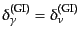 である.また,式(12.4.247)において係数
である.また,式(12.4.247)において係数
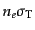 は光子の平均自由行程の逆数である.一方,左辺は,超
ホライズンスケールの逆数の変化であるから,右辺の括弧内は非常に小さくな
くてはならず,
は光子の平均自由行程の逆数である.一方,左辺は,超
ホライズンスケールの逆数の変化であるから,右辺の括弧内は非常に小さくな
くてはならず,
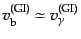 となる.
このとき,(12.4.217), (12.4.246)から,
となる.
このとき,(12.4.217), (12.4.246)から,
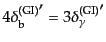 となるが,
これはバリオン-エントロピー比
となるが,
これはバリオン-エントロピー比
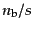 のゆらぎが時間変化しないことを意味する.なぜなら式
(12.3.80)と同様にして
のゆらぎが時間変化しないことを意味する.なぜなら式
(12.3.80)と同様にして
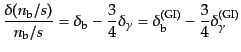 |
(L.5.267) |
となるからである.すなわち,ゆらぎの成長は断熱的となる.バリオン-エン
トロピー比は温度に依らないのでゆらぎの生成時には空間的に一定値をとると
考えられ,その場合解は
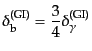 |
(L.5.268) |
となる.また
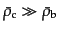 の近似のもとで,式(12.3.71)-(12.3.73)
を使い,
の近似のもとで,式(12.3.71)-(12.3.73)
を使い,
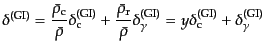 |
(L.5.269) |
を得る.ただし,各項は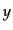 の最低次まで残した.一方,式(12.3.78)は
同じ近似で,
の最低次まで残した.一方,式(12.3.78)は
同じ近似で,
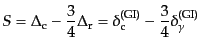 |
(L.5.270) |
となる.こうして,式(12.5.270), (12.5.274),
(12.5.275)により,
| |
|
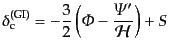 |
(L.5.271) |
| |
|
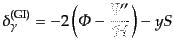 |
(L.5.272) |
が得られる.
したがって,断熱ゆらぎの場合,式(12.5.260),
(12.5.261), (12.5.273)より,
| |
|
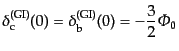 |
(L.5.273) |
| |
|
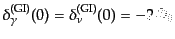 |
(L.5.274) |
となる.また等曲率ゆらぎの場合,式
(12.5.265)および(12.5.267)-(12.5.269),
(12.5.273)より,
| |
|
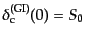 |
(L.5.275) |
| |
|
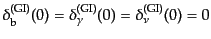 |
(L.5.276) |
| |
|
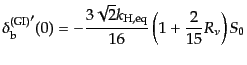 |
(L.5.277) |
| |
|
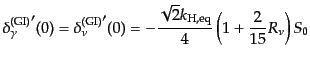 |
(L.5.278) |
が導かれる.
以上が放射優勢期に超ホライズンスケールのゆらぎがとる値であり,このゆら
ぎがホライズン内に入ってきてその後の振る舞いの初期条件となる.





次へ: 諸成分ゆらぎの進化 II: 強結合近似とゆらぎの成長
上へ: 摂動の線形成長
前へ: 宇宙の諸成分ゆらぎの発展方程式
目次
索引
All rights reserved © T.Matsubara 2004-2010
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11
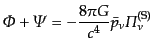
![]() の場合に0次解,
の場合に0次解,
![]() ,
,
![]() を用いて積分すれば,
を用いて積分すれば,
![]() ,
,
![]() を用いる.すると,
を用いる.すると,
![]() で全密度ゆらぎに対して
で全密度ゆらぎに対して
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11