




次へ: バリオン宇宙の困難とダークマターの必要性
上へ: 構造の形成
前へ: ジーンズ不安定性
目次
索引
Subsections
ここではまず,ジーンズ長より十分大きなスケールのゆらぎ,あるいは圧力が
無視できる物質のゆらぎに対する線形成長の解を求める.物質優勢期に入った
後,現在に至るまでのダークマターのゆらぎの線形成長はこの場合に対応し,
応用上重要なので,詳しく調べてみよう.この場合の密度ゆらぎの方程式は
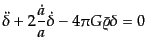 |
(F.3.34) |
である.ここで,ドットは時間微分を表している.この式は,空間微分を全く
含まず,各空間の点ごとに独立な時間の2階微分方程式になっている.すなわ
ち,ゆらぎの成長は局所的に定まってしまうのが特徴である.
はじめに,簡単なアインシュタイン・ドジッター宇宙の場合を考える.この場
合,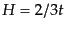 ,
,
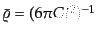 であるから,式
(6.3.34)は
であるから,式
(6.3.34)は
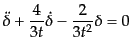 |
(F.3.35) |
となる.これは
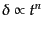 とおくことによりただちに
とおくことによりただちに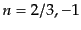 という解が見つかる.したがって一般解は
という解が見つかる.したがって一般解は
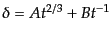 |
(F.3.36) |
である.第1項は時間とともに成長するため,成長モード(growing
mode),第2項は減衰するため,減衰モード(decaying mode)とそれぞれ
呼ばれる.減衰モードは急速に小さくなっていくので,時間がたてば無視でき
るようになる.一方,成長モードの成長はスケール因子の成長
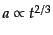 と全く同じである.したがって,物質優勢期の初期でアインシュタイ
ン・ドジッター宇宙でよく近似できるとき,十分時間がたてば
と全く同じである.したがって,物質優勢期の初期でアインシュタイ
ン・ドジッター宇宙でよく近似できるとき,十分時間がたてば
 で表される成長をすることになる.
で表される成長をすることになる.
曲率や宇宙定数の無視できないような物質優勢期以後の一般の場合の方程式
(6.3.34)も,次のようなトリックにより,解析的に求積することができ
る.まず,方程式を1階微分のない標準形に直すため,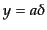 という変数
を導入すると,方程式は
という変数
を導入すると,方程式は
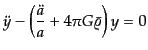 |
(F.3.37) |
となる.ここで,物質優勢のアインシュタイン方程式
からただちに
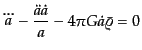 |
(F.3.40) |
となることがわかるので,うまいことに
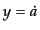 は方程式
(6.3.37)の特解になっている.2階線形微分方程式は特解が見つかれば
もう一つの解も直線的に求まる.
は方程式
(6.3.37)の特解になっている.2階線形微分方程式は特解が見つかれば
もう一つの解も直線的に求まる.
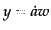 とおくと,方程式
(6.3.37)は
とおくと,方程式
(6.3.37)は
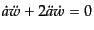 |
(F.3.41) |
となるが,これは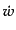 についての1階方程式であってただちに
についての1階方程式であってただちに
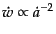 と求まり,したがって
と求まり,したがって
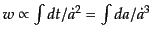 である.これで独立な2解が求まった.まとめれば,独
立解は
である.これで独立な2解が求まった.まとめれば,独
立解は
となる.ここで,物質優勢以後のハッブルパラメータ
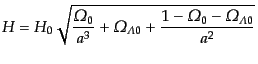 |
(F.3.44) |
を上の形に代入すればゆらぎの線形成長解の時間変化がスケール因子の関数と
して具体的に求まったことになる.アインシュタイン・ドジッター宇宙の場合
は当然ながら上で得た結果を再現する.この場合,第1の解(6.3.42)が
成長モードに対応し,第2 の解(6.3.43)が減衰モードに対応している
ことがわかる.成長モード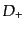 は,時間に依存する宇宙論パラメータ
は,時間に依存する宇宙論パラメータ
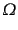 ,
,
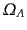 を用いて,次の便利な形に変形できる:
を用いて,次の便利な形に変形できる:
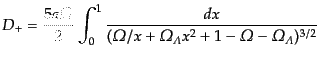 |
(F.3.45) |
ここで,比例定数は
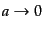 の極限で
の極限で
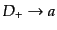 となるよ
うに選んである.
となるよ
うに選んである.
スケール因子が大きくなっていく極限では,曲率優勢の場合,
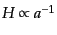 , 宇宙定数優勢の場合,
, 宇宙定数優勢の場合,
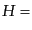 一定
となる.式
(6.3.42)の形から,曲率優勢と宇宙定数優勢の場合,ともに
一定
となる.式
(6.3.42)の形から,曲率優勢と宇宙定数優勢の場合,ともに
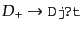 となることがわかる.これは,
膨張が速くなることによってもはやゆらぎが膨張を振り切って成長することが
できなくなるためである.
となることがわかる.これは,
膨張が速くなることによってもはやゆらぎが膨張を振り切って成長することが
できなくなるためである.
いくつかの特別な場合には,成長モードの積分の形(6.3.45)はもうすこ
し具体的に実行することができ,その結果をまとめると次のようになる.
- (a)
- アインシュタイン・ドジッター宇宙:
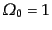 ,
,
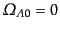
上で導いたように
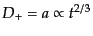 |
(F.3.46) |
- (b)
- フリードマンモデル:
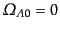
宇宙項なしの場合には,超幾何関数
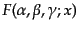 の
積分表示
の
積分表示
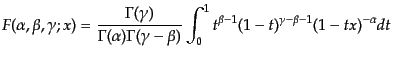 |
(F.3.47) |
により,
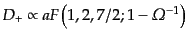 |
(F.3.48) |
となるが,さらにこれは初等積分ができ,初等関数で表せる.ここで
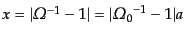 とおくと,その結果は次のよう
になる.
とおくと,その結果は次のよう
になる.
- (1)
- 開いたフリードマンモデル:
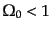
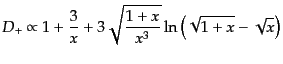 |
(F.3.49) |
- (2)
- 閉じたフリードマンモデル:
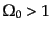
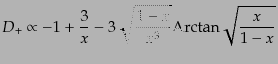 |
(F.3.50) |
ただし,これは膨張期のものである.
- (c)
- 平坦モデル:
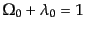
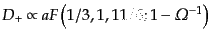 |
(F.3.51) |
上のような特別な場合以外の一般の場合には,次の近似式が便利である.
![$\displaystyle D_+ \approx \frac{5a\Omega}{2} \left[\Omega^{4/7} - \lambda + \left(1 + \frac{\Omega}{2}\right) \left(1 + \frac{\lambda}{70}\right) \right]^{-1},$](img1026.png) |
(F.3.52) |
この近似式は
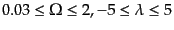 に対して,
極めてよい近似を与える.
に対して,
極めてよい近似を与える.
こうして,式(6.3.34)の一般解として,次の式が得られたことになる.
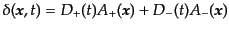 |
(F.3.53) |
ここで,
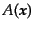 ,
,
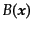 はゆらぎの初期条件によって定まる関数
である.
はゆらぎの初期条件によって定まる関数
である.
次に速度場のふるまいを線形近似の範囲内で調べてみる.そのために,連続の
式(6.1.17)を線形化すると,
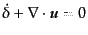 |
(F.3.54) |
となり,また,オイラー方程式(6.1.18)を線形化して回転をとると,
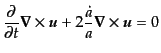 |
(F.3.55) |
となる.これらの式を見てわかるように,速度場を勾配成分と回転成分に分け
て考えると自然である
F1:
| |
|
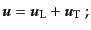 |
(F.3.56) |
| |
|
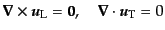 |
(F.3.57) |
この形を式(6.3.54)に入れることにより,
 |
(F.3.58) |
の勾配成分は密度ゆらぎによって表される.ここで,
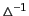 は逆ラ
プラシアン,つまりラプラシアンのグリーン関数を与える演算子である.ラプ
ラシアンは公式
は逆ラ
プラシアン,つまりラプラシアンのグリーン関数を与える演算子である.ラプ
ラシアンは公式
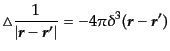 |
(F.3.59) |
を満たすので,具体的には任意の関数
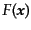 について,
について,
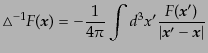 |
(F.3.60) |
である.あるいは,フーリエモード表示ではよりシンプルに
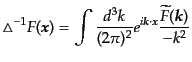 |
(F.3.61) |
であることは明らかである.ここで
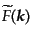 は
は
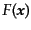 のフーリエ変換である.
のフーリエ変換である.
また,式(6.3.55)からは,
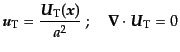 |
(F.3.62) |
となることが導かれる.ここで,
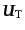 は時間的に一定の任意の
発散なしベクトル場である.速度場の回転成分は
は時間的に一定の任意の
発散なしベクトル場である.速度場の回転成分は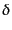 の初期条件によって
は表せないので,ここに新たに時間積分の定数である任意関数が現れてきたが,
これは減衰モードであることがわかる.すなわち,線形速度場の成長モードは
回転なしである.
の初期条件によって
は表せないので,ここに新たに時間積分の定数である任意関数が現れてきたが,
これは減衰モードであることがわかる.すなわち,線形速度場の成長モードは
回転なしである.
密度ゆらぎ(6.3.53)の2つのモードそれぞれについて,勾配成分は
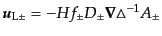 |
(F.3.63) |
となる.ここで,
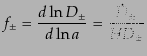 |
(F.3.64) |
を定義したが,これは式(6.3.45), (6.3.43)より具体的に
となる.この係数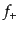 はいくつかの特別な場合には次のようになる.
はいくつかの特別な場合には次のようになる.
- (a)
- アインシュタイン・ドジッター宇宙:
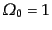 ,
,
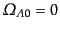
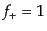 |
(F.3.67) |
- (b)
- フリードマンモデル:
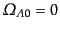
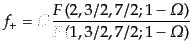 |
(F.3.68) |
これも初等関数で表せるが,その具体的な形は式(6.3.49),
(6.3.50)を微分すれば得られる.
- (c)
- 平坦モデル:
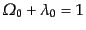
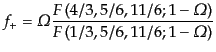 |
(F.3.69) |
ところで,成長モードについての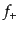 の積分の部分は
の積分の部分は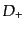 に現れてくるもの
と同じだから,近似式(6.3.52)と同じものを用いると,
に現れてくるもの
と同じだから,近似式(6.3.52)と同じものを用いると,
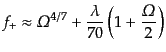 |
(F.3.70) |
という簡潔な近似式を得る.ここからわかるように,この因子の宇宙定数の値
への依存性は弱い.より大まかな
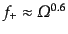 という近似式
も有名である.
という近似式
も有名である.
以上をまとめて線形速度場の形は
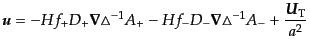 |
(F.3.71) |
となる.右辺第一項以外は減衰モードである.
初期値問題
密度ゆらぎと速度場の線形一般解が得られたので,初期条件を与えたときの形
を調べてみよう.初期時刻を
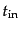 として,その時点のさまざまな変数
の値を上にinをつけて表すことにする.すなわち,初期時刻において
として,その時点のさまざまな変数
の値を上にinをつけて表すことにする.すなわち,初期時刻において
である.ふたたび
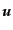 を勾配部分と回転部分に分解することにより,
を勾配部分と回転部分に分解することにより,
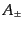 ,
,
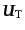 について解いて,これを一般解
(6.3.53), (6.3.71)に代入すれば,次式を得る.
について解いて,これを一般解
(6.3.53), (6.3.71)に代入すれば,次式を得る.
これが密度ゆらぎと速度場を初期値として与えたときの一般解である.ここで,
初期時刻のスケール因子が十分小さいとき,
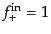 ,
,
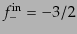 であるから,このとき上の式は
であるから,このとき上の式は
と近似できる.さらに,十分時間が経ったとき,
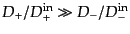 となり,さらに初期速度の回転成分
となり,さらに初期速度の回転成分
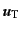 が極
端に大きくない限り
が極
端に大きくない限り
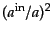 を含む項も無視できる.したがって,
上の一般解は
を含む項も無視できる.したがって,
上の一般解は
という形に近付いて行く.これが成長モードを表している.この形を見てわか
るように,初期密度ゆらぎと初期速度場が独立に与えられるならば,初期ゆら
ぎのうち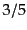 だけが成長モードになり,残りの成分は減衰モードとなって消
えて行ってしまう.そのかわりに初期速度の発散成分から密度ゆらぎの成長モー
ドが生成されてくるのである.初期密度ゆらぎがそのまま成長モードになるの
は,
だけが成長モードになり,残りの成分は減衰モードとなって消
えて行ってしまう.そのかわりに初期速度の発散成分から密度ゆらぎの成長モー
ドが生成されてくるのである.初期密度ゆらぎがそのまま成長モードになるの
は,
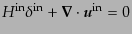 を満たすような特別な初期条件の場合のみである.線形領域にあるゆらぎは
次の「有効的な」初期ゆらぎ
を満たすような特別な初期条件の場合のみである.線形領域にあるゆらぎは
次の「有効的な」初期ゆらぎ
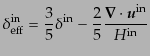 |
(F.3.80) |
が成長因子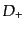 によって増幅されたものと考えることができるのである.さ
らに速度場もこの有効初期ゆらぎと独立ではなく,連続の式で関係しあってい
る.線形領域にある大きなスケールの銀河分布のゆらぎおよび速度場などの観
測により,初期ゆらぎを直接調べることが可能なのである.宇宙のより大きな
領域を調べようとする近年の観測の進歩はそれを現実的なものにしている.
によって増幅されたものと考えることができるのである.さ
らに速度場もこの有効初期ゆらぎと独立ではなく,連続の式で関係しあってい
る.線形領域にある大きなスケールの銀河分布のゆらぎおよび速度場などの観
測により,初期ゆらぎを直接調べることが可能なのである.宇宙のより大きな
領域を調べようとする近年の観測の進歩はそれを現実的なものにしている.
ジーンズ長以下のゆらぎ:音響振動
ジーンズ長より小さなスケール
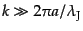 のゆらぎの成
長を考えてみる.この場合式(6.2.30)は
のゆらぎの成
長を考えてみる.この場合式(6.2.30)は
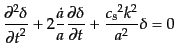 |
(F.3.81) |
となる.もし,ゆらぎの時間変化がとても速くて,宇宙膨張が無視できる場合,
フーリエ成分のゆらぎの式(6.2.30)は,
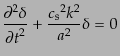 |
(F.3.82) |
となり,直ちに振動解
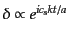 |
(F.3.83) |
を得る.これは,ゆらぎが音波として振動している状態である.波長が短くな
るほど周期は短くなる.
実際には,宇宙膨張による粘性的な効果により,この振動は減衰するはずであ
る.この効果は断熱近似(WKB近似)を用いて方程式を解くことにより見積もる
ことができる.そのために
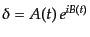 |
(F.3.84) |
とおく.ここで,振幅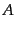 の時間変化のスケールは宇宙膨張の時間スケールと
同程度で,振動の時間スケール
の時間変化のスケールは宇宙膨張の時間スケールと
同程度で,振動の時間スケール
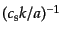 よりもずっと長いもの
とする.また
よりもずっと長いもの
とする.また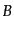 の時間変化スケールは振動の時間スケールである.式
(6.3.84)を式(6.3.81)へ代入し,その実部と虚部から
の時間変化スケールは振動の時間スケールである.式
(6.3.84)を式(6.3.81)へ代入し,その実部と虚部から
| |
|
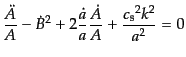 |
(F.3.85) |
| |
|
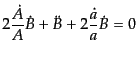 |
(F.3.86) |
の2式が得られる.ここで,小さいと仮定されている時間スケールの比の2次
のオーダーを無視するならば,第1式の第1項と第3項が無視できるので,
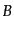 について解くことができ,
について解くことができ,
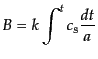 |
(F.3.87) |
が得られる.さらにこの解を第2式へ入れて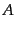 について解けば
について解けば
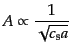 |
(F.3.88) |
となる.したがってこの近似での解のふるまいは
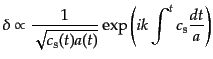 |
(F.3.89) |
となる.すなわち,宇宙膨張により,振動周期が長くなり,かつ振幅が減衰し
ていくことがわかる.
Footnotes
- ...
て考えると自然であるF1
- 一般にベクトル場は勾配成分(回転なしの成分)と回転成分(発散な
しの成分)に一意的に分解できる.上の分解で,添字のLはLongitudinal, Tは
Transverseの頭文字であるが,これはフーリエ空間でみたとき,そのベクトル
成分が波数ベクトルに平行か垂直か,を表したものである.





次へ: バリオン宇宙の困難とダークマターの必要性
上へ: 構造の形成
前へ: ジーンズ不安定性
目次
索引
All rights reserved © T.Matsubara 2004-2010
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11
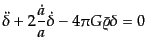
![]() ,
,
![]() であるから,式
(6.3.34)は
であるから,式
(6.3.34)は
![]() という変数
を導入すると,方程式は
という変数
を導入すると,方程式は
![]() , 宇宙定数優勢の場合,
, 宇宙定数優勢の場合,
![]() 一定
となる.式
(6.3.42)の形から,曲率優勢と宇宙定数優勢の場合,ともに
一定
となる.式
(6.3.42)の形から,曲率優勢と宇宙定数優勢の場合,ともに
![]() となることがわかる.これは,
膨張が速くなることによってもはやゆらぎが膨張を振り切って成長することが
できなくなるためである.
となることがわかる.これは,
膨張が速くなることによってもはやゆらぎが膨張を振り切って成長することが
できなくなるためである.
![]() の
積分表示
の
積分表示
![]() の積分の部分は
の積分の部分は![]() に現れてくるもの
と同じだから,近似式(6.3.52)と同じものを用いると,
に現れてくるもの
と同じだから,近似式(6.3.52)と同じものを用いると,
![]() として,その時点のさまざまな変数
の値を上にinをつけて表すことにする.すなわち,初期時刻において
として,その時点のさまざまな変数
の値を上にinをつけて表すことにする.すなわち,初期時刻において
![]() のゆらぎの成
長を考えてみる.この場合式(6.2.30)は
のゆらぎの成
長を考えてみる.この場合式(6.2.30)は
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11