




次へ: 摂動の非線形成長
上へ: 天体分布の統計理論
前へ: ゆらぎのスムージングとカウントインセル
目次
索引
Subsections
ランダムガウス場
実空間におけるランダムガウス場
2点相関関数
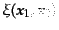 以外の高次相関関数がすべて恒等的
にゼロになるような空間的統計分布をランダムガウス場(random
Gaussian field)と呼ぶ:
以外の高次相関関数がすべて恒等的
にゼロになるような空間的統計分布をランダムガウス場(random
Gaussian field)と呼ぶ:
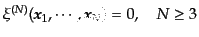 |
(O.5.106) |
ゆらぎ量
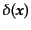 について1次のキュムラントはゼロであるから、
ランダムガウス場ではゆらぎ量について2次のキュムラント以外のキュムラン
トはすべてゼロである。このことから、ランダムガウス場のモーメントをキュ
ムラントでクラスター展開した場合、2次のキュムラント、すなわち2点相関
関数のみで表せることになる。奇数次のモーメントは2つずつクラスターにし
ていくと必ず一つ余るので、1次のキュムラントが出てきてしまい、ゼロにな
る。また、偶数次のモーメントは可能なペアの取り方だけクラスターにできる。
これらのことから、ランダムガウス場のあらゆる次数のモーメントは次のよう
になる:
について1次のキュムラントはゼロであるから、
ランダムガウス場ではゆらぎ量について2次のキュムラント以外のキュムラン
トはすべてゼロである。このことから、ランダムガウス場のモーメントをキュ
ムラントでクラスター展開した場合、2次のキュムラント、すなわち2点相関
関数のみで表せることになる。奇数次のモーメントは2つずつクラスターにし
ていくと必ず一つ余るので、1次のキュムラントが出てきてしまい、ゼロにな
る。また、偶数次のモーメントは可能なペアの取り方だけクラスターにできる。
これらのことから、ランダムガウス場のあらゆる次数のモーメントは次のよう
になる:
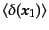 |
 |
0 |
(O.5.107) |
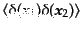 |
 |
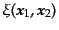 |
(O.5.108) |
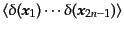 |
 |
0 |
(O.5.109) |
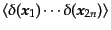 |
 |
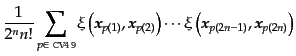 |
(O.5.110) |
ここで、最後の和は添字のあらゆる置換についての足し合わせで、あらゆる可
能なペアの取り方にくらべて重複して足しているため、その重複度で割ってあ
る。
ランダムガウス場の母汎関数は、式(15.3.68)により、
![$\displaystyle Z[J] = \exp\left[\frac12 \int d^3x_1 d^3x_2 J({\mbox{\boldmath$x$...
...x$}}_2) \xi\left({\mbox{\boldmath$x$}}_1,{\mbox{\boldmath$x$}}_2\right) \right]$](img4611.png) |
(O.5.111) |
である。これを逆ラプラス変換すれば分布汎関数![$ P[\delta]$](img4612.png) が得られるが、
無限自由度のままだと扱いにくい。そこでまず、母汎関数を離散化したものの
連続極限として、
が得られるが、
無限自由度のままだと扱いにくい。そこでまず、母汎関数を離散化したものの
連続極限として、
![$\displaystyle Z[J] = \lim \exp\left(\frac12 \sum_{i,j} \delta V_i \delta V_j J_i J_j \xi_{ij} \right)$](img4613.png) |
(O.5.112) |
と表しておこう。ここで、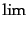 は連続極限をとることを表し、
は連続極限をとることを表し、
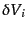 は点
は点
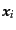 を中心とする微小体積、さらに
を中心とする微小体積、さらに
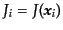 ,
,
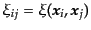 である。同じ極限において、この母
汎関数は、確率母汎関数のラプラス変換として、
である。同じ極限において、この母
汎関数は、確率母汎関数のラプラス変換として、
![$\displaystyle Z[J] = \lim \int \prod_i d\delta_i P[\delta] \exp\left(-i\sum_i \delta V_i J_i \delta_i\right)$](img4618.png) |
(O.5.113) |
と表される。これを逆ラプラス変換することで、
となる。
ここで、多次元ガウス積分の公式
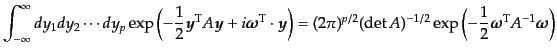 |
(O.5.115) |
によれば、空間の分割数を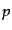 として、
として、
![$\displaystyle P[\delta] = \lim\frac{1}{(2\pi)^{p/2}\sqrt{\det(\xi_{ij})}} \exp\left[-\frac12\sum_{i,j} \delta_i \left(\xi^{-1}\right)_{ij} \delta_j\right]$](img4623.png) |
(O.5.116) |
となる。ここで、
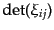 ,
,
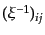 はそれぞれ
はそれぞれ
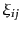 の行列式、および、逆行列の成分である。極限を取る前の形は、
多次元ガウス分布の確率分布関数に等しい。一自由度
の行列式、および、逆行列の成分である。極限を取る前の形は、
多次元ガウス分布の確率分布関数に等しい。一自由度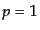 の場合、見慣れた
一自由度ガウス分布関数
の場合、見慣れた
一自由度ガウス分布関数
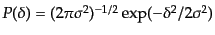 となっていることがわか
るだろう。
となっていることがわか
るだろう。
ここで、各因子の連続極限を形式的に次のように表しておく:
| |
|
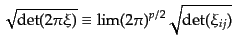 |
(O.5.117) |
| |
|
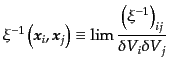 |
(O.5.118) |
ここで、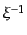 は
は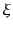 の連続的な逆行列に対応する量であり、
の連続的な逆行列に対応する量であり、
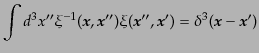 |
(O.5.119) |
を満たす。これは、
 に対応することから容易に示せる。こうして、ラン
ダムガウス場の確率母汎関数は形式的に
に対応することから容易に示せる。こうして、ラン
ダムガウス場の確率母汎関数は形式的に
![$\displaystyle P[\delta] = \frac{1}{\sqrt{(2\pi\xi)}} \exp\left[-\frac12\int d^3...
...x{\boldmath$x$}},{\mbox{\boldmath$x$}}') \delta({\mbox{\boldmath$x$}}') \right]$](img4634.png) |
(O.5.120) |
となる。
フーリエ空間におけるランダムガウス場
次に、空間的関数のゆらぎ量
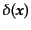 をフーリエ変換した
をフーリエ変換した
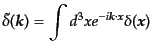 |
(O.5.121) |
がランダムガウス場についてどのような分布をするのか調べてみよう。
分布汎関数をフーリエ空間で表された変数に変換するには、確率の保存
![$\displaystyle P[\delta] \prod_{\mbox{\scriptsize\boldmath$x$}} d\delta({\mbox{...
..., \prod_{\mbox{\scriptsize\boldmath$k$}} d\tilde{\delta}({\mbox{\boldmath$k$}})$](img4636.png) |
(O.5.122) |
を用いる。すなわち、汎関数![$ P[\delta]$](img4612.png) を
を
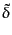 で表してから、
変換のヤコビアンを計算すれば良い。ここで、変数が無限大であるので、これ
を離散化された空間の極限として計算することになる。ただし、右辺のフーリ
エ空間の全自由度の積はシンボリックに表したもので、その具体的な意味は下
で与えられる。
で表してから、
変換のヤコビアンを計算すれば良い。ここで、変数が無限大であるので、これ
を離散化された空間の極限として計算することになる。ただし、右辺のフーリ
エ空間の全自由度の積はシンボリックに表したもので、その具体的な意味は下
で与えられる。
ここでは、統計的に空間が一様である場合を考える。この場合、統計的平均量
として与えられる関数は空間座標の並進に対して値を変えないため、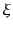 ,
,
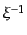 は、
は、
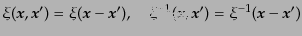 |
(O.5.123) |
という関数依存性になる。すると、式(15.5.119)はフーリエ空間におい
て、
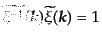 |
(O.5.124) |
という関係式となるO2。ここで、式(6.6.125)のウィーナー・ヒンチン関係により、
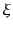 のフーリエ変換
のフーリエ変換
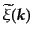 はパワースペクトル
はパワースペクトル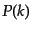 に等しい。したがって、
に等しい。したがって、
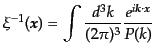 |
(O.5.125) |
であることがわかる。こうして、実空間の確率母汎関数(15.5.120)の指
数の上の積分の部分をフーリエ表示により表すと、
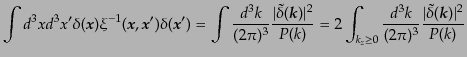 |
(O.5.126) |
となる。ここで、ゆらぎ量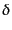 は実数であるから、そのフーリエ変換の複
素共役について、
は実数であるから、そのフーリエ変換の複
素共役について、
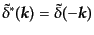 の関係にあるため、最後の積分においては
の関係にあるため、最後の積分においては
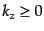 という半分の空間のみについての積分で表せることを使っている。
という半分の空間のみについての積分で表せることを使っている。
さて、実空間の時と同様、この無限自由度のままでは扱いにくい。そこで、便
宜的に、全空間を辺長 をもつ体積
をもつ体積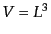 とし、周期境界条件を課すことに
より、有限化しよう。実際の空間は
とし、周期境界条件を課すことに
より、有限化しよう。実際の空間は
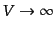 の極限を取ることに
より得られる。この有限化により、波数は
の極限を取ることに
より得られる。この有限化により、波数は
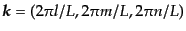 ,
,
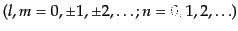 のように離散化し、
一方向あたりの波数
のように離散化し、
一方向あたりの波数 の間隔は
の間隔は
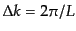 となる。以下、簡単のた
め、離散化された自由度
となる。以下、簡単のた
め、離散化された自由度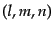 をまとめて
をまとめて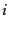 で表し、離散化した波数を
で表し、離散化した波数を
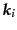 と表記する。また、離散化したフーリエ係数は便宜上
と表記する。また、離散化したフーリエ係数は便宜上
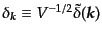 という変数で
表す。すると、確率母汎関数の指数の部分は、
という変数で
表す。すると、確率母汎関数の指数の部分は、
| |
|
![$\displaystyle \exp\left[-\frac12 \int d^3x d^3x'
\delta({\mbox{\boldmath$x$}})...
...}({\mbox{\boldmath$k$}}_i)\vert^2}{P(\vert{\mbox{\boldmath$k$}}_i\vert)}\right]$](img4650.png) |
|
| |
|
![$\displaystyle \qquad =
\lim\prod_i
\exp\left[-\frac12
\frac{\vert\delta_{{...
...p\left[-\frac{\vert\delta_{\mbox{\scriptsize\boldmath$k$}}\vert^2}{P(k)}\right]$](img4651.png) |
(O.5.127) |
と表せる。ここで、最後の式では、極限を形式的に表してある。分布汎関数の
残りの部分は規格化に伴う定数である。
フーリエ変換は線形変換であるから、式(15.5.122)の変換のヤコビア
ンも定数である。したがって、フーリエ係数を
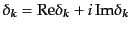 |
(O.5.128) |
のように実部と虚部に分解すれば、
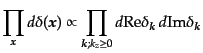 |
(O.5.129) |
となる。したがって、結局フーリエ空間の確率分布汎関数は
![$\displaystyle P[\tilde{\delta}] \prod_{\mbox{\scriptsize\boldmath$k$}} d\tild...
...x{\scriptsize\boldmath$k$}} d{\rm Im} \delta_{\mbox{\scriptsize\boldmath$k$}}$](img4654.png) |
(O.5.130) |
である。この形は、フーリエ係数
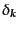 ごとに独立な積で与えら
れている。つまり、異なるフーリエモードは相互に全く独立な分布をするとい
うことである。全確率が1になるように規格化すれば、フーリエ係数の実部と
虚部も独立に分布し、その分布関数は全く同じ形で、
ごとに独立な積で与えら
れている。つまり、異なるフーリエモードは相互に全く独立な分布をするとい
うことである。全確率が1になるように規格化すれば、フーリエ係数の実部と
虚部も独立に分布し、その分布関数は全く同じ形で、
となる。
フーリエ係数の実部と虚部が独立であり、その分布関数が全く同じ形であるこ
とから、位相は全くランダムなものとなる。フーリエ係数の実部と虚部の代わ
りに、
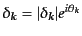 |
(O.5.133) |
により、絶対値
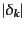 および、位相
および、位相
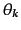 を独立変
数とする分布関数へ変換すれば、
を独立変
数とする分布関数へ変換すれば、
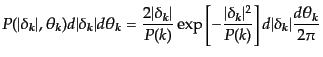 |
(O.5.134) |
となる。
このように、ランダムガウス場のフーリエ係数の位相は全くランダムに分布す
る。ことから、ランダムガウス場はランダム位相(random phase)の分布である。
ただし、この逆は真ではないことには注意する必要がある。すなわち、ランダ
ム位相の分布は必ずしもランダムガウス分布である必要はない。
Footnotes
- ...
という関係式となるO2
- ある2つの関数の畳み込みで表される関数をフー
リエ変換するとその2つの関数のフーリエ変換の積となることを容易に示すこ
とができる。この性質を畳み込みの定理(convolution theorem)と言
う。





次へ: 摂動の非線形成長
上へ: 天体分布の統計理論
前へ: ゆらぎのスムージングとカウントインセル
目次
索引
All rights reserved © T.Matsubara 2004-2010
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11
![]() 以外の高次相関関数がすべて恒等的
にゼロになるような空間的統計分布をランダムガウス場(random
Gaussian field)と呼ぶ:
以外の高次相関関数がすべて恒等的
にゼロになるような空間的統計分布をランダムガウス場(random
Gaussian field)と呼ぶ:
![]() をフーリエ変換した
をフーリエ変換した
![]() ,
,
![]() は、
は、
![]() をもつ体積
をもつ体積![]() とし、周期境界条件を課すことに
より、有限化しよう。実際の空間は
とし、周期境界条件を課すことに
より、有限化しよう。実際の空間は
![]() の極限を取ることに
より得られる。この有限化により、波数は
の極限を取ることに
より得られる。この有限化により、波数は
![]() ,
,
![]() のように離散化し、
一方向あたりの波数
のように離散化し、
一方向あたりの波数![]() の間隔は
の間隔は
![]() となる。以下、簡単のた
め、離散化された自由度
となる。以下、簡単のた
め、離散化された自由度![]() をまとめて
をまとめて![]() で表し、離散化した波数を
で表し、離散化した波数を
![]() と表記する。また、離散化したフーリエ係数は便宜上
と表記する。また、離散化したフーリエ係数は便宜上
![]() という変数で
表す。すると、確率母汎関数の指数の部分は、
という変数で
表す。すると、確率母汎関数の指数の部分は、
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11