




次へ: ランダムガウス場
上へ: 天体分布の統計理論
前へ: キュムラント展開定理
目次
索引
Subsections
ゆらぎのスムージングとカウントインセル
ゆらぎのスムージング
長さの短いスケールにおける密度ゆらぎを無視して、あるスケール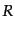 程度よ
りも長いスケールのゆらぎを取り出すことをゆらぎのスムージング、あるいは
ゆらぎの粗視化という。このスムージングの仕方は一意的ではないが、次のよ
うに密度ゆらぎをあるウィンドウ関数
程度よ
りも長いスケールのゆらぎを取り出すことをゆらぎのスムージング、あるいは
ゆらぎの粗視化という。このスムージングの仕方は一意的ではないが、次のよ
うに密度ゆらぎをあるウィンドウ関数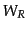 によって畳み込むことにより、ス
ムージングされた密度ゆらぎ
によって畳み込むことにより、ス
ムージングされた密度ゆらぎ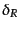 を定義する:
を定義する:
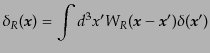 |
(O.4.79) |
このウィンドウ関数
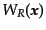 は
は
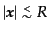 程度の領域に値を
もつような関数で、
程度の領域に値を
もつような関数で、
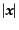 が
が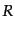 よりも十分大きなところでは実質的にゼ
ロになるようなものである。また、次の規格化の条件を満たすものとする:
よりも十分大きなところでは実質的にゼ
ロになるようなものである。また、次の規格化の条件を満たすものとする:
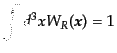 |
(O.4.80) |
もっとも良く使われるウィンドウ関数の一例は、次の球対称トップハット型:
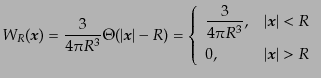 |
(O.4.81) |
である。このウィンドウ関数によれば、もとの密度ゆらぎ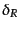 をある点
のまわり半径
をある点
のまわり半径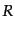 内を一様に平均した値が
内を一様に平均した値が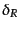 として返されることにな
る。
として返されることにな
る。
また、次のガウシアン型も良く使われるウィンドウ関数の例である:
 |
(O.4.82) |
このように、スムージングされたゆらぎに対して、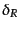 の値がどのよう
に分布するかという、一点分布関数
の値がどのよう
に分布するかという、一点分布関数
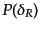 を考えてみよう。エルゴー
ト仮説により、ある固定した点での分布を考えることと、いろいろな点での値
の分布を考えることは同じなので、原点
を考えてみよう。エルゴー
ト仮説により、ある固定した点での分布を考えることと、いろいろな点での値
の分布を考えることは同じなので、原点
 における統計分
布を考えればよい。この場合のモーメント母関数を
における統計分
布を考えればよい。この場合のモーメント母関数を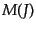 とすると、それは
とすると、それは
![$\displaystyle M(J) = \left\langle e^{-J \delta_R} \right\rangle = \left\langle...
...dmath$x$}})\right] \right\rangle = Z\left[ J W_R(-{\mbox{\boldmath$x$}})\right]$](img4560.png) |
(O.4.83) |
となり、もとの密度ゆらぎの場のモーメント母汎関数![$ Z[J]$](img4508.png) で表されることが
わかる。したがって、スムージングされたゆらぎの値のキュムラントは、
で表されることが
わかる。したがって、スムージングされたゆらぎの値のキュムラントは、
となる。つまり、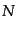 点相関関数をウィンドウ関数で平均したものに等しい。
これはもちろん、キュムラントの線形性から、式(15.4.79)からも直接
導ける。
点相関関数をウィンドウ関数で平均したものに等しい。
これはもちろん、キュムラントの線形性から、式(15.4.79)からも直接
導ける。
カウントインセル
離散的な天体分布において、ある体積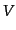 の中にある天体の数の統計を考える。
この任意に定めた体積をセルと呼ぶ。このようなセル中の天体数の分布の解析
はカウントインセル(count-in-cells)と呼ばれる。どのような形の体積
を考えるかは任意であるが、セル中に入っている天体は重みなしで数えること
にすると、これはちょうど体積内のみ一定値をとるようなウィンドウ関数で表
すことができる。このウィンドウ関数を
の中にある天体の数の統計を考える。
この任意に定めた体積をセルと呼ぶ。このようなセル中の天体数の分布の解析
はカウントインセル(count-in-cells)と呼ばれる。どのような形の体積
を考えるかは任意であるが、セル中に入っている天体は重みなしで数えること
にすると、これはちょうど体積内のみ一定値をとるようなウィンドウ関数で表
すことができる。このウィンドウ関数を
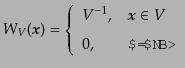 |
(O.4.85) |
と表すことにしよう。
空間を微小体積
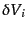 に分割してその中の天体の数を
に分割してその中の天体の数を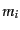 とする。こ
のとき、原点においたセル中の天体の数
とする。こ
のとき、原点においたセル中の天体の数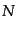 は、これは上のウィンドウ関数を
用いて
は、これは上のウィンドウ関数を
用いて
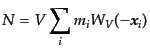 |
(O.4.86) |
となる。空間全体の数密度を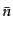 とすると、このカウント
とすると、このカウント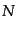 の平均は
の平均は
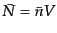 である。この数のゆらぎ
である。この数のゆらぎ
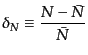 |
(O.4.87) |
は離散的な値をとる。このゆらぎは式(15.2.44)で与えられる微小体
積中の個数のゆらぎ
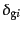 を用いて、
を用いて、
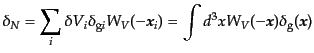 |
(O.4.88) |
と書ける。ここで、最後の式では、式(15.3.70)を用いている。
さて、こうして得られるカウントインセルの統計について、モーメント母関数
が基本的な量である。上で述べたように、モーメント母関数は統計的性質を完
全に指定し、カウントインセルにより考えられる統計量はすべてこの母関数に
帰着させられるからである。式(15.4.88)により、ある一点におけるカ
ウントのゆらぎ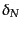 のモーメント母関数は
のモーメント母関数は
![$\displaystyle M(J) = \left\langle e^{-J \delta_N} \right\rangle = Z_{\rm g}[J W_V(-{\mbox{\boldmath$x$}})]$](img4570.png) |
(O.4.89) |
となることがわかる。すると、式(15.4.85)のようにセルの中で一定値
をとるというウィンドウ関数の性質を使えば、離散分布の母汎関数の表式
(15.3.75)により、
![$\displaystyle M(J) = e^J \left\langle \exp\left[\left(e^{-J/\bar{N}}-1\right) V...
...d^3x W_V(-{\mbox{\boldmath$x$}}) n({\mbox{\boldmath$x$}}) \right] \right\rangle$](img4571.png) |
(O.4.90) |
となる。ここでさらにキュムラント展開定理を適用すると、
![$\displaystyle M(J) = e^J \exp\left[\bar{N} \left(e^{-J/\bar{N}} - 1\right) + \s...
...\right)^k \left(e^{-J/\bar{N}} - 1\right)^k}{k!} \overline{\xi}^{(k)}_V \right]$](img4572.png) |
(O.4.91) |
となる。ここで、
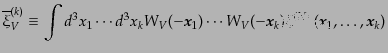 |
(O.4.92) |
であり、また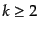 の場合
の場合
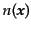 の
の 次のキュムラントは
次のキュムラントは
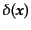 の
の 次のキュムラントの
次のキュムラントの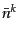 倍であることを用い
ている。
倍であることを用い
ている。
カウントのゆらぎのキュムラントは
となる。これは式(15.4.91)の対数を微分することにより、密度場の相
関関数で表すことができる。もちろん、式(15.2.46),
(15.2.47)のような式を積分することによっても同じ式が導ける。最初
のいくつかは
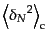 |
 |
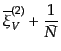 |
(O.4.94) |
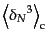 |
 |
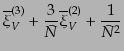 |
(O.4.95) |
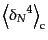 |
 |
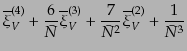 |
(O.4.96) |
などとなる。
セル中のカウントが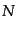 となる確率を
となる確率を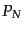 とすると、このカウントの確率分布
そのものを与えるような母関数
とすると、このカウントの確率分布
そのものを与えるような母関数
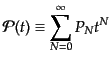 |
(O.4.97) |
を考えることもある。このとき、カウントの確率分布は
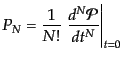 |
(O.4.98) |
で与えられる。このカウントの母関数は上で求めた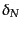 の母関数により
次のように求められる:
の母関数により
次のように求められる:
これを使えば、カウント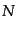 のモーメントは
のモーメントは
 |
(O.4.100) |
と表せて、さらにキュムラントは
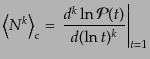 |
(O.4.101) |
となる。
ボイド確率関数
体積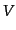 中に一つも天体が入らない確率
中に一つも天体が入らない確率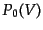 を特にボイド確率関数と呼び、
次式で与えられる:
を特にボイド確率関数と呼び、
次式で与えられる:
![$\displaystyle P_0(V) = {\cal P}(0) = \left\langle \exp\left[-V\int d^3x W_V(-{\...
...ar{N} + \sum_{N=0}^\infty \frac{(-\bar{N})^N}{N!} \overline{\xi}^{(N)}_V\right]$](img4595.png) |
(O.4.102) |
この式からただちに、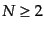 に対して
に対して
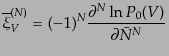 |
(O.4.103) |
となることがわかる。
ここで、式(15.4.99)において、
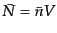 であることから
であることから
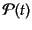 が
が
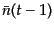 の関数であることに着目すると、
の関数であることに着目すると、
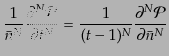 |
(O.4.104) |
である。この両辺を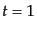 で評価することにより、
で評価することにより、
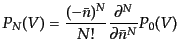 |
(O.4.105) |
という式が導かれる。したがって、ボイド確率関数は平均数密度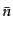 を
変化させるとき
を
変化させるとき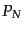 の母関数となっている。
の母関数となっている。





次へ: ランダムガウス場
上へ: 天体分布の統計理論
前へ: キュムラント展開定理
目次
索引
All rights reserved © T.Matsubara 2004-2010
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11
![]() 程度よ
りも長いスケールのゆらぎを取り出すことをゆらぎのスムージング、あるいは
ゆらぎの粗視化という。このスムージングの仕方は一意的ではないが、次のよ
うに密度ゆらぎをあるウィンドウ関数
程度よ
りも長いスケールのゆらぎを取り出すことをゆらぎのスムージング、あるいは
ゆらぎの粗視化という。このスムージングの仕方は一意的ではないが、次のよ
うに密度ゆらぎをあるウィンドウ関数![]() によって畳み込むことにより、ス
ムージングされた密度ゆらぎ
によって畳み込むことにより、ス
ムージングされた密度ゆらぎ![]() を定義する:
を定義する:
![]() の値がどのよう
に分布するかという、一点分布関数
の値がどのよう
に分布するかという、一点分布関数
![]() を考えてみよう。エルゴー
ト仮説により、ある固定した点での分布を考えることと、いろいろな点での値
の分布を考えることは同じなので、原点
を考えてみよう。エルゴー
ト仮説により、ある固定した点での分布を考えることと、いろいろな点での値
の分布を考えることは同じなので、原点
![]() における統計分
布を考えればよい。この場合のモーメント母関数を
における統計分
布を考えればよい。この場合のモーメント母関数を![]() とすると、それは
とすると、それは
![]() の中にある天体の数の統計を考える。
この任意に定めた体積をセルと呼ぶ。このようなセル中の天体数の分布の解析
はカウントインセル(count-in-cells)と呼ばれる。どのような形の体積
を考えるかは任意であるが、セル中に入っている天体は重みなしで数えること
にすると、これはちょうど体積内のみ一定値をとるようなウィンドウ関数で表
すことができる。このウィンドウ関数を
の中にある天体の数の統計を考える。
この任意に定めた体積をセルと呼ぶ。このようなセル中の天体数の分布の解析
はカウントインセル(count-in-cells)と呼ばれる。どのような形の体積
を考えるかは任意であるが、セル中に入っている天体は重みなしで数えること
にすると、これはちょうど体積内のみ一定値をとるようなウィンドウ関数で表
すことができる。このウィンドウ関数を
![]() に分割してその中の天体の数を
に分割してその中の天体の数を![]() とする。こ
のとき、原点においたセル中の天体の数
とする。こ
のとき、原点においたセル中の天体の数![]() は、これは上のウィンドウ関数を
用いて
は、これは上のウィンドウ関数を
用いて
![]() のモーメント母関数は
のモーメント母関数は
![]() となる確率を
となる確率を![]() とすると、このカウントの確率分布
そのものを与えるような母関数
とすると、このカウントの確率分布
そのものを与えるような母関数
![]() 中に一つも天体が入らない確率
中に一つも天体が入らない確率![]() を特にボイド確率関数と呼び、
次式で与えられる:
を特にボイド確率関数と呼び、
次式で与えられる:
![]() であることから
であることから
![]() が
が
![]() の関数であることに着目すると、
の関数であることに着目すると、
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11