




次へ: 宇宙の優勢成分のゆらぎ
上へ: 摂動の線形成長
前へ: 摂動の線形成長
目次
索引
ゆらぎの成長はスケールごとに異なっているので,ゆらぎをスケールごとにモー
ド分解すると便利である.平坦な空間では大局的に直交デカルト座標を張れる
ので,その場合には基底
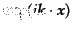 によって平面波展開を
すればよく,
によって平面波展開を
すればよく,
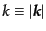 によりゆらぎのスケールが特徴づけられる.
だが,宇宙の曲率が無視できないスケールを考える場合にはこの分解は使えな
い.一般の定曲率空間におけるモード分解にはラプラシアン
によりゆらぎのスケールが特徴づけられる.
だが,宇宙の曲率が無視できないスケールを考える場合にはこの分解は使えな
い.一般の定曲率空間におけるモード分解にはラプラシアン
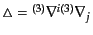 の固有関数により完全系をなす基底を構
成するとよい.もちろん,平坦な空間の平面波展開はこれを満たしていて波数
の固有関数により完全系をなす基底を構
成するとよい.もちろん,平坦な空間の平面波展開はこれを満たしていて波数
 のモードの固有値は
のモードの固有値は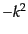 である.一般の場合のモード関数の固有値もゆ
らぎのスケールを特徴づけるものであり,その固有値を
である.一般の場合のモード関数の固有値もゆ
らぎのスケールを特徴づけるものであり,その固有値を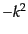 で特徴づける.
で特徴づける.
そこで,モード関数の定義として,スカラー型のゆらぎについて
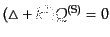 |
(L.1.1) |
ベクトル型のゆらぎについて
テンソル型のゆらぎについて
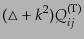 |
 |
0 |
(L.1.4) |
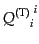 |
 |
0 |
(L.1.5) |
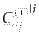 |
 |
0 |
(L.1.6) |
という方程式を使う.ベクトル型,テンソル型は複数の条件が課されるが,こ
れらは定曲率空間の場合には無矛盾である.このことはベクトルやテンソルに
作用したときのラプラシアンと共変微分の交換関係を,定曲率空間の3次元曲
率テンソルを使って導くことにより示すことができる.
定曲率空間の対称性のため,これらの固有関数は について縮退した独立な
解から構成される.例えば平坦な空間におけるスカラー型のゆらぎでは,平面
波展開の基底
について縮退した独立な
解から構成される.例えば平坦な空間におけるスカラー型のゆらぎでは,平面
波展開の基底
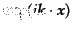 も,フーリエ・ベッセル展開の基
底
も,フーリエ・ベッセル展開の基
底
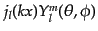 も固有値
も固有値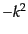 に属するラプラシアンの固有
関数である.縮退した自由度については自由に基底を選べるが,それをどのよ
うに選ぶのが自然かは,背景の定曲率空間に張った座標系の具体的な形による.
例として,定曲率空間の球座標表示の場合に具体的にスカラー型の固有関数を
見てみよう.計量は式(10.2.2)で与えられる次の形
に属するラプラシアンの固有
関数である.縮退した自由度については自由に基底を選べるが,それをどのよ
うに選ぶのが自然かは,背景の定曲率空間に張った座標系の具体的な形による.
例として,定曲率空間の球座標表示の場合に具体的にスカラー型の固有関数を
見てみよう.計量は式(10.2.2)で与えられる次の形
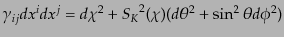 |
(L.1.7) |
である.スカラー関数のラプラシアンは式(B.2.49)に類似の公式
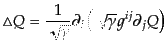 |
(L.1.8) |
で与えられるので,式(12.1.1)はただちに
![$\displaystyle \frac{1}{{{S_K}}^2(\chi)} \left[ \frac{\partial}{\partial\chi} \l...
...+ \frac{1}{\sin^2\theta}\frac{\partial^2 Q}{\partial\phi^2} \right] + k^2 Q = 0$](img3682.png) |
(L.1.9) |
となることがわかる.ここで変数分離法によれば,角方向には球面調和関数で
分離され,
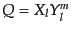 の形となる.ここで,動径方向の関数
の形となる.ここで,動径方向の関数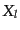 は次の
微分方程式を満たす:
は次の
微分方程式を満たす:
![$\displaystyle \frac{1}{{S_K}^2(\chi)} \frac{\partial}{\partial\chi} \left( {S_K...
...artial\chi} \right) + \left[ k^2 - \frac{l(l+1)}{{S_K}^2(\chi)} \right] X_l = 0$](img3685.png) |
(L.1.10) |
この方程式は
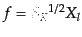 ,
,
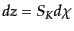 とおくとルジャンドル陪微分方程式に帰着し,原点
で正則な解をとればよい.その解は,曲率が負,ゼロ,正のときそれぞれ,円
錐関数(conical function),ベッセル関数,円環関数(toroidal function)と
して知られる関数で表される.これは
とおくとルジャンドル陪微分方程式に帰着し,原点
で正則な解をとればよい.その解は,曲率が負,ゼロ,正のときそれぞれ,円
錐関数(conical function),ベッセル関数,円環関数(toroidal function)と
して知られる関数で表される.これは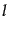 が整数のとき初等関数で表されるあ
らわな形となり,まとめて
が整数のとき初等関数で表されるあ
らわな形となり,まとめて
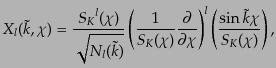 |
(L.1.11) |
というシンプルな形となる.ここで,
 ,また,
,また,
 は任意の規格化因子である.規格化因子を別にすれば,この解の
は任意の規格化因子である.規格化因子を別にすれば,この解の 依存性は
依存性は
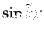 ,
,
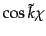 で与えられるが,このことから類推されるように,曲率がゼロ
または負のとき基底が2乗可積分となるためにスペクトルのとり得る範囲は
で与えられるが,このことから類推されるように,曲率がゼロ
または負のとき基底が2乗可積分となるためにスペクトルのとり得る範囲は
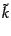 が実数,すなわち
が実数,すなわち
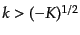 である.一方,曲率が正のと
きは有限体積であるから,
である.一方,曲率が正のと
きは有限体積であるから,
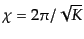 で空間が周期的になってい
て,
で空間が周期的になってい
て,
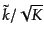 は正の整数でなければならない.ただし,
は正の整数でなければならない.ただし,
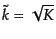 の場合は
の場合は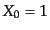 ,
,
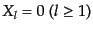 という一
様解を与えるので,結局,
という一
様解を与えるので,結局,
 である.
このような離散的な
である.
このような離散的な の場合,式(12.1.11)で与えられる関数は
Gegenbauerの多項式で表され,
の場合,式(12.1.11)で与えられる関数は
Gegenbauerの多項式で表され,
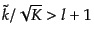 である.
である.
規格化因子として,
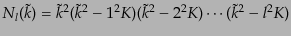 |
(L.1.12) |
と選ぶと,基底の直交関係,完全性関係が比較的簡潔になる.実際,曲率がゼ
ロまたは負の場合
 ,円錐関数, ベッセル関数の直交関係および
完全性関係から,
,円錐関数, ベッセル関数の直交関係および
完全性関係から,
| |
|
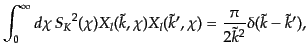 |
(L.1.13) |
| |
|
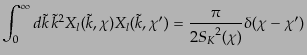 |
(L.1.14) |
また,曲率が正の場合 ,Gegenbauer多項式の直交関係および完全性
関係から,
,Gegenbauer多項式の直交関係および完全性
関係から,
| |
|
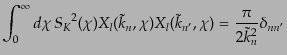 |
(L.1.15) |
| |
|
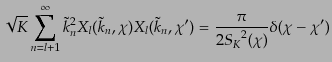 |
(L.1.16) |
という関係が導かれる.ここで,
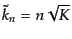 は正定曲率空間の離散的スペ
クトルである.
は正定曲率空間の離散的スペ
クトルである.
共動距離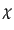 に関する微分は式(12.1.11)を直接微分して,
に関する微分は式(12.1.11)を直接微分して,
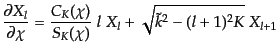 |
(L.1.17) |
となる.ここで,
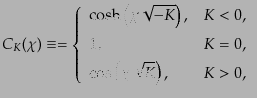 |
|
|
(L.1.18) |
を用いた.この関数には
| |
|
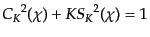 |
(L.1.19) |
| |
|
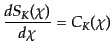 |
(L.1.20) |
| |
|
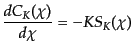 |
(L.1.21) |
という性質がある.式(12.1.17)を微分方程式(12.1.10)へ代入すれ
ば,再帰的関係
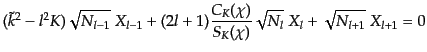 |
(L.1.22) |
を得る.さらに式(12.1.17), (12.1.22)より,次の有用な式が得ら
れる.
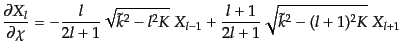 |
(L.1.23) |
具体的に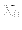 および
および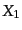 の形を式(12.1.11)から求めれば,高次の形は
再帰的関係式(12.1.22)により導き出すことができる.その結果,最初の
5つの具体的な形は次のようになる:
の形を式(12.1.11)から求めれば,高次の形は
再帰的関係式(12.1.22)により導き出すことができる.その結果,最初の
5つの具体的な形は次のようになる:
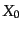 |
 |
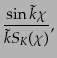 |
(L.1.24) |
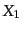 |
 |
![$\displaystyle \frac{1}{\sqrt{N_1(\tilde{k})}\; {S_K}^2(\chi)}
\left[ - {C_K}(\chi)\sin \tilde{k}\chi
+ \tilde{k} {S_K}(\chi)\cos \tilde{k}\chi\right],$](img3723.png) |
(L.1.25) |
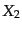 |
 |
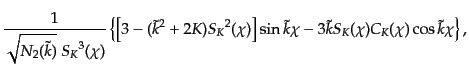 |
(L.1.26) |
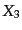 |
 |
![$\displaystyle \frac{1}{\sqrt{N_3(\tilde{k})}\; {S_K}^4(\chi)}
\left\{
{C_K}(\...
... - 15 + 6 (\tilde{k}^2 + K) {S_K}^2(\chi)
\right]
\sin \tilde{k}\chi
\right.$](img3727.png) |
|
| |
|
![$\displaystyle \qquad\qquad\qquad\qquad\qquad +
\left.
\tilde{k}{S_K}(\chi)
...
... 15 - (\tilde{k}^2 + 11K) {S_K}^2(\chi)
\right]
\cos \tilde{k}\chi
\right\},$](img3728.png) |
(L.1.27) |
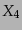 |
 |
![$\displaystyle \frac{1}{\sqrt{N_4(\tilde{k})}{S_K}^5(\chi)}
\left\{
\left[
10...
... + 35K \tilde{k}^2 + 24K^2) {S_K}^4(\chi)
\right]
\sin \tilde{k}\chi
\right.$](img3730.png) |
|
| |
|
![$\displaystyle \qquad\qquad\qquad\qquad -
\left.
\tilde{k} {S_K}(\chi)
\lef...
...05 - 10(\tilde{k}^2 + 5K) {S_K}^2(\chi)
\right]
\cos \tilde{k}\chi
\right\},$](img3731.png) |
(L.1.28) |
平坦な空間 の場合には確かに
の場合には確かに
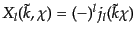 と,ベッセル関数になっている.
と,ベッセル関数になっている.
ベクトル型,テンソル型のモード関数も条件(12.1.2)-(12.1.6)
をこの座標系で具体的に書き下して解いて行くことが可能である.その結果は
ベクトル調和関数やテンソル調和関数,あるいはスピン調和関数を使って表示
できるが,それらは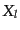 ,
, 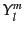 およびその座標微分のみで表すこ
とができるようなものである.
およびその座標微分のみで表すこ
とができるようなものである.
こうして,任意の空間的関数
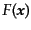 は完全系をなすモード
は完全系をなすモード
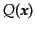 の重ね合わせとして表現できる.たとえばスカラー関数を上で述べた球座標に
おけるモードで分解すると,
の重ね合わせとして表現できる.たとえばスカラー関数を上で述べた球座標に
おけるモードで分解すると, の場合,
の場合,
また,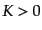 の場合,
の場合,
となる.ただし,後者の場合は
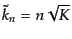 ,
, 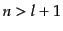 であ
る.このような分解により,ラプラシアンは
であ
る.このような分解により,ラプラシアンは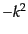 に置き換わり,
運動方程式は変数の各モードについて全く独立なものに分解してしまう.例え
ば、スカラー成分についてのバーディーン変数による運動方程式
(10.4.166)-(10.4.169)はモードの成分ごとに,
に置き換わり,
運動方程式は変数の各モードについて全く独立なものに分解してしまう.例え
ば、スカラー成分についてのバーディーン変数による運動方程式
(10.4.166)-(10.4.169)はモードの成分ごとに,
| |
|
![$\displaystyle \Delta' - 3 w {\cal H}\Delta
= \left(k^2 - 3K \right)
\left[ (1 + w) V - 2 w {\cal H}{\mit\Pi}\right]$](img3743.png) |
(L.1.33) |
| |
|
![$\displaystyle V' + {\cal H}V
= - \frac{{c_s}^2}{1 + w} \Delta - \Phi
- \frac{w}{1+w}
\left[
\Gamma - \frac23 (k^2 - 3K) {\mit\Pi}
\right]$](img3744.png) |
(L.1.34) |
| |
|
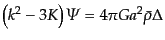 |
(L.1.35) |
| |
|
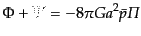 |
(L.1.36) |
である.ここで,混乱のおそれのない限り,スカラー成分を表す記号(S)を省
略する.各変数はいまや空間座標の関数ではなく,モードのラベル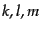 と
時間の関数であるが,これらのラベルも省略してある.
と
時間の関数であるが,これらのラベルも省略してある.





次へ: 宇宙の優勢成分のゆらぎ
上へ: 摂動の線形成長
前へ: 摂動の線形成長
目次
索引
All rights reserved © T.Matsubara 2004-2010
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11
![]() によって平面波展開を
すればよく,
によって平面波展開を
すればよく,
![]() によりゆらぎのスケールが特徴づけられる.
だが,宇宙の曲率が無視できないスケールを考える場合にはこの分解は使えな
い.一般の定曲率空間におけるモード分解にはラプラシアン
によりゆらぎのスケールが特徴づけられる.
だが,宇宙の曲率が無視できないスケールを考える場合にはこの分解は使えな
い.一般の定曲率空間におけるモード分解にはラプラシアン
![]() の固有関数により完全系をなす基底を構
成するとよい.もちろん,平坦な空間の平面波展開はこれを満たしていて波数
の固有関数により完全系をなす基底を構
成するとよい.もちろん,平坦な空間の平面波展開はこれを満たしていて波数
![]() のモードの固有値は
のモードの固有値は![]() である.一般の場合のモード関数の固有値もゆ
らぎのスケールを特徴づけるものであり,その固有値を
である.一般の場合のモード関数の固有値もゆ
らぎのスケールを特徴づけるものであり,その固有値を![]() で特徴づける.
で特徴づける.
![]() について縮退した独立な
解から構成される.例えば平坦な空間におけるスカラー型のゆらぎでは,平面
波展開の基底
について縮退した独立な
解から構成される.例えば平坦な空間におけるスカラー型のゆらぎでは,平面
波展開の基底
![]() も,フーリエ・ベッセル展開の基
底
も,フーリエ・ベッセル展開の基
底
![]() も固有値
も固有値![]() に属するラプラシアンの固有
関数である.縮退した自由度については自由に基底を選べるが,それをどのよ
うに選ぶのが自然かは,背景の定曲率空間に張った座標系の具体的な形による.
例として,定曲率空間の球座標表示の場合に具体的にスカラー型の固有関数を
見てみよう.計量は式(10.2.2)で与えられる次の形
に属するラプラシアンの固有
関数である.縮退した自由度については自由に基底を選べるが,それをどのよ
うに選ぶのが自然かは,背景の定曲率空間に張った座標系の具体的な形による.
例として,定曲率空間の球座標表示の場合に具体的にスカラー型の固有関数を
見てみよう.計量は式(10.2.2)で与えられる次の形
![]() に関する微分は式(12.1.11)を直接微分して,
に関する微分は式(12.1.11)を直接微分して,
![]() ,
, ![]() およびその座標微分のみで表すこ
とができるようなものである.
およびその座標微分のみで表すこ
とができるようなものである.
![]() は完全系をなすモード
は完全系をなすモード
![]() の重ね合わせとして表現できる.たとえばスカラー関数を上で述べた球座標に
おけるモードで分解すると,
の重ね合わせとして表現できる.たとえばスカラー関数を上で述べた球座標に
おけるモードで分解すると,![]() の場合,
の場合,
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11