




次へ: 密度ゆらぎの相関関数とパワースペクトル
上へ: 構造の形成
前へ: バリオン宇宙の困難とダークマターの必要性
目次
索引
Subsections
ダークマターの存在を仮定して,輻射優勢期から物質優勢期に移り変わる時期
のダークマターのゆらぎの成長を調べてみよう.この時期にはあらゆるスケー
ルでゆらぎは十分小さいので,線形理論が極めてよい近似である.また,ダー
クマターはその定義によって圧力が無視できるものである.したがって,式
(6.1.23) を線形化したものを輻射とダークマターの混在する場合につ
いて考えればよい:
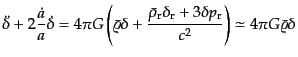 |
(F.5.97) |
輻射のゆらぎ
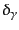 ,
,
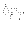 はここまでのニュートン近
似の枠内では正確に与えられないが,この時期の輻射のジーンズ長はホライズ
ンスケールである.そこで,ニュートン近似の使えるようなホライズンスケー
ルより十分小さいスケールでは,近似的に輻射はゆらいでいないものと仮定し
て
はここまでのニュートン近
似の枠内では正確に与えられないが,この時期の輻射のジーンズ長はホライズ
ンスケールである.そこで,ニュートン近似の使えるようなホライズンスケー
ルより十分小さいスケールでは,近似的に輻射はゆらいでいないものと仮定し
て
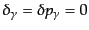 とおいたのが上の式の右辺の近似
式である.いま考えている時期では宇宙項も曲率も無視できるので
とおいたのが上の式の右辺の近似
式である.いま考えている時期では宇宙項も曲率も無視できるので
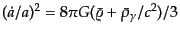 とな
ることを使い,また,時間
とな
ることを使い,また,時間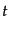 のかわりに変数
のかわりに変数
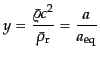 |
(F.5.98) |
を導入すれば,方程式は
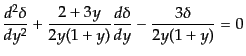 |
(F.5.99) |
となる.この方程式は超幾何微分方程式であるが,上の場合は縮退した方程式
といわれるもので,一方の解は単なる多項式になる.もう一方の解も初等関数
で表される.その結果,成長モードは
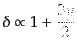 |
(F.5.100) |
となり,また減衰モードは
![$\displaystyle \delta \propto \left(1 + \frac{3y}{2}\right) \ln\left[\frac{\sqrt{1+y} + 1}{\sqrt{1+y} - 1}\right] -3\sqrt{1+y}$](img1127.png) |
(F.5.101) |
となる.減衰モードはいまは考えない.ここからすぐわかることは,輻射優勢
期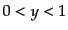 にはほとんどダークマターのゆらぎが成長できないことである.実
際,この間の成長モードは
にはほとんどダークマターのゆらぎが成長できないことである.実
際,この間の成長モードは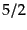 倍にしかならない.これは輻射優勢期では宇
宙の膨張速度がダークマターのゆらぎの成長速度に比べて速すぎるためにゆら
ぎの成長が実質的に止まってしまうことを意味している.
物質優勢期に入るとこの成長モードは上で調べたアインシュタイン
ドジッター宇宙のゆらぎの成長則
倍にしかならない.これは輻射優勢期では宇
宙の膨張速度がダークマターのゆらぎの成長速度に比べて速すぎるためにゆら
ぎの成長が実質的に止まってしまうことを意味している.
物質優勢期に入るとこの成長モードは上で調べたアインシュタイン
ドジッター宇宙のゆらぎの成長則
 に徐々に従うようになる.
このような輻射優勢期でのゆらぎの成長の停滞現象をMészáros効果
と呼ぶ.
に徐々に従うようになる.
このような輻射優勢期でのゆらぎの成長の停滞現象をMészáros効果
と呼ぶ.
物質優勢期に入ってから,宇宙の晴れ上がりまで,バリオンのゆらぎは輻射と
強く結合しているために成長できず,これがバリオンでできた宇宙の困難になっ
ていた.一方でダークマターにはそのような結合がないため,
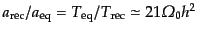 の因
子だけ成長できる.宇宙が晴れ上がった後のバリオンはダークマターのつくる
ポテンシャルの中に落ち込むことによりゆらぎの成長が進む.このプロセスを
調べてみる.まず,ダークマターとバリオンの混合系におけるバリオンゆらぎ
の因
子だけ成長できる.宇宙が晴れ上がった後のバリオンはダークマターのつくる
ポテンシャルの中に落ち込むことによりゆらぎの成長が進む.このプロセスを
調べてみる.まず,ダークマターとバリオンの混合系におけるバリオンゆらぎ
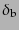 の線形成長は式(6.1.23)から
の線形成長は式(6.1.23)から
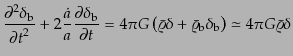 |
(F.5.102) |
で記述される.ここで,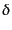 はダークマターのゆらぎであり,バリオンが
ダークマターに比べて無視できるとしたのが右辺の近似式である.ここで,時
間
はダークマターのゆらぎであり,バリオンが
ダークマターに比べて無視できるとしたのが右辺の近似式である.ここで,時
間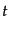 のかわりに変数
のかわりに変数
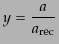 |
(F.5.103) |
を導入すれば,方程式は
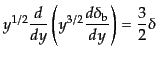 |
(F.5.104) |
となるが,いまの近似では
 であるので,これは容易に解け
る.晴れ上がりのときにはバリオンが全くゆらいでいないとして,
であるので,これは容易に解け
る.晴れ上がりのときにはバリオンが全くゆらいでいないとして,
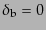 という初期条件による解は
という初期条件による解は
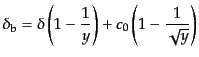 |
(F.5.105) |
となる.速度についての初期条件を与えていないので,積分定数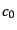 が残っ
ているが,いずれにしても晴れ上がり以後
が残っ
ているが,いずれにしても晴れ上がり以後
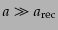 となるにつれ
てバリオンのゆらぎはダークマターのゆらぎに等しくなってゆくことがわかる.
このことはバリオンゆらぎの追いつき現象と呼ばれている.
となるにつれ
てバリオンのゆらぎはダークマターのゆらぎに等しくなってゆくことがわかる.
このことはバリオンゆらぎの追いつき現象と呼ばれている.
ダークマターは(定義によって)重力以外の相互作用をしない無衝突粒子であ
る.するとその速度分散によっては粒子の自由運動 (free streaming) によっ
てゆらぎが減衰してしまうことになる.これを無衝突減衰
(collisionless damping)という.無衝突減衰がどの程度起こるかは,粒子の
速度分散がどのくらいかで決まる.そこで粒子の典型的な速度の時間変化を
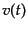 とすると,時間間隔
とすると,時間間隔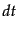 の間に共動距離
の間に共動距離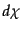 走るならば,
走るならば,
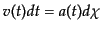 である.したがって粒子の自由運動のスケールは共動距離にして
である.したがって粒子の自由運動のスケールは共動距離にして
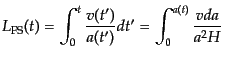 |
(F.5.106) |
である.ここで粒子が相対論的でなくなる時期のスケール因子を
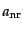 とすると,式(4.3.42)から
とすると,式(4.3.42)から
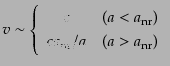 |
(F.5.107) |
となる.ここでもし
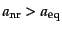 であると、自由運動が大きす
ぎて十分な構造を形成することができなくなってしまうので,ここでは粒子は
等密度時までには非相対論的になっている
であると、自由運動が大きす
ぎて十分な構造を形成することができなくなってしまうので,ここでは粒子は
等密度時までには非相対論的になっている
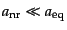 とし
よう.積分(6.5.106)を
とし
よう.積分(6.5.106)を
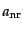 ,
,
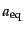 を境として分けら
れる3つの時期に分け、輻射優勢期と物質優勢期のハッブルパラメータ
を境として分けら
れる3つの時期に分け、輻射優勢期と物質優勢期のハッブルパラメータ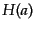 の漸近形
の漸近形
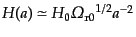 (RD),
(RD),
 (MD)をそれぞれ用いる近似
で計算すると、
(MD)をそれぞれ用いる近似
で計算すると、
となる。ここで、
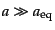 となるときに上式は一定の値
となるときに上式は一定の値
![$\displaystyle L_{\rm FS}(t) \simeq \frac{c a_{\rm nr}}{H_0 \sqrt{{\mit\Omega}_{\rm r0}}} \left[ 3 + \ln\left(\frac{a_{\rm eq}}{a_{\rm nr}}\right) \right]$](img1154.png) |
(F.5.109) |
に近付く。こうして,ダークマターが非相対論的になる時期
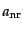 によっ
てこのスケールが決まる.ダークマターとなる粒子の質量が重くて十分早い時
期に非相対論的になる場合は,
によっ
てこのスケールが決まる.ダークマターとなる粒子の質量が重くて十分早い時
期に非相対論的になる場合は,
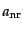 が十分小さくなり、減衰スケール
は十分小さく,無衝突減衰はあまり効かないことになる.逆に粒子の質量が小
さく,
が十分小さくなり、減衰スケール
は十分小さく,無衝突減衰はあまり効かないことになる.逆に粒子の質量が小
さく,
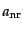 が大きければ無衝突減衰が大きいスケールまで効くことに
なる.
が大きければ無衝突減衰が大きいスケールまで効くことに
なる.
ダークマターの質量を
 とするとき、無衝突減衰のスケールを求め
てみよう。ダークマターが非相対論的になる温度は
とするとき、無衝突減衰のスケールを求め
てみよう。ダークマターが非相対論的になる温度は
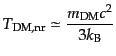 |
(F.5.110) |
と見積もれるが、このときダークマターはすでに脱結合しているかもしれず、
この温度はそのときの光子の温度
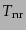 とは等しくない。ダークマター
が相対論的である時期には、
とは等しくない。ダークマター
が相対論的である時期には、
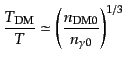 |
(F.5.111) |
である。ただし、簡単のため、有効自由度の変化による光子のエントロピー増
加による温度変化は無視している。ここで、ダークマターの現在の数密度は、
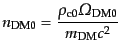 |
(F.5.112) |
である。ダークマターが非相対論的になるときの温度についても、式
(6.5.111)の比が近似的に成り立っているとすると、これらの式によ
り
となる.したがって,無衝突減衰のスケールは結局
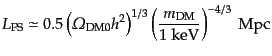 |
(F.5.114) |
となる.
ダークマターの詳細は構造形成にあまり影響しないが,上のように無衝突減衰
のスケールを決める
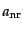 の値は構造形成に多大な影響がある.そこで,
ダークマターは大きく2種類に分けられることになる.一つは無衝突減衰の影
響の大きいホットダークマター (Hot dark matter; HDM)であり,もう
一つは無衝突減衰のほとんど効かないコールドダー
クマター (Cold dark matter; CDM)である.
の値は構造形成に多大な影響がある.そこで,
ダークマターは大きく2種類に分けられることになる.一つは無衝突減衰の影
響の大きいホットダークマター (Hot dark matter; HDM)であり,もう
一つは無衝突減衰のほとんど効かないコールドダー
クマター (Cold dark matter; CDM)である.
ホットダークマターは等密度時までに自由運動によって小さなスケールのゆら
ぎがならされてしまっている.したがってその時点まで速度分散が大きかった
ためにホットという名前がついている.ホットダークマターの典型的な例は質
量を持つニュートリノである.ニュートリノがダークマターとして宇宙の質量
を担っているならば,式(4.4.56)により、
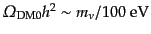 となるので、自由運動の共動スケールおよびその質量ス
ケールは
となるので、自由運動の共動スケールおよびその質量ス
ケールは
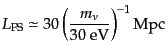 |
|
|
(F.5.115) |
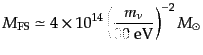 |
|
|
(F.5.116) |
となる。つまり、ニュートリノがダークマターであれば,超銀河団よりも小さ
なスケールのゆらぎは減衰してしまっているということになる.
この場合、構造形成としては超銀河団よりも大きなスケールのゆらぎがはじめ
に成長することになる.このような大構造がまずつくられ,その後その大構造
が小さな銀河などに分裂していくことになる.このような銀河形成のシナリオ
をトップダウン (top-down)型の構造形成という.現在では,このよう
なシナリオによって銀河を作り出すのは難しいことがわかっており,現実的な
ものではないと考えられている.
コールドダークマターは無衝突減衰の効かないようなダークマターである.非
相対論的になる時刻がずっと早くて減衰スケールが無視できるほど小さいよう
なダークマターである.このダークマターのモデルは構造形成にとって都合の
悪いゆらぎの減衰がないため,観測との一致もよく,現在標準的なモデルになっ
ている.ホットダークマターの場合と異なり,より小さな構造が先に形成され,
それがさらに重力により集まって,より大きな構造を作っていく.このような
構造形成はボトムアップ(bottom-up)型と呼ばれる.





次へ: 密度ゆらぎの相関関数とパワースペクトル
上へ: 構造の形成
前へ: バリオン宇宙の困難とダークマターの必要性
目次
索引
All rights reserved © T.Matsubara 2004-2010
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11
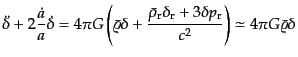
![]() の因
子だけ成長できる.宇宙が晴れ上がった後のバリオンはダークマターのつくる
ポテンシャルの中に落ち込むことによりゆらぎの成長が進む.このプロセスを
調べてみる.まず,ダークマターとバリオンの混合系におけるバリオンゆらぎ
の因
子だけ成長できる.宇宙が晴れ上がった後のバリオンはダークマターのつくる
ポテンシャルの中に落ち込むことによりゆらぎの成長が進む.このプロセスを
調べてみる.まず,ダークマターとバリオンの混合系におけるバリオンゆらぎ
![]() の線形成長は式(6.1.23)から
の線形成長は式(6.1.23)から
![]() とすると,時間間隔
とすると,時間間隔![]() の間に共動距離
の間に共動距離![]() 走るならば,
走るならば,
![]() である.したがって粒子の自由運動のスケールは共動距離にして
である.したがって粒子の自由運動のスケールは共動距離にして
![]() とするとき、無衝突減衰のスケールを求め
てみよう。ダークマターが非相対論的になる温度は
とするとき、無衝突減衰のスケールを求め
てみよう。ダークマターが非相対論的になる温度は
![]() の値は構造形成に多大な影響がある.そこで,
ダークマターは大きく2種類に分けられることになる.一つは無衝突減衰の影
響の大きいホットダークマター (Hot dark matter; HDM)であり,もう
一つは無衝突減衰のほとんど効かないコールドダー
クマター (Cold dark matter; CDM)である.
の値は構造形成に多大な影響がある.そこで,
ダークマターは大きく2種類に分けられることになる.一つは無衝突減衰の影
響の大きいホットダークマター (Hot dark matter; HDM)であり,もう
一つは無衝突減衰のほとんど効かないコールドダー
クマター (Cold dark matter; CDM)である.
![]() となるので、自由運動の共動スケールおよびその質量ス
ケールは
となるので、自由運動の共動スケールおよびその質量ス
ケールは
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11