




次へ: 相対論的摂動論
上へ: 相対論的運動学
前へ: 膨張宇宙における光子と電子の相互作用
目次
索引
Subsections
上では衝突項の評価において光子の偏光を無視してその強度のみに着目した。
だが、光子の偏光は容易に観測可能な量であり,宇宙論的に重要な情報を含む
ことがあるので,この自由度を正確に取り扱うことを考える.トムソン散乱を
考えるので、以下では電磁場を半古典的に取り扱うことにするI6.
角振動数 で伝播する単色平面電磁波を考える.電場はこの電磁波の進
行方向に垂直な平面内(偏光面)にのみ存在する.そこである点において電磁波
の進行方向を
で伝播する単色平面電磁波を考える.電場はこの電磁波の進
行方向に垂直な平面内(偏光面)にのみ存在する.そこである点において電磁波
の進行方向を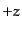 軸にとり,それに垂直な平面内に適当に
軸にとり,それに垂直な平面内に適当に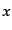 ,
, 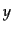 軸をとる.
その点における複素化した電場I7の成分は一般に
軸をとる.
その点における複素化した電場I7の成分は一般に
| |
|
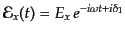 |
(I.4.137) |
| |
|
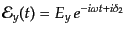 |
(I.4.138) |
で与えられる.ここで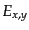 ,
,
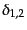 は実の定数であり,それぞ
れ振幅と位相を表している.実部を取ってみればわかるように,この電場は偏
光面において楕円軌道を描く.すなわち単色波は一般に楕円偏光をする.だが,
実際には完全な単色波というものはなく,少しずつ異なる
は実の定数であり,それぞ
れ振幅と位相を表している.実部を取ってみればわかるように,この電場は偏
光面において楕円軌道を描く.すなわち単色波は一般に楕円偏光をする.だが,
実際には完全な単色波というものはなく,少しずつ異なる を持つ平面
波の振幅
を持つ平面
波の振幅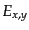 や位相
や位相
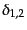 が重ね合わさることにより,光が構
成されている.どんなに狭い
が重ね合わさることにより,光が構
成されている.どんなに狭い の区間をもってきてもその中には無限の
平面波モードが含まれ得るから,ほとんど単色波と見なせる電磁波も,振幅と
位相の異なる平面波を足し合わせたものとなっている.ここで,振幅と位相が
完全にランダムなものであれば足し合わされた電磁波に偏光は発生しないが,
お互いに相関を持っていれば偏光が残ることになる.そこで,
の区間をもってきてもその中には無限の
平面波モードが含まれ得るから,ほとんど単色波と見なせる電磁波も,振幅と
位相の異なる平面波を足し合わせたものとなっている.ここで,振幅と位相が
完全にランダムなものであれば足し合わされた電磁波に偏光は発生しないが,
お互いに相関を持っていれば偏光が残ることになる.そこで, のある
範囲に渡る平均を用いて2次元偏光面上の強度テンソル
のある
範囲に渡る平均を用いて2次元偏光面上の強度テンソル
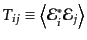 を定義すればこの量が一般の電磁波の偏光の
度合を表すことになる.ただし
を定義すればこの量が一般の電磁波の偏光の
度合を表すことになる.ただし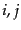 は偏光面上の2次元基底
は偏光面上の2次元基底 のどちらか
をとる.この
のどちらか
をとる.この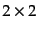 テンソルの成分はエルミート行列となるので,式
(8.3.72)のパウリ行列
テンソルの成分はエルミート行列となるので,式
(8.3.72)のパウリ行列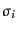 および
および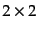 単位行列
単位行列
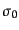 によって一意的に展開できる:
によって一意的に展開できる:
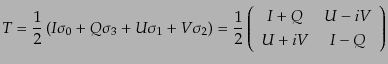 |
(I.4.139) |
ここで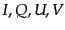 は実の展開係数である.これらの量はストークス・パラメー
タ (Stokes parameters)と呼ばれ,偏光の状態を記述するのに便利な量であ
る.これらはもちろん強度テンソル
は実の展開係数である.これらの量はストークス・パラメー
タ (Stokes parameters)と呼ばれ,偏光の状態を記述するのに便利な量であ
る.これらはもちろん強度テンソル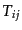 と同等の情報を持っている.
と同等の情報を持っている.
電場の平均値によって具体的にストークス・パラメータを表せば,
| |
|
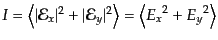 |
(I.4.140) |
| |
|
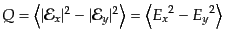 |
(I.4.141) |
| |
|
![$\displaystyle U = \left\langle 2 {\rm Re}\left[ {\cal E}_x^* {\cal E}_y \right] \right\rangle =
\left\langle 2 E_x E_y \cos(\delta_1 - \delta_2) \right\rangle$](img2818.png) |
(I.4.142) |
| |
|
![$\displaystyle V = - \left\langle 2 {\rm Im}\left[ {\cal E}_x^* {\cal E}_y \right] \right\rangle =
\left\langle 2 E_x E_y \sin(\delta_1 - \delta_2) \right\rangle$](img2819.png) |
(I.4.143) |
となる.したがって,変数 は電磁波の強さに比例するパラメータである.
その他のパラメータが非等方な偏光状態を表す.パラメータ
は電磁波の強さに比例するパラメータである.
その他のパラメータが非等方な偏光状態を表す.パラメータ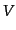 がなければ
がなければ
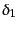 と
と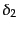 は等しいか
は等しいか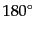 ずれているので直線偏光とな
る.したがって,パラメータ
ずれているので直線偏光とな
る.したがって,パラメータ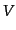 はが偏光の回転性をつくり出している.また,
下に見るようにパラメータ
はが偏光の回転性をつくり出している.また,
下に見るようにパラメータ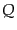 ,
, 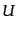 は直線偏光成分を定めている.これらストー
クス・パラメータの間には
は直線偏光成分を定めている.これらストー
クス・パラメータの間には
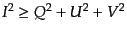 の関係がある.ここで
等号が成り立つのは楕円偏光のときのみである.また,ストークス・パラメー
タが単色平面波の重ね合わせに対する平均量で定義されていることから,加法
性を満たす.すなわち,電磁波を重ね合わせた場合のストークス・パラメータ
は,重ね合わせる前の電磁波のストークス・パラメータを単に足し合わせたも
ので与えられる.
の関係がある.ここで
等号が成り立つのは楕円偏光のときのみである.また,ストークス・パラメー
タが単色平面波の重ね合わせに対する平均量で定義されていることから,加法
性を満たす.すなわち,電磁波を重ね合わせた場合のストークス・パラメータ
は,重ね合わせる前の電磁波のストークス・パラメータを単に足し合わせたも
ので与えられる.
ストークス・パラメータは偏光面の座標 の取り方に依存している.いま,
の取り方に依存している.いま,
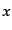 -
-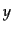 平面の座標軸を光の進行方向から見て時計回りに角度
平面の座標軸を光の進行方向から見て時計回りに角度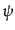 だけ回転
させると,回転行列
だけ回転
させると,回転行列
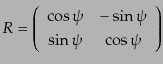 |
(I.4.144) |
により,
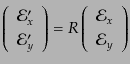 |
(I.4.145) |
となる.このとき式(9.4.139)の変換は
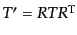 であり,
パウリ行列は
であり,
パウリ行列は
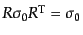 ,
,
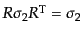 ,
,
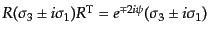 と変換するから
と変換するから と
と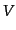 は偏光面の回転
に対して不変であることがわかる.また,
は偏光面の回転
に対して不変であることがわかる.また,
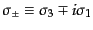 および
および
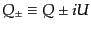 を定義すると都合がよい.この
とき式(9.4.139)は
を定義すると都合がよい.この
とき式(9.4.139)は
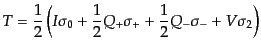 |
(I.4.146) |
と書き直せるから,これらの新たな変数の変換は対角形
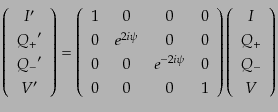 |
(I.4.147) |
であることがわかる.これをもとのストークス・パラメータで表し直せば,
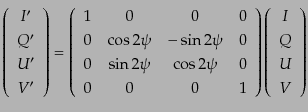 |
(I.4.148) |
となる.こうしてストークス・パラメータ ,
, 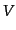 は偏光面の座標に依らない
不変量であるが,
は偏光面の座標に依らない
不変量であるが,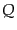 ,
, 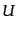 は座標に依存する.これは
は座標に依存する.これは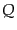 ,
, 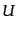 が直線偏光に関
連したパラメータだからである.変換(9.4.148)から
が直線偏光に関
連したパラメータだからである.変換(9.4.148)から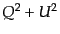 は不変
量である.また角度
は不変
量である.また角度
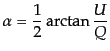 |
(I.4.149) |
は
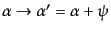 と変換するので,この角度
は座標に依らない固定した方向を決めている.つまり,物理的に観測可能な偏
光ベクトル
と変換するので,この角度
は座標に依らない固定した方向を決めている.つまり,物理的に観測可能な偏
光ベクトル
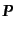 としていま考えている座標系で,
としていま考えている座標系で,
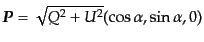 |
(I.4.150) |
を定義することができる.つまり,これは偏光面上にあって大きさが
 で極座標角が
で極座標角が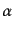 となるベクトルである.直線偏光
となるベクトルである.直線偏光
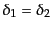 の場合には電場の向きが
の場合には電場の向きが
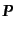 の定義する直線上に
あることが確かめられる.ここで
の定義する直線上に
あることが確かめられる.ここで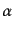 はその定義(9.4.149)によっ
て
はその定義(9.4.149)によっ
て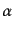 と
と
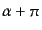 が区別されない.すなわち
が区別されない.すなわち
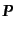 はある方向
を定めるが,その逆向きの方向も区別しないものとする.これは偏光の概念に
沿っている.こうして,ストークス・パラメータの物理的な内容としては,
はある方向
を定めるが,その逆向きの方向も区別しないものとする.これは偏光の概念に
沿っている.こうして,ストークス・パラメータの物理的な内容としては,
 ,
, 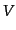 が上述のように光自体の強さと回転偏光成分の強さをそれぞれ表し,
が上述のように光自体の強さと回転偏光成分の強さをそれぞれ表し,
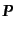 が直線偏光成分の強さと向きを表している.
が直線偏光成分の強さと向きを表している.
最後にストークス・パラメータのパリティを調べておく.偏光面上のパリティ
変換
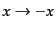 もしくは
もしくは
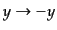 のどちらかを考えれば
のどちらかを考えれば
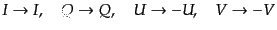 |
(I.4.151) |
と変換することがわかる.つまり, ,
, 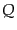 パリティは正,
パリティは正,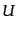 ,
, 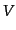 のパリティ
は負である.また,
のパリティ
は負である.また,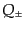 は
は
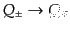 |
(I.4.152) |
と変換し,パリティ変換に関してお互いに入れ替わる.
次にトムソン散乱において偏光の自由度がどのように伝搬するかを考える.い
ま式(9.4.137), (9.4.138)で与えられる平面単色波を考え,図
9.1のように散乱前後の偏光面の座標をとる.
このとき,どちらの座標でも散乱面が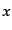 -
-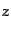 平面内にある.トムソン散乱の
断面積は入射電子の静止系で式(8.7.483)すなわち,
平面内にある.トムソン散乱の
断面積は入射電子の静止系で式(8.7.483)すなわち,
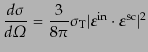 |
(I.4.153) |
で与えられる.入射前後の1に規格化された偏光ベクトル
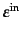 ,
,
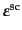 に対して散乱
確率は
に対して散乱
確率は
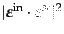 の角度依存性を持っている.したがって散乱前の電場ベクトルを
の角度依存性を持っている.したがって散乱前の電場ベクトルを
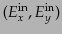 ,位相を
,位相を
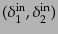 とし,散乱後のものを
とし,散乱後のものを
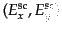 ,
,
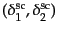 とするとこれらの間には
とするとこれらの間には
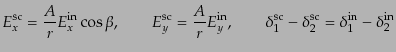 |
(I.4.154) |
の関係がある.ただし,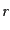 は散乱点からの距離,また
は散乱点からの距離,また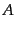 は比例定数でありす
ぐ後に決める.この関係からストークス・パラメータ
(9.4.140)-(9.4.143)の関係を求めれば,散乱前のストークス・
パラメータを
は比例定数でありす
ぐ後に決める.この関係からストークス・パラメータ
(9.4.140)-(9.4.143)の関係を求めれば,散乱前のストークス・
パラメータを
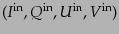 , 散乱後の
ストークス・パラメータを
, 散乱後の
ストークス・パラメータを
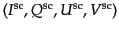 として
として
| |
|
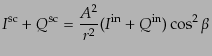 |
(I.4.155) |
| |
|
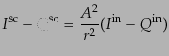 |
(I.4.156) |
| |
|
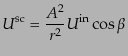 |
(I.4.157) |
| |
|
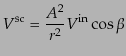 |
(I.4.158) |
となる.ここで,偏光していない入射波
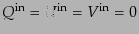 を考えてみるとその全散乱断面積は
を考えてみるとその全散乱断面積は
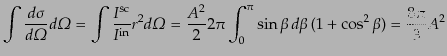 |
(I.4.159) |
となるが,これは
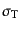 に等しいから
に等しいから
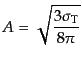 |
(I.4.160) |
であることがわかる.したがって,行列表示を用いて
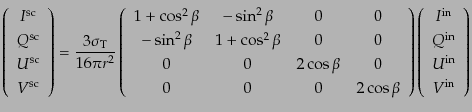 |
(I.4.161) |
となる.あるいは の基底では
の基底では
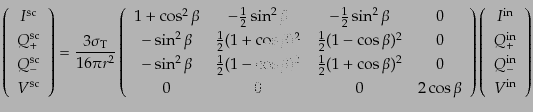 |
(I.4.162) |
となる.この散乱行列は入射方向と散乱方向で図9.1)のように別々
に選んだ座標系で,ストークス・パラメータの基底の方向決めている.だが,
一般に多数の衝突を扱う場合,ある一回の衝突に固有の座標系を選ぶことは適
切ではない.そこでこれを一般の座標系で表現する必要がある.そのためには
全く一般の座標系での入射電磁波のストークス・パラメータを上で考えている
散乱前の座標系へ変換し,それを上の衝突行列で散乱電磁波のものへ変換した
後,散乱後のストークス・パラメータの基底を元の座標のものへと直す必要が
ある.このとき,座標系の変換において偏光面が回転するときのみストークス・
パラメータが変換(9.4.148) を受ける.こうして計算することにより一
般の座標系での散乱行列の式が得られる
I8.
この計算は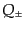 の基底においてよりエレガントに行うことができる
I9 ので,
以下ではその方法を採用する.そのためにはスピン球面調和関数
の基底においてよりエレガントに行うことができる
I9 ので,
以下ではその方法を採用する.そのためにはスピン球面調和関数
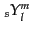 が有用である.スピン球面調和関数はオイラー角
が有用である.スピン球面調和関数はオイラー角
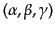 に対するSO(3)回転行列I10
に対するSO(3)回転行列I10
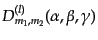 によ
り次のように定義される:
によ
り次のように定義される:
このスピン球面調和関数を用いると一般の回転行列は
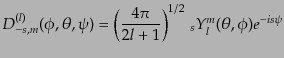 |
(I.4.164) |
と表される.スピンゼロ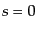 のスピン球面調和関数は通常の球面調和関数に
一致する:
のスピン球面調和関数は通常の球面調和関数に
一致する:
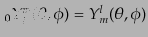 |
(I.4.165) |
また,回転行列の対称性から,
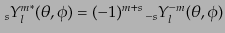 |
(I.4.166) |
となる.さらに回転行列の直交性および完全性により,
| |
|
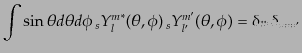 |
(I.4.167) |
| |
|
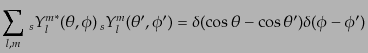 |
(I.4.168) |
が満たされる.また空間反転に対するパリティは
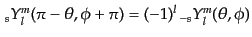 |
(I.4.169) |
である.経度方向の積分に対し,
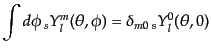 |
(I.4.170) |
が成り立つ.また,回転行列の球面上の点
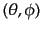 が北極点くるよう
に回転し,そこから点
が北極点くるよう
に回転し,そこから点
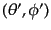 へもっていくという2つの連続した回
転を考える(図9.2).
へもっていくという2つの連続した回
転を考える(図9.2).
図 9.2:
加法定理および一般座標でのトムソン散乱の空間配置の説明図
|
|
その回転は回転演算子を用いて
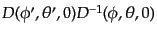 で与えられる(引数はオイラー角).この回転はまた図の角度
で与えられる(引数はオイラー角).この回転はまた図の角度
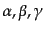 により,一度の回転
により,一度の回転
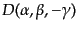 に等し
いから,回転行列について,次の関係が成り立つ:
に等し
いから,回転行列について,次の関係が成り立つ:
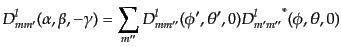 |
(I.4.171) |
したがってスピン球面調和関数について次の加法定理
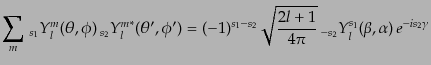 |
(I.4.172) |
が導かれる.
ここまでの準備の下,散乱行列(9.4.162)をスピン球面調和関数で書き
換えることを考える.そうすることにより座標回転に対する変換性があらわに
なるからである.次の具体的な表現
| |
|
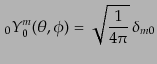 |
(I.4.173) |
| |
|
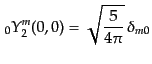 |
(I.4.174) |
| |
|
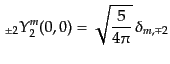 |
(I.4.175) |
および表9.1
表 9.1:
スピン0
および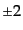 の4重極(
の4重極(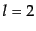 )スピン球面調和関数
)スピン球面調和関数
|
|
の具体形を用いて式(9.4.162)を書き換えると,
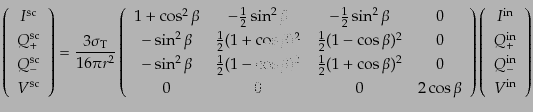 |
(I.4.176) |
となる.ただし,
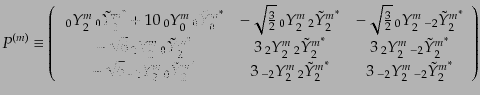 |
(I.4.177) |
また,
 |
(I.4.178) |
という記法を使っている.
ここに現れている の和で表される量は,式(9.4.172)により,一般
の座標系に移ったときにどのような変換をするかが明らかである.式
(9.4.172)の右辺の
の和で表される量は,式(9.4.172)により,一般
の座標系に移ったときにどのような変換をするかが明らかである.式
(9.4.172)の右辺の ,
, 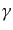 の依存性は
の依存性は
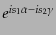 であること,また図9.2により
であること,また図9.2により
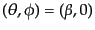 ,
,
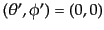 のとき
のとき
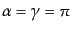 であることから,
であることから,
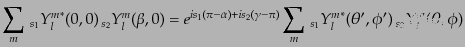 |
(I.4.179) |
という関係がある.また,図9.2において,オイラー角
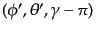 で表される回転を行うと
で表される回転を行うと
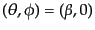 ,
,
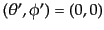 という座標となる.ここで散乱行列
をかけて
という座標となる.ここで散乱行列
をかけて
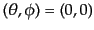 ,
,
 という
座標に移ったあと,オイラー角
という
座標に移ったあと,オイラー角
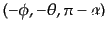 で表される回転
により,元の座標系に戻る.このプロセスで偏光面の座標軸
で表される回転
により,元の座標系に戻る.このプロセスで偏光面の座標軸
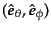 の回転は,光の進行方向から
見て時計回りに,散乱前
の回転は,光の進行方向から
見て時計回りに,散乱前
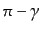 , 散乱後
, 散乱後
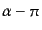 である.したがっ
て散乱前後のストークスパラメータを基底
である.したがっ
て散乱前後のストークスパラメータを基底
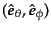 で定義している場合,一般座
標での入射波のストークス・パラメータ
で定義している場合,一般座
標での入射波のストークス・パラメータ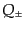 に
に
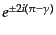 をかけたものを式(9.4.176)の
をかけたものを式(9.4.176)の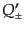 に用いることになる.また,左
辺を一般座標に戻すときには
に用いることになる.また,左
辺を一般座標に戻すときには
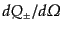 に対して
に対して
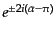 がかかる.これらの位相は式(9.4.176)に式(9.4.179)を
代入したときにすべてキャンセルするから,結局式(9.4.176)の変換行
列のスピン球面調和関数を一般座標のもの
がかかる.これらの位相は式(9.4.176)に式(9.4.179)を
代入したときにすべてキャンセルするから,結局式(9.4.176)の変換行
列のスピン球面調和関数を一般座標のもの
 |
(I.4.180) |
に置き換えればそのまま式(9.4.176)は一般座標でも正しいことがわか
る.
さて,一様な放射場を考え,進行方向が微小立体角
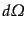 に入る光のストー
クス・パラメータ
に入る光のストー
クス・パラメータ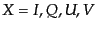 の強さを
の強さを
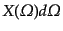 と書くことにす
る.ここで,方向を表すのに
と書くことにす
る.ここで,方向を表すのに
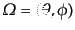 などの記号を用いる.
つまり
などの記号を用いる.
つまり
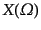 は方向
は方向
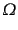 へ進む光の立体角あたりのストークス・
パラメータである.入射波のストークス・パラメータが
へ進む光の立体角あたりのストークス・
パラメータである.入射波のストークス・パラメータが
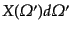 で与えられるとき,微小立体角
で与えられるとき,微小立体角
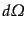 への散乱波
のストークス・パラメータを
への散乱波
のストークス・パラメータを
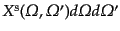 とする.この場合,上の散乱行列の式において
とする.この場合,上の散乱行列の式において
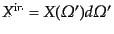 ,
,
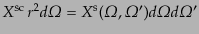 と対応するので,
と対応するので,
| |
|
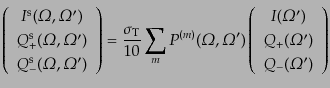 |
(I.4.181) |
| |
|
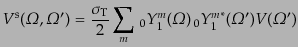 |
(I.4.182) |
となる.ただし,
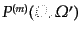 は式(9.4.177)で
は式(9.4.177)で
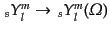 ,
,
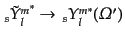 とおいた行列である.
とおいた行列である.
さて,上の式において散乱前の方向
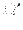 を積分すると,さまざまな方向
からやってくる電磁波がある固定された方向
を積分すると,さまざまな方向
からやってくる電磁波がある固定された方向
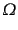 に散乱されるときのス
トークス・パラメータを表すことになる.電子が数密度
に散乱されるときのス
トークス・パラメータを表すことになる.電子が数密度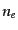 で分布している
とすると,一様な光は単位面積,単位時間あたり
で分布している
とすると,一様な光は単位面積,単位時間あたり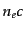 個の電子と散乱を起
こすので,ある方向
個の電子と散乱を起
こすので,ある方向
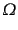 へのストークス・パラメータは単位時間あたり
へのストークス・パラメータは単位時間あたり
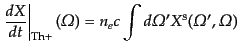 |
(I.4.183) |
だけ散乱により増加することになる.また,もとから
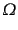 方向を向いて
いた光が散乱された分はそのストークス・パラメータが減少することになる.
その減少分は
方向を向いて
いた光が散乱された分はそのストークス・パラメータが減少することになる.
その減少分は
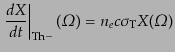 |
(I.4.184) |
である.したがって,ある固定した方向のストークス・パラメータの変化率は
合わせて
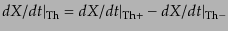 で与え
られる.
で与え
られる.
ここで,ストークス・パラメータをスピン球面調和関数により展開し
| |
|
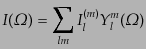 |
(I.4.185) |
| |
|
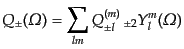 |
(I.4.186) |
| |
|
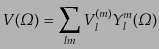 |
(I.4.187) |
とする.展開係数は式(9.4.167)から,
| |
|
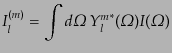 |
(I.4.188) |
| |
|
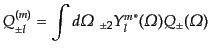 |
(I.4.189) |
| |
|
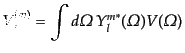 |
(I.4.190) |
で与えられる.すると,ストークス・パラメータの散乱による変化率は
| |
|
![$\displaystyle \left.\frac{dI}{dt}\right\vert _{\rm Th} =
n_e c \sigma_{\rm T}
...
...\left(Q_{+2}^{(m)} + Q_{-2}^{(m)}\right)
\right]Y_2^m({\mit\Omega})
\right\}$](img2948.png) |
|
| |
|
|
(I.4.191) |
| |
|
![$\displaystyle \left.\frac{dQ_\pm}{dt}\right\vert _{\rm Th} =
n_e c \sigma_{\rm...
... + Q_{-2}^{(m)}\right)
\right]{{ }_{\pm 2}Y_{2}^{m}}({\mit\Omega})
\right\}$](img2949.png) |
|
| |
|
|
(I.4.192) |
| |
|
![$\displaystyle \left.\frac{dV}{dt}\right\vert _{\rm Th} =
n_e c \sigma_{\rm T} ...
...V({\mit\Omega}) +
\frac12 \sum_{m=-1}^1 V_1^{(m)} Y_1^m({\mit\Omega})
\right]$](img2950.png) |
(I.4.193) |
となる.この式により多数の光子系の偏極分布の時間変化が記述できる.ストー
クス・パラメータを光子のエネルギーの関数と考え,さらに時空点の場所にも
依存する場の量と考えると,偏極状態の分布関数とみなすことができる.する
とこれらの式はボルツマン方程式における単位時間あたりの衝突項となる.し
たがって,ストークス・パラメータ
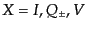 に対して上の衝突項によ
るボルツマン方程式は
に対して上の衝突項によ
るボルツマン方程式は
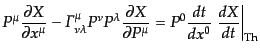 |
(I.4.194) |
となる.
Footnotes
- ...
考えるので、以下では電磁場を半古典的に取り扱うことにするI6
- 結果
は同じだが,完全に量子論的な取り扱いは A. Kosowsky, Ann. Phys. 246, 49 (1996)を見よ.
- ...
その点における複素化した電場I7
- 電磁波における複素化した電場とは,
その実部が実際の電場を与えるようなものである.
- ...
般の座標系での散乱行列の式が得られるI8
- S. Chandrasekhar, Radiative Transfer, Dover
Publications (New York, 1960)
- ... の基底においてよりエレガントに行うことができるI9
- U. Seljak & M. Zaldarriaga, Phys. Rev. Lett. 78, 2054
(1997); S. Hu, & M. White, Phys. Rev. D, 56, 596 (1997)
- ...に対するSO(3)回転行列I10
- 回転行列の定義,性質につ
いては例えば,M.E.ローズ,角運動量の基礎理論(山内恭彦,森田正人訳,み
すず書房,1971)を見よ.





次へ: 相対論的摂動論
上へ: 相対論的運動学
前へ: 膨張宇宙における光子と電子の相互作用
目次
索引
All rights reserved © T.Matsubara 2004-2010
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11
![]() で伝播する単色平面電磁波を考える.電場はこの電磁波の進
行方向に垂直な平面内(偏光面)にのみ存在する.そこである点において電磁波
の進行方向を
で伝播する単色平面電磁波を考える.電場はこの電磁波の進
行方向に垂直な平面内(偏光面)にのみ存在する.そこである点において電磁波
の進行方向を![]() 軸にとり,それに垂直な平面内に適当に
軸にとり,それに垂直な平面内に適当に![]() ,
, ![]() 軸をとる.
その点における複素化した電場I7の成分は一般に
軸をとる.
その点における複素化した電場I7の成分は一般に
![]() の取り方に依存している.いま,
の取り方に依存している.いま,
![]() -
-![]() 平面の座標軸を光の進行方向から見て時計回りに角度
平面の座標軸を光の進行方向から見て時計回りに角度![]() だけ回転
させると,回転行列
だけ回転
させると,回転行列
![]() もしくは
もしくは
![]() のどちらかを考えれば
のどちらかを考えれば
![]() の基底においてよりエレガントに行うことができる
I9 ので,
以下ではその方法を採用する.そのためにはスピン球面調和関数
の基底においてよりエレガントに行うことができる
I9 ので,
以下ではその方法を採用する.そのためにはスピン球面調和関数
![]() が有用である.スピン球面調和関数はオイラー角
が有用である.スピン球面調和関数はオイラー角
![]() に対するSO(3)回転行列I10
に対するSO(3)回転行列I10
![]() によ
り次のように定義される:
によ
り次のように定義される:
![]() の和で表される量は,式(9.4.172)により,一般
の座標系に移ったときにどのような変換をするかが明らかである.式
(9.4.172)の右辺の
の和で表される量は,式(9.4.172)により,一般
の座標系に移ったときにどのような変換をするかが明らかである.式
(9.4.172)の右辺の![]() ,
, ![]() の依存性は
の依存性は
![]() であること,また図9.2により
であること,また図9.2により
![]() ,
,
![]() のとき
のとき
![]() であることから,
であることから,
![]() に入る光のストー
クス・パラメータ
に入る光のストー
クス・パラメータ![]() の強さを
の強さを
![]() と書くことにす
る.ここで,方向を表すのに
と書くことにす
る.ここで,方向を表すのに
![]() などの記号を用いる.
つまり
などの記号を用いる.
つまり
![]() は方向
は方向
![]() へ進む光の立体角あたりのストークス・
パラメータである.入射波のストークス・パラメータが
へ進む光の立体角あたりのストークス・
パラメータである.入射波のストークス・パラメータが
![]() で与えられるとき,微小立体角
で与えられるとき,微小立体角
![]() への散乱波
のストークス・パラメータを
への散乱波
のストークス・パラメータを
![]() とする.この場合,上の散乱行列の式において
とする.この場合,上の散乱行列の式において
![]() ,
,
![]() と対応するので,
と対応するので,
![]() を積分すると,さまざまな方向
からやってくる電磁波がある固定された方向
を積分すると,さまざまな方向
からやってくる電磁波がある固定された方向
![]() に散乱されるときのス
トークス・パラメータを表すことになる.電子が数密度
に散乱されるときのス
トークス・パラメータを表すことになる.電子が数密度![]() で分布している
とすると,一様な光は単位面積,単位時間あたり
で分布している
とすると,一様な光は単位面積,単位時間あたり![]() 個の電子と散乱を起
こすので,ある方向
個の電子と散乱を起
こすので,ある方向
![]() へのストークス・パラメータは単位時間あたり
へのストークス・パラメータは単位時間あたり
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11