




次へ: 高次相関関数
上へ: 天体分布の統計理論
前へ: 天体分布の統計理論
目次
索引
Subsections
天体分布の相関関数とパワースペクトル
天体分布の相関関数
観測量である銀河などの天体の空間分布は理論的に求められる密度ゆらぎと関
係しているが,前者が空間的な点の分布であるのに対して,後者は連続的な場
の分布である.そこで,相関関数などの統計量について,これらの間の関係を
知る必要がある.そこで,まず天体分布の相関関数を観測に対応させて定義す
る.
ここでは,銀河分布の相関関数を例にとって説明する.まずある銀河に着目し,
その銀河から距離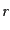 だけ離れた微小体積
だけ離れた微小体積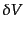 の中に他の銀河を見つけ
る確率
の中に他の銀河を見つけ
る確率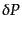 を考える.これはもし分布が完全にランダムなポアソン分布
をしているならば,銀河の平均数密度を
を考える.これはもし分布が完全にランダムなポアソン分布
をしているならば,銀河の平均数密度を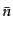 として,
として,
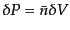 |
(O.1.1) |
で与えられる.実際にはクラスタリングがあるため,ある銀河のそばには平均
的に他の銀河がより多く存在したりする.そのため,この確率は式
(15.1.1)からずれることになる.そここでこのずれを考慮したときの
確率を
![$\displaystyle \delta P = \bar{n} \delta V \left[1 + \xi_{\rm g}(r)\right]$](img4353.png) |
(O.1.2) |
とおくことができる.ここで,
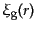 はランダムな分布からのず
れを表すもので,これが銀河の相関関数(correlation function)である.
密度分布の相関関数と区別するため,銀河と銀河の相関という意味を表す添字
ggをつけてある.いま,分布の統計的性質は宇宙の場所や方向によらないと仮
定すると,この相関関数は物理的距離
はランダムな分布からのず
れを表すもので,これが銀河の相関関数(correlation function)である.
密度分布の相関関数と区別するため,銀河と銀河の相関という意味を表す添字
ggをつけてある.いま,分布の統計的性質は宇宙の場所や方向によらないと仮
定すると,この相関関数は物理的距離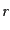 のみの関数になるO1.これはスケール
のみの関数になるO1.これはスケール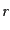 のクラスタリングの程度
を表していることがわかるであろう.ある距離
のクラスタリングの程度
を表していることがわかるであろう.ある距離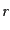 における相関関数が正であ
れば,ある銀河のまわりの距離
における相関関数が正であ
れば,ある銀河のまわりの距離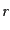 のスケールでは平均的にランダムな場合に
期待されるよりも多い数の銀河が存在する.これは正の相関を持つ場合である.
逆に相関関数が負であれば,より少ない銀河しか存在しない.これは負の相関
を持つ場合である.
のスケールでは平均的にランダムな場合に
期待されるよりも多い数の銀河が存在する.これは正の相関を持つ場合である.
逆に相関関数が負であれば,より少ない銀河しか存在しない.これは負の相関
を持つ場合である.
銀河の相関関数はまた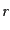 だけ離れた2点においた微小体積
だけ離れた2点においた微小体積
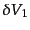 ,
,
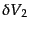 の中に銀河が同時に入る確率
の中に銀河が同時に入る確率
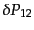 からも求められる.
上で考えた確率
からも求められる.
上で考えた確率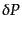 は
は
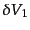 に銀河があるときに
に銀河があるときに
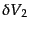 に
銀河が入る条件付き確率
に
銀河が入る条件付き確率
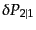 であり,これは
であり,これは
![$\displaystyle \delta P_{2\vert 1} = \bar{n} \delta V_2 \left[1 + \xi_{\rm g}(r)\right]$](img4358.png) |
(O.1.3) |
である.ここで,条件なしで
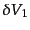 に銀河が入る確率は
に銀河が入る確率は
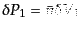 であるから,確率の伝播規則より,
であるから,確率の伝播規則より,
![$\displaystyle \delta P_{12} = \delta P_1\cdot \delta P_{2\vert 1} = \bar{n}^2 \delta V_1 \delta V_2 \left[1 + \xi_{\rm g}(r)\right]$](img4360.png) |
(O.1.4) |
となる.
銀河の3次元的空間分布を調べる銀河サーベイによって,我々の宇宙の銀河な
どの相関関数が得られている.その結果,相関関数はよい近似で巾的なふるま
いをすることがわかっている.銀河,銀河団,および超銀河団についての相関
関数をそれぞれ
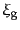 ,
,
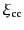 ,
,
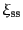 とすると,
観測的に次のようになることが知られている:
とすると,
観測的に次のようになることが知られている:
これをみると,銀河団や超銀河団も銀河と同じ巾の値を持っていることが特徴
的である.また,相関関数がちょうど1になる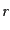 の値を相関距離という.相関
距離は銀河,銀河団,超銀河団,となるにつれて増えていることがわかる.大
きな距離では相関関数は必ず負となる場所があるので,巾的なふるまいはずっ
と続くわけではないが,かなり大きなスケールまで単純なふるまいをしている
ことがわかる.
の値を相関距離という.相関
距離は銀河,銀河団,超銀河団,となるにつれて増えていることがわかる.大
きな距離では相関関数は必ず負となる場所があるので,巾的なふるまいはずっ
と続くわけではないが,かなり大きなスケールまで単純なふるまいをしている
ことがわかる.
これら相関関数のふるまいは構造形成の理論が定量的に説明すべき観測結果で
ある.宇宙モデルによって,理論的に導かれるこれらの相関関数のふるまいは
大幅に異なるので,これらの相関関数を定量的に再現できる理論があるかどう
かを探すことは,観測的宇宙論の主要な手法の一つである.
連続的な密度ゆらぎとの関係
上のように観測的に得られる相関関数は理論的に計算される連続的な関数の密
度ゆらぎと結び付ける必要がある.この関係をみるため,空間を微小体積
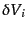 に分割して,その中心の座標を
に分割して,その中心の座標を
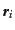 とし,この微小体積
の中にある銀河の数を
とし,この微小体積
の中にある銀河の数を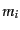 とする.体積の小さい極限をとると,中に入る銀
河の数は0か1のみになるので,
とする.体積の小さい極限をとると,中に入る銀
河の数は0か1のみになるので,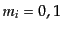 のみである.分布が統計的に一様
な場合,空間的に平均した数密度は一定で,
のみである.分布が統計的に一様
な場合,空間的に平均した数密度は一定で,
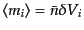 である.ここで,
である.ここで,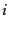 番目と
番目と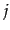 番目の微小体積に同時に銀
河が入る確率
番目の微小体積に同時に銀
河が入る確率
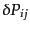 を考える.これは,式(15.1.4)により,
相関関数を用いて
を考える.これは,式(15.1.4)により,
相関関数を用いて
![$\displaystyle \delta P_{ij} = \bar{n}^2 \delta V_i \delta V_j \left[1 + \xi_{\rm g}(r_{ij})\right]$](img4375.png) |
(O.1.8) |
と表される.ここで,
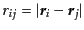 とした.この確率
は,積
とした.この確率
は,積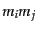 が,両方に銀河が入るときのみ1でその他の場合は0 になるこ
とから,
が,両方に銀河が入るときのみ1でその他の場合は0 になるこ
とから,
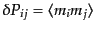 |
(O.1.9) |
とも表される.ここで,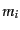 ,
, 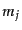 は連続的な場である密度ゆらぎの値を離
散的に表現しているものとしよう.すなわち,場所
は連続的な場である密度ゆらぎの値を離
散的に表現しているものとしよう.すなわち,場所
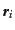 における微小
体積
における微小
体積
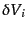 の中に銀河が入る確率を
の中に銀河が入る確率を
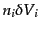 とするとき,
とするとき,
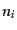 はその点での密度ゆらぎ
はその点での密度ゆらぎ
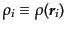 に比例すると
仮定する.これをポアソンモデル(Poisson model)という.背景にある
密度場を銀河などの天体がポアソン分布によって表現していると考えるわけで
ある.これはモデルであって,実際には密度場と銀河の数密度にはもっと複雑
な関係がある可能性もある.このような後者の場合,銀河分布がバイア
スされている(biased)といわれる.ここでは簡単のため,バイアスされてい
ない,単純なポアソンモデルを仮定することにする.この場合,質量密度と銀
河の数密度の比例係数を
に比例すると
仮定する.これをポアソンモデル(Poisson model)という.背景にある
密度場を銀河などの天体がポアソン分布によって表現していると考えるわけで
ある.これはモデルであって,実際には密度場と銀河の数密度にはもっと複雑
な関係がある可能性もある.このような後者の場合,銀河分布がバイア
スされている(biased)といわれる.ここでは簡単のため,バイアスされてい
ない,単純なポアソンモデルを仮定することにする.この場合,質量密度と銀
河の数密度の比例係数を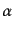 とおくと,
とおくと,
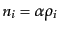 , また,
, また,
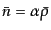 となる.
となる.
ここで式(15.1.8)の平均は空間平均であるが,これを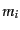 ,
, 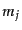 が
統計的に揺らいでいると考えて,エルゴード仮説により,変数に対するアンサ
ンブル平均でおきかえてもよいと考える.エルゴード仮説では統計平均は体積
が無限に大きい極限での空間平均と同定されるが,実際の観測では無限に広い
空間を平均することはできない.そこで,さらに体積が十分大きければやはり
統計平均で置き換えてもよいという,より狭い仮定をしよう.これはフェ
アサンプル仮説(Fair sample hypothesis)と呼ばれる.すると,
が
統計的に揺らいでいると考えて,エルゴード仮説により,変数に対するアンサ
ンブル平均でおきかえてもよいと考える.エルゴード仮説では統計平均は体積
が無限に大きい極限での空間平均と同定されるが,実際の観測では無限に広い
空間を平均することはできない.そこで,さらに体積が十分大きければやはり
統計平均で置き換えてもよいという,より狭い仮定をしよう.これはフェ
アサンプル仮説(Fair sample hypothesis)と呼ばれる.すると,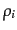 が
与えられたときの
が
与えられたときの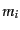 の統計平均は,
の統計平均は,
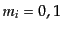 より,
より,
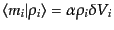 となる.このとき,式
(15.1.8) の平均はこのような
となる.このとき,式
(15.1.8) の平均はこのような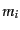 ,
, 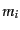 の条件付き平均をさらに密
度の分布で統計平均を取ったものとなる.すると,
の条件付き平均をさらに密
度の分布で統計平均を取ったものとなる.すると,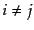 のときは,
のときは,
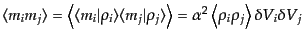 |
(O.1.10) |
となる.また,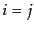 のときは
のときは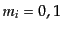 より,
より,
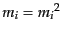 であるため,
であるため,
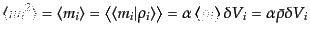 |
(O.1.11) |
となる.したがって式(15.1.8)はクロネッカーデルタ
 |
(O.1.12) |
を用いて,
![$\displaystyle \delta P_{ij} = \bar{n}^2 \delta V_i \delta V_j \left[ \frac{\lan...
... - \frac{\langle\rho_i \rho_j \rangle}{\bar{\rho}^2} \right)\delta_{ij} \right]$](img4392.png) |
(O.1.13) |
となる.ここで,
 の極限をとるとき,
の極限をとるとき,
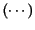 の中の第2項は第1項に比べて無視でき,またクロネッカーデルタは
の中の第2項は第1項に比べて無視でき,またクロネッカーデルタは
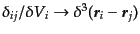 の
ようにディラックのデルタ関数になる. こうして,式(15.1.8)より
の
ようにディラックのデルタ関数になる. こうして,式(15.1.8)より
となることがわかる.ここで,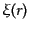 は連続的な密度ゆらぎの相関関数であ
る.密度ゆらぎの相関関数は連続的な場の分布から求められるのに対し,銀河
の相関関数は離散的な点分布から求められるために,原点で特異なデルタ関数
がよけいにつけ加わることになる.このよけいな項はショットノイズ項
(shot-noise term)と呼ばれる.こうして,観測量である相関関数が純粋に理
論的に予言される量で書き表されたことになる.
は連続的な密度ゆらぎの相関関数であ
る.密度ゆらぎの相関関数は連続的な場の分布から求められるのに対し,銀河
の相関関数は離散的な点分布から求められるために,原点で特異なデルタ関数
がよけいにつけ加わることになる.このよけいな項はショットノイズ項
(shot-noise term)と呼ばれる.こうして,観測量である相関関数が純粋に理
論的に予言される量で書き表されたことになる.
天体分布のパワースペクトル
パワースペクトルについても同様に,離散的な点分布からどのように求められ
るかを考えてみる.まず,銀河が
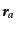 ,
,
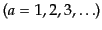 という
場所にあるとする.このような離散的な分布のフーリエ変換は
という
場所にあるとする.このような離散的な分布のフーリエ変換は
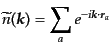 |
(O.1.15) |
であり,これが観測量に対応する.ここで,この観測量によってゆらぎに対応
する量を定義するため,上式の平均値が何か調べてみる.
そのために,観測されている空間全体の体積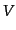 を微小体積に分けること
により,式(15.1.15)は
を微小体積に分けること
により,式(15.1.15)は
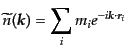 |
(O.1.16) |
と表せる.ここで,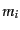 は
は
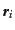 にある微小体積
にある微小体積
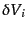 の中に入
る銀河の数である.微小体積は十分小さく,
の中に入
る銀河の数である.微小体積は十分小さく,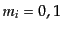 のみをとる.ここで
は簡単のために,銀河は一様にサンプリングされているものと仮定し,銀河の
平均数密度
のみをとる.ここで
は簡単のために,銀河は一様にサンプリングされているものと仮定し,銀河の
平均数密度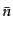 は空間的に一定とする.このとき,観測される体積の中で
は1,外では0をとるウィンドウ関数
は空間的に一定とする.このとき,観測される体積の中で
は1,外では0をとるウィンドウ関数 を定義する:
を定義する:
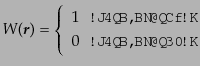 |
(O.1.17) |
すると,式(15.1.16)の平均値は
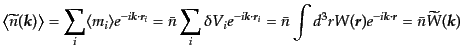 |
(O.1.18) |
である.ここで,
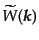 はウィンドウ関数のフーリエ変換
である.したがって,ゆらぎに対応する観測量は,
はウィンドウ関数のフーリエ変換
である.したがって,ゆらぎに対応する観測量は,
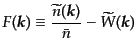 |
(O.1.19) |
である.これも観測量であり,ここから,銀河分布のパワースペクトルを次の
ように定義する:
 |
(O.1.20) |
こうして定義された離散的な分布についてのパワースペクトルが連続的な密度
分布のパワースペクトルとどのように結び付いているかを調べる.そのために
まず,式(15.1.16)の絶対値の2乗の期待値を評価してみると,
となる.これと式(15.1.18)により,上で定義した離散的なパワースペ
クトルの期待値は
となる.これが離散的な分布と連続的な分布のパワースペクトルを結ぶ基本的
な式である.左辺は仮想的な宇宙について平均されたアンサンブル平均なので,
実際には観測量そのものではない.実際の観測ではこれからのずれが生じるこ
とになる.このようなずれをコズミックバリアンス(Cosmic variance)
という.このような不定性を最小限に押えるために,実際の観測では,
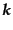 の方向について平均をとり,さらに
の方向について平均をとり,さらに
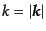 をいくつかの領
域に分けて平均するということが行われる.これによりアンサンブル平均を行
うのに似た効果が加えることができる.
をいくつかの領
域に分けて平均するということが行われる.これによりアンサンブル平均を行
うのに似た効果が加えることができる.
フェアサンプル仮説により,見ようとするゆらぎのスケールに比べて観測体積
が無限に広い極限
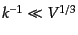 では,観測的に決められる量
では,観測的に決められる量
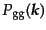 はアンサンブル平均をした式(15.1.22)に近付いて行く.
ここで,観測体積が無限大の極限
はアンサンブル平均をした式(15.1.22)に近付いて行く.
ここで,観測体積が無限大の極限
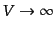 をとると,
をとると,
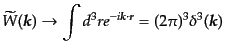 |
(O.1.23) |
となり,さらに,
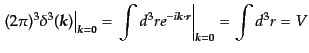 |
(O.1.24) |
に注意すると,
![$\displaystyle \left\vert\widetilde{W}({\mbox{\boldmath$k$}})\right\vert^2 \righ...
...^3({\mbox{\boldmath$k$}})\right]^2 = V (2\pi)^3 \delta^3({\mbox{\boldmath$k$}})$](img4421.png) |
(O.1.25) |
となる.体積無限大の極限
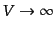 では,式(15.1.20)で
定義した離散的な分布のパワースペクトルは観測体積が実質的にアンサンブル
平均をしたものに帰着することも考慮して,
では,式(15.1.20)で
定義した離散的な分布のパワースペクトルは観測体積が実質的にアンサンブル
平均をしたものに帰着することも考慮して,
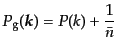 |
(O.1.26) |
となることがわかる.第2項は分布の離散性から来ていて,ショットノイズ項
である.この式はちょうど,式(15.1.14)のフーリエ変換になっている
ことがわかる.
観測体積が十分大きくなければ,ウィンドウ関数のフーリエ変換はもはやデル
タ関数ではなく,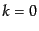 のまわりに有限の幅をもってぼやけた関数となる.こ
こで,観測される離散的なパワースペクトルは式(15.1.22)のように
理論的な密度ゆらぎをウィンドウ関数によってフーリエ空間で畳み込んだもの
となっている.いいかえれば,観測されるパワースペクトルは理論的なパワー
スペクトルを3次元的にある固定した幅でならしたものになっている.ここで,
大スケールのゆらぎに対応する
のまわりに有限の幅をもってぼやけた関数となる.こ
こで,観測される離散的なパワースペクトルは式(15.1.22)のように
理論的な密度ゆらぎをウィンドウ関数によってフーリエ空間で畳み込んだもの
となっている.いいかえれば,観測されるパワースペクトルは理論的なパワー
スペクトルを3次元的にある固定した幅でならしたものになっている.ここで,
大スケールのゆらぎに対応する の絶対値の小さなモードは,波数空間にお
ける体積が小さいため,完全にならされてしまう.このため,大スケールのゆ
らぎは正確に求まらないことになる.これは,もともと,観測体積よりも大き
なスケールのゆらぎを求めることができないことに対応している.
の絶対値の小さなモードは,波数空間にお
ける体積が小さいため,完全にならされてしまう.このため,大スケールのゆ
らぎは正確に求まらないことになる.これは,もともと,観測体積よりも大き
なスケールのゆらぎを求めることができないことに対応している.
Footnotes
- ...のみの関数になるO1
- 一般に
分布が統計的に非一様であったり,非等方であったりすると,相関関数は方向
や絶対的な場所の関数となる.





次へ: 高次相関関数
上へ: 天体分布の統計理論
前へ: 天体分布の統計理論
目次
索引
All rights reserved © T.Matsubara 2004-2010
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11
![]() だけ離れた微小体積
だけ離れた微小体積![]() の中に他の銀河を見つけ
る確率
の中に他の銀河を見つけ
る確率![]() を考える.これはもし分布が完全にランダムなポアソン分布
をしているならば,銀河の平均数密度を
を考える.これはもし分布が完全にランダムなポアソン分布
をしているならば,銀河の平均数密度を![]() として,
として,
![]() だけ離れた2点においた微小体積
だけ離れた2点においた微小体積
![]() ,
,
![]() の中に銀河が同時に入る確率
の中に銀河が同時に入る確率
![]() からも求められる.
上で考えた確率
からも求められる.
上で考えた確率![]() は
は
![]() に銀河があるときに
に銀河があるときに
![]() に
銀河が入る条件付き確率
に
銀河が入る条件付き確率
![]() であり,これは
であり,これは
![]() ,
,
![]() ,
,
![]() とすると,
観測的に次のようになることが知られている:
とすると,
観測的に次のようになることが知られている:
![]() に分割して,その中心の座標を
に分割して,その中心の座標を
![]() とし,この微小体積
の中にある銀河の数を
とし,この微小体積
の中にある銀河の数を![]() とする.体積の小さい極限をとると,中に入る銀
河の数は0か1のみになるので,
とする.体積の小さい極限をとると,中に入る銀
河の数は0か1のみになるので,![]() のみである.分布が統計的に一様
な場合,空間的に平均した数密度は一定で,
のみである.分布が統計的に一様
な場合,空間的に平均した数密度は一定で,
![]() である.ここで,
である.ここで,![]() 番目と
番目と![]() 番目の微小体積に同時に銀
河が入る確率
番目の微小体積に同時に銀
河が入る確率
![]() を考える.これは,式(15.1.4)により,
相関関数を用いて
を考える.これは,式(15.1.4)により,
相関関数を用いて
![]() ,
, ![]() が
統計的に揺らいでいると考えて,エルゴード仮説により,変数に対するアンサ
ンブル平均でおきかえてもよいと考える.エルゴード仮説では統計平均は体積
が無限に大きい極限での空間平均と同定されるが,実際の観測では無限に広い
空間を平均することはできない.そこで,さらに体積が十分大きければやはり
統計平均で置き換えてもよいという,より狭い仮定をしよう.これはフェ
アサンプル仮説(Fair sample hypothesis)と呼ばれる.すると,
が
統計的に揺らいでいると考えて,エルゴード仮説により,変数に対するアンサ
ンブル平均でおきかえてもよいと考える.エルゴード仮説では統計平均は体積
が無限に大きい極限での空間平均と同定されるが,実際の観測では無限に広い
空間を平均することはできない.そこで,さらに体積が十分大きければやはり
統計平均で置き換えてもよいという,より狭い仮定をしよう.これはフェ
アサンプル仮説(Fair sample hypothesis)と呼ばれる.すると,![]() が
与えられたときの
が
与えられたときの![]() の統計平均は,
の統計平均は,
![]() より,
より,
![]() となる.このとき,式
(15.1.8) の平均はこのような
となる.このとき,式
(15.1.8) の平均はこのような![]() ,
, ![]() の条件付き平均をさらに密
度の分布で統計平均を取ったものとなる.すると,
の条件付き平均をさらに密
度の分布で統計平均を取ったものとなる.すると,![]() のときは,
のときは,
![]() ,
,
![]() という
場所にあるとする.このような離散的な分布のフーリエ変換は
という
場所にあるとする.このような離散的な分布のフーリエ変換は
![]() を微小体積に分けること
により,式(15.1.15)は
を微小体積に分けること
により,式(15.1.15)は
![]() では,観測的に決められる量
では,観測的に決められる量
![]() はアンサンブル平均をした式(15.1.22)に近付いて行く.
ここで,観測体積が無限大の極限
はアンサンブル平均をした式(15.1.22)に近付いて行く.
ここで,観測体積が無限大の極限
![]() をとると,
をとると,
![]() のまわりに有限の幅をもってぼやけた関数となる.こ
こで,観測される離散的なパワースペクトルは式(15.1.22)のように
理論的な密度ゆらぎをウィンドウ関数によってフーリエ空間で畳み込んだもの
となっている.いいかえれば,観測されるパワースペクトルは理論的なパワー
スペクトルを3次元的にある固定した幅でならしたものになっている.ここで,
大スケールのゆらぎに対応する
のまわりに有限の幅をもってぼやけた関数となる.こ
こで,観測される離散的なパワースペクトルは式(15.1.22)のように
理論的な密度ゆらぎをウィンドウ関数によってフーリエ空間で畳み込んだもの
となっている.いいかえれば,観測されるパワースペクトルは理論的なパワー
スペクトルを3次元的にある固定した幅でならしたものになっている.ここで,
大スケールのゆらぎに対応する![]() の絶対値の小さなモードは,波数空間にお
ける体積が小さいため,完全にならされてしまう.このため,大スケールのゆ
らぎは正確に求まらないことになる.これは,もともと,観測体積よりも大き
なスケールのゆらぎを求めることができないことに対応している.
の絶対値の小さなモードは,波数空間にお
ける体積が小さいため,完全にならされてしまう.このため,大スケールのゆ
らぎは正確に求まらないことになる.これは,もともと,観測体積よりも大き
なスケールのゆらぎを求めることができないことに対応している.
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11