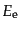 , 観測者に届いたときのエネル
ギーを
, 観測者に届いたときのエネル
ギーを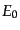 とする.粒子が放出されたときのアフィンパラメータの値
を
とする.粒子が放出されたときのアフィンパラメータの値
を
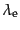 , 粒子が観測されたときの値を
, 粒子が観測されたときの値を
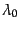 としよ
う.物質の4元速度を
としよ
う.物質の4元速度を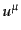 とすると,
とすると,
観測する質量なし粒子のエネルギーは天体などから放出されてから観測者に届
くまでに変化する.一様等方宇宙では,宇宙膨張による赤方偏移によって放出
されたときよりも小さくなる.さらに,宇宙の非一様性を考慮すると,ポテン
シャルの空間的,時間的変化によってもエネルギー変化を受ける.質量なし粒
子が放出された時のエネルギーを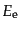 , 観測者に届いたときのエネル
ギーを
, 観測者に届いたときのエネル
ギーを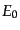 とする.粒子が放出されたときのアフィンパラメータの値
を
とする.粒子が放出されたときのアフィンパラメータの値
を
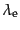 , 粒子が観測されたときの値を
, 粒子が観測されたときの値を
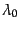 としよ
う.物質の4元速度を
としよ
う.物質の4元速度を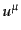 とすると,
とすると,
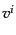 とすると,線形摂動項を含む4元速度
は式(10.4.113)で与えられ,
とすると,線形摂動項を含む4元速度
は式(10.4.113)で与えられ,
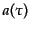 の引数であるコンフォーマル時間は摂動時空
において評価されているので,ゲージ依存している.このため例えば
の引数であるコンフォーマル時間は摂動時空
において評価されているので,ゲージ依存している.このため例えば
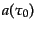 を規格化によって
を規格化によって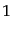 に置き換えてはならない.もし置き換えてし
まうとゲージ依存した規格化をすることになってしまい,その後の結果もゲー
ジ不変ではなくなってしまうからである.量
に置き換えてはならない.もし置き換えてし
まうとゲージ依存した規格化をすることになってしまい,その後の結果もゲー
ジ不変ではなくなってしまうからである.量
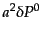 は式
(13.1.16)を積分することにより得ることができ,
は式
(13.1.16)を積分することにより得ることができ,
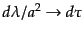 と置き換えてよい.こうして結局
と置き換えてよい.こうして結局
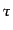 ととも
に変化して,表面積分とはならないことに注意.非摂動項は,粒子が放出され
た時のスケール因子に比例してエネルギーが減る効果を表す.これは以前導い
た,宇宙膨張による赤方偏移の効果である.次の項は視線方向の速度によるドッ
プラー効果によるエネルギーのずれである.ベクトル
ととも
に変化して,表面積分とはならないことに注意.非摂動項は,粒子が放出され
た時のスケール因子に比例してエネルギーが減る効果を表す.これは以前導い
た,宇宙膨張による赤方偏移の効果である.次の項は視線方向の速度によるドッ
プラー効果によるエネルギーのずれである.ベクトル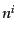 は観測者の視線方向
を向いていて,観測者や粒子の放出源が共動座標に対してお互いに遠ざかるか
近づくかに応じてエネルギーの減少あるいは増加がおこる.次の項は,放出源
と観測者の場所での,ニュートンポテンシャルに対応する摂動
は観測者の視線方向
を向いていて,観測者や粒子の放出源が共動座標に対してお互いに遠ざかるか
近づくかに応じてエネルギーの減少あるいは増加がおこる.次の項は,放出源
と観測者の場所での,ニュートンポテンシャルに対応する摂動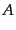 の値の差によっ
て生じるエネルギー変化であり,重力的赤方偏移に対応する.この部分の寄与
は通常ザックス・ヴォルフェ効果(Sachs-Wolfe effect)と呼ばれるものである.また,最後の粒子の軌跡に沿った積分は,計
量の時間変化が粒子のエネルギーに変化を及ぼすことを示しており,これ
は積分されたザックス・ヴォルフェ効果 (Integrated Sachs-Wolfe
effect)と呼ばれる
ものである.
の値の差によっ
て生じるエネルギー変化であり,重力的赤方偏移に対応する.この部分の寄与
は通常ザックス・ヴォルフェ効果(Sachs-Wolfe effect)と呼ばれるものである.また,最後の粒子の軌跡に沿った積分は,計
量の時間変化が粒子のエネルギーに変化を及ぼすことを示しており,これ
は積分されたザックス・ヴォルフェ効果 (Integrated Sachs-Wolfe
effect)と呼ばれる
ものである.
このエネルギー変化の表式(13.2.23)をゲージ不変変数で書き表すこと を考えよう.まず,時間を指定したスケール因子はゲージ依存するので,ゲー ジ不変なスケール因子を作っておく.スケール因子のゲージ変換は
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11