




次へ: 重力不安定性によるゆらぎの成長
上へ: 構造の形成
前へ: 基本方程式
目次
索引
重力は引力のみであり一方的に質量を引き寄せるため,密度ゆらぎがあると,
密度の大きい部分に収縮しようとし,その結果ゆらぎを成長させようとする.
これが重力不安定性によるゆらぎの成長である.だが,この重力による収縮力
を支えてしまうだけの圧力があると,そのゆらぎは成長できなくなる.そこで,
重力不安定となってゆらぎの成長できる条件を定量的に調べてみる.ここで,
最初は空間的なゆらぎが小さいものとして,ゆらぎの一次の項だけを考える線
形化により近似すると,一般の場合に比べて解析が大幅に単純化する.事実,
宇宙の初期ではゆらぎが小さいため,この近似はよい.また,現在でも,大き
なスケールで粗視化してみたゆらぎは小さいため,この場合も線形近似が適用
できる.いま,自己重力系を考え,式(6.1.23)を線形化すると,次式を
得る:
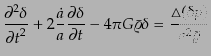 |
(F.2.24) |
ここで,単位質量あたりのエントロピーを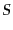 として,この物質の状態方程式
を
として,この物質の状態方程式
を
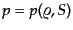 とする.このとき,音速は
とする.このとき,音速は
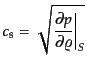 |
(F.2.25) |
で与えられるので,線形近似の範囲内で圧力のゆらぎは
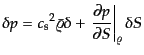 |
(F.2.26) |
となるから,式(6.2.24)は
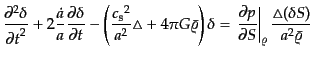 |
(F.2.27) |
と書き直せる.
さてここで,流体の熱伝導が無視できる場合には,流体の流れに沿った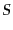 が
保存するので,
が
保存するので,
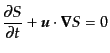 |
(F.2.28) |
が成り立つ.エントロピーの一様等方成分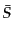 はこの式を満たしている
ことから,この式をゆらぎの成分
はこの式を満たしている
ことから,この式をゆらぎの成分
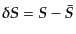 について線形化
すると,
について線形化
すると,
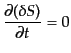 |
(F.2.29) |
となり,エントロピーのゆらぎは時間的に一定であることがわかる.したがっ
て線形近似が成り立つ限り,熱伝導の無視できる流体ではエントロピーゆらぎ
は成長しない.初期条件としてエントロピーのゆらぎがない場合を特に断熱ゆらぎ(adiabatic perturbation)といい,線形成長のあいだ断熱ゆらぎ
は断熱ゆらぎのままである.なんらかの理由で初期に密度ゆらぎと同じオーダー
のエントロピーゆらぎが存在したとしても,通常,式(6.2.27) の右辺
の項は減衰していってしまうので,断熱ゆらぎの場合と同等になっていく.例
えば理想気体の場合,共動体積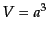 において粒子保存
において粒子保存
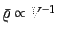 とポアソンの式
とポアソンの式
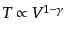 およびマックスウェ
ルの関係式
およびマックスウェ
ルの関係式
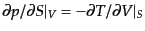 から
から
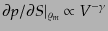 となる.ここで
となる.ここで
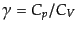 は理想気体の比熱比で,単原子気体のとき
は理想気体の比熱比で,単原子気体のとき
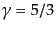 ,
2原子分子気体のとき
,
2原子分子気体のとき
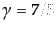 ,多原子分子気体のとき
,多原子分子気体のとき
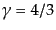 である.したがって,式(6.2.27)の右辺は全体として
である.したがって,式(6.2.27)の右辺は全体として
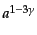 で減衰する.単原子理想気体の場合,
で減衰する.単原子理想気体の場合,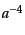 と急速に減衰してしまうことが
わかる.そこで,以降はこの項を無視することにする.
と急速に減衰してしまうことが
わかる.そこで,以降はこの項を無視することにする.
ゆらぎの空間成分をフーリエ分解し,
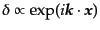 となるモードを考えると,式(6.2.27)は
となるモードを考えると,式(6.2.27)は
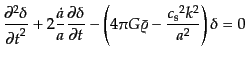 |
(F.2.30) |
となる.この式は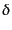 を粒子の位置とみなしたニュートンの運動方程式と
のアナロジーで考えるとおおよそのふるまいがわかる.すなわち,第一項は粒
子の加速を表していて,第二項は速度に比例した抵抗とみなせ,第三項は粒子
の位置の2次関数のポテンシャルからの力とみなせる.つまり,粘性項
を粒子の位置とみなしたニュートンの運動方程式と
のアナロジーで考えるとおおよそのふるまいがわかる.すなわち,第一項は粒
子の加速を表していて,第二項は速度に比例した抵抗とみなせ,第三項は粒子
の位置の2次関数のポテンシャルからの力とみなせる.つまり,粘性項
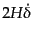 のある,ポテンシャル
のある,ポテンシャル
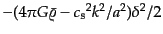 の中での粒子の一次元運動を記述する運動方程式
と等価である.したがって,係数
の中での粒子の一次元運動を記述する運動方程式
と等価である.したがって,係数
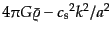 が負ならば下に凸なポテンシャルとなり,
が負ならば下に凸なポテンシャルとなり,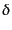 は成長できずに、
振動しながら
は成長できずに、
振動しながら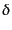 はゼロに近づいていく.これは音速の大きい場合で,圧
力が大きいために重力による収縮力を押し返してしまう状況に対応する.ある
いはスケールが小さい場合で,十分な重力源がない状況ともいえる.逆にこの
係数が正であればポテンシャルは上に凸になり,第二項からの抵抗を感じなが
らではあるが,成長できるようになる.これは,宇宙膨張に引き摺られながら
ではあるが,重力が圧力に打ち勝って収縮をしていく状況である.
はゼロに近づいていく.これは音速の大きい場合で,圧
力が大きいために重力による収縮力を押し返してしまう状況に対応する.ある
いはスケールが小さい場合で,十分な重力源がない状況ともいえる.逆にこの
係数が正であればポテンシャルは上に凸になり,第二項からの抵抗を感じなが
らではあるが,成長できるようになる.これは,宇宙膨張に引き摺られながら
ではあるが,重力が圧力に打ち勝って収縮をしていく状況である.
この係数がちょうどゼロになるような臨界の波数を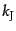 とすると,実
距離にして
とすると,実
距離にして
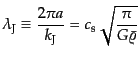 |
(F.2.31) |
を目安とする長さよりも短いスケールのゆらぎは振動してしまって成長できず,
長いスケールのゆらぎは成長できる,ということになる.この臨界の長さ
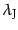 のことをジーンズ長(Jeans length)と呼び,宇宙の
構造形成にとっては非常に重要な量である.また,ジーンズ長のスケールに含
まれる質量に対応する量を考えれば、その質量を持つような物体が重力成長に
より形成されると見ることもできる.具体的には、ジーンズ長を直径とする球
内の質量
のことをジーンズ長(Jeans length)と呼び,宇宙の
構造形成にとっては非常に重要な量である.また,ジーンズ長のスケールに含
まれる質量に対応する量を考えれば、その質量を持つような物体が重力成長に
より形成されると見ることもできる.具体的には、ジーンズ長を直径とする球
内の質量
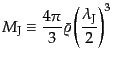 |
(F.2.32) |
をジーンズ質量(Jeans mass)と呼ぶ.ただし,ジーンズ長,ジーンズ質
量などはオーダーを表す量であり,定義によっては前につく因子が上のものと
は異なることもある.
ジーンズ長は時間の関数であり,そのふるまいは音速の時間変化による.例と
して,理想気体の場合のジーンズ長のふるまいを求めてみよう.体積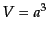 に含まれる気体の質量密度は
に含まれる気体の質量密度は
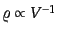 となり,さらにこ
れが断熱変化するとき,ポアソンの式
となり,さらにこ
れが断熱変化するとき,ポアソンの式
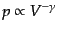 が成り立つ.
したがって,音速は
が成り立つ.
したがって,音速は
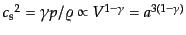 となる.単原子理想気体の場合,共動座
標でみたジーンズ長の時間変化は
となる.単原子理想気体の場合,共動座
標でみたジーンズ長の時間変化は
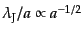 のよ
うに減少していくことになる.質量
のよ
うに減少していくことになる.質量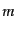 の同種分子でできている理想気体の場
合,音速は
の同種分子でできている理想気体の場
合,音速は
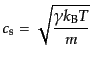 |
(F.2.33) |
で与えられる.非相対論的流体では,
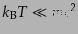 であるから,こ
の音速は光速に比べてずっと小さい.したがって,ジーンズ長はホライズンサ
イズ
であるから,こ
の音速は光速に比べてずっと小さい.したがって,ジーンズ長はホライズンサ
イズ
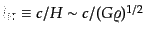 に比べてずっと小さ
くなる.こうして,ホライズンサイズの
に比べてずっと小さ
くなる.こうして,ホライズンサイズの
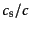 倍より大きなスケー
ルではゆらぎが成長できることになる.
倍より大きなスケー
ルではゆらぎが成長できることになる.





次へ: 重力不安定性によるゆらぎの成長
上へ: 構造の形成
前へ: 基本方程式
目次
索引
All rights reserved © T.Matsubara 2004-2010
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11
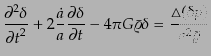
![]() が
保存するので,
が
保存するので,
![]() となるモードを考えると,式(6.2.27)は
となるモードを考えると,式(6.2.27)は
![]() とすると,実
距離にして
とすると,実
距離にして
![]() に含まれる気体の質量密度は
に含まれる気体の質量密度は
![]() となり,さらにこ
れが断熱変化するとき,ポアソンの式
となり,さらにこ
れが断熱変化するとき,ポアソンの式
![]() が成り立つ.
したがって,音速は
が成り立つ.
したがって,音速は
![]() となる.単原子理想気体の場合,共動座
標でみたジーンズ長の時間変化は
となる.単原子理想気体の場合,共動座
標でみたジーンズ長の時間変化は
![]() のよ
うに減少していくことになる.質量
のよ
うに減少していくことになる.質量![]() の同種分子でできている理想気体の場
合,音速は
の同種分子でできている理想気体の場
合,音速は
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11