




次へ: 物質優勢と輻射優勢
上へ: ビッグバン宇宙モデル
前へ: ビッグバン宇宙モデル
目次
索引
十分初期の宇宙では高温状態により熱平衡状態が実現される.そこで,熱平衡
状態の熱力学変数のふるまいについて簡単に見ておく.質量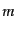 を持つ粒子種
の運動量の大きさ
を持つ粒子種
の運動量の大きさ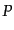 についての分布関数はフェルミ粒子の場合フェルミ・ディ
ラック分布,ボース粒子の場合ボース・アインシュタイン分布で与えられる:
についての分布関数はフェルミ粒子の場合フェルミ・ディ
ラック分布,ボース粒子の場合ボース・アインシュタイン分布で与えられる:
![$\displaystyle f({\mbox{\boldmath$P$}}) = \frac{1}{ \displaystyle \exp\left[\frac{E({\mbox{\boldmath$P$}}) - \mu}{k_{\rm B}T}\right]\pm 1}$](img447.png) |
(D.1.1) |
ここで,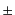 符号はフェルミ粒子の場合
符号はフェルミ粒子の場合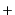 ,ボース粒子の場合
,ボース粒子の場合 に対応す
る.また,
に対応す
る.また,
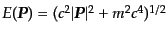 は粒子のエネ
ルギー,
は粒子のエネ
ルギー,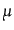 は化学ポテンシャルである.
は化学ポテンシャルである.
統計力学によれば,熱力学変数はこの分布関数に重みをつけて運動量
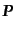 で積分することにより得られる.数密度
で積分することにより得られる.数密度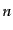 についてはそのまま,エ
ネルギー密度
についてはそのまま,エ
ネルギー密度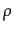 については粒子のエネルギー,圧力
については粒子のエネルギー,圧力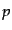 については単位面
積を横切る粒子の運動量流束,がそれぞれ重みとなる.すなわち,
については単位面
積を横切る粒子の運動量流束,がそれぞれ重みとなる.すなわち,
と表される.ここで,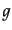 は考えている粒子の内部自由度であり,スピン自由
度などがそれにあたる.
は考えている粒子の内部自由度であり,スピン自由
度などがそれにあたる.
上の表式はそのままでは積分が残っているため,そのふるまいが見にくい.粒
子が相対論的あるいは非相対論的な極限で十分よく近似できる状態になってい
る場合にはもっと簡単な形となる.まず,非相対論的な極限
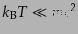 では
では
となる.粒子の平均運動エネルギーが粒子の質量エネルギーを下回ると指数関
数的に粒子数が急減することになり,したがってエネルギー密度と圧力も同様
に減る.これは,平均的に粒子が非相対論的であれば,対生成によって粒子数
を増やすことがほとんどできなくなり,消滅が一方的に進むことによるもので
ある.
次に,相対論的な極限
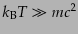 を考える.ここでは化学ポテン
シャルが粒子の平均運動エネルギーに比べて無視できる
を考える.ここでは化学ポテン
シャルが粒子の平均運動エネルギーに比べて無視できる
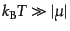 の場合を考えると次のようになる:
の場合を考えると次のようになる:
ここで,
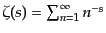 , (
, (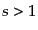 )はリーマン・ツェー
タ関数であり,その
)はリーマン・ツェー
タ関数であり,その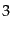 における値は
における値は
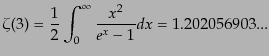 |
(D.1.11) |
である.
非相対論的粒子のエネルギー密度は相対論的粒子に比べると指数関数的に小さ
なものとなっているため,熱平衡状態であるかぎり,宇宙全体でのエネルギー
密度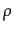 への寄与としてはほとんどすべて相対論的粒子のもの
への寄与としてはほとんどすべて相対論的粒子のもの
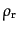 によって担われているということに
なる:
によって担われているということに
なる:
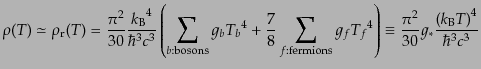 |
(D.1.12) |
ここで,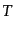 は光子の温度であり,宇宙の温度を代表するものである.そのほ
かの相対論的粒子の温度
は光子の温度であり,宇宙の温度を代表するものである.そのほ
かの相対論的粒子の温度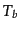 ,
, 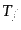 などは光子と平衡状態にあ
れば光子の温度と同一であるが,光子との相互作用が切れている場合には一般
に異なっている.上式の
などは光子と平衡状態にあ
れば光子の温度と同一であるが,光子との相互作用が切れている場合には一般
に異なっている.上式の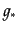 は有効自由度と呼ばれるもので,いまの近似で
は,全相対論的粒子について,以下のように重みつきで平均した
は有効自由度と呼ばれるもので,いまの近似で
は,全相対論的粒子について,以下のように重みつきで平均した
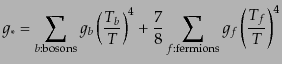 |
(D.1.13) |
で与えられる.
後に見るように,現在のニュートリノは光子と相互作用がなく,その温度は光
子の温度に比べて
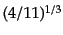 倍だけ小さい.また,光子の自由度は2,相
対論的ニュートリノの自由度は一種類あたり2である.現在の相対論的ニュー
トリノの種類を3とすれば,有効自由度の現在値は,
倍だけ小さい.また,光子の自由度は2,相
対論的ニュートリノの自由度は一種類あたり2である.現在の相対論的ニュー
トリノの種類を3とすれば,有効自由度の現在値は,
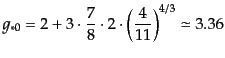 |
(D.1.14) |
である.電子と陽電子の対消滅の起こる
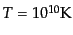 以後は相対論的
粒子の数に変化はないため,その時点まで時間を遡ってもこの値が保たれてい
る.それ以前には相対論的粒子の種類が増えるので,これよりも大きな数とな
る.
以後は相対論的
粒子の数に変化はないため,その時点まで時間を遡ってもこの値が保たれてい
る.それ以前には相対論的粒子の種類が増えるので,これよりも大きな数とな
る.
次に宇宙のエントロピーのふるまいを調べてみよう.以前述べたように,宇宙
のエントロピーはよい近似で保存するため重要である.熱力学によると一般に,
内部エネルギー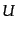 ,体積
,体積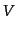 ,粒子数
,粒子数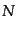 を持つ開いた系のエントロピー
を持つ開いた系のエントロピー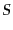 は,
は,
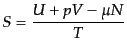 |
(D.1.15) |
で与えられる.単位体積あたりのエントロピーとして,エントロピー密度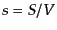 を定義し,粒子の数密度を
を定義し,粒子の数密度を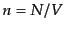 とすると,
とすると,
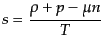 |
(D.1.16) |
である.
式(3.1.15)で見たように,化学ポテンシャルが粒
子の熱エネルギーに比べて無視できる(
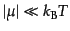 )か,あるい
は共動体積あたりの粒子数が保存する(
)か,あるい
は共動体積あたりの粒子数が保存する(
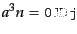 )か,どちらがが
満たされる場合には共動体積あたりのエントロピーは一定となることがわかる.
現実の宇宙では,化学ポテンシャルは重要でないことがほとんどであり,宇宙
のエントロピーは保存する.
)か,どちらがが
満たされる場合には共動体積あたりのエントロピーは一定となることがわかる.
現実の宇宙では,化学ポテンシャルは重要でないことがほとんどであり,宇宙
のエントロピーは保存する.
エネルギー密度の場合と同様に,エントロピーへの非相対論的粒子の寄与もま
た無視できる.相対論的粒子においては式(4.1.10),つまり,
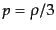 であるから,粒子種あたり
であるから,粒子種あたり
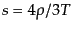 となる.したがっていまの
近似では,全相対論的粒子のエントロピーを足し合わせることにより
となる.したがっていまの
近似では,全相対論的粒子のエントロピーを足し合わせることにより
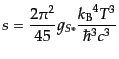 |
(D.1.17) |
となる.ここで,エントロピーについての有効自由度は
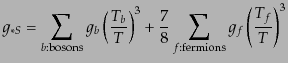 |
(D.1.18) |
である.相対論的ニュートリノが3種類の場合の現在の値は
 |
(D.1.19) |
である.エントロピーの保存
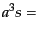 一定
より,式(4.1.17)か
ら,
一定
より,式(4.1.17)か
ら,
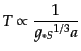 |
(D.1.20) |
であることがわかる.つまり,有効自由度があまり変化しなければ,宇宙の温
度はスケール因子に反比例して冷却する.温度が冷却するとそれまで相対論的
であった粒子が非相対論的になったり,他の粒子と結合するなどして,有効自
由度が小さくなる時期がある.そのような時期には温度の冷却が単純なスケー
ル因子の反比例関係よりも多少鈍ることになる.つまり,それまで多くの粒子
種によって担われていたエントロピーが,より少ない粒子種だけで担わなけれ
ばならなくなることにより,流入してくる.そのエントロピーが温度の低下を
鈍らせることになるのである.
宇宙の温度はスケール因子の増大とともに,以上のように冷却していくため,
宇宙の中の物質状態はさまざまに変化して行くことになる.





次へ: 物質優勢と輻射優勢
上へ: ビッグバン宇宙モデル
前へ: ビッグバン宇宙モデル
目次
索引
All rights reserved © T.Matsubara 2004-2010
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11
![]() を持つ粒子種
の運動量の大きさ
を持つ粒子種
の運動量の大きさ![]() についての分布関数はフェルミ粒子の場合フェルミ・ディ
ラック分布,ボース粒子の場合ボース・アインシュタイン分布で与えられる:
についての分布関数はフェルミ粒子の場合フェルミ・ディ
ラック分布,ボース粒子の場合ボース・アインシュタイン分布で与えられる:
![]() で積分することにより得られる.数密度
で積分することにより得られる.数密度![]() についてはそのまま,エ
ネルギー密度
についてはそのまま,エ
ネルギー密度![]() については粒子のエネルギー,圧力
については粒子のエネルギー,圧力![]() については単位面
積を横切る粒子の運動量流束,がそれぞれ重みとなる.すなわち,
については単位面
積を横切る粒子の運動量流束,がそれぞれ重みとなる.すなわち,
![]() では
では
![]() を考える.ここでは化学ポテン
シャルが粒子の平均運動エネルギーに比べて無視できる
を考える.ここでは化学ポテン
シャルが粒子の平均運動エネルギーに比べて無視できる
![]() の場合を考えると次のようになる:
の場合を考えると次のようになる:
![]() への寄与としてはほとんどすべて相対論的粒子のもの
への寄与としてはほとんどすべて相対論的粒子のもの
![]() によって担われているということに
なる:
によって担われているということに
なる:
![]() 倍だけ小さい.また,光子の自由度は2,相
対論的ニュートリノの自由度は一種類あたり2である.現在の相対論的ニュー
トリノの種類を3とすれば,有効自由度の現在値は,
倍だけ小さい.また,光子の自由度は2,相
対論的ニュートリノの自由度は一種類あたり2である.現在の相対論的ニュー
トリノの種類を3とすれば,有効自由度の現在値は,
![]() ,体積
,体積![]() ,粒子数
,粒子数![]() を持つ開いた系のエントロピー
を持つ開いた系のエントロピー![]() は,
は,
![]() であるから,粒子種あたり
であるから,粒子種あたり
![]() となる.したがっていまの
近似では,全相対論的粒子のエントロピーを足し合わせることにより
となる.したがっていまの
近似では,全相対論的粒子のエントロピーを足し合わせることにより
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11