




次へ: 赤方偏移
上へ: ロバートソン・ウォーカー計量
前へ: 宇宙原理
目次
索引
空間の計量は一様等方空間の場合,時間に依存する定数倍を除いて式
(2.2.15)により決まってしまうので,ワイルの要請と宇宙原理を同時に満
たす計量は
![$\displaystyle ds^2 = -c^2 dt^2 + a^2(t) \left[ \frac{dr^2}{1 - K r^2} + r^2 \left(d\theta^2 + \sin^2\theta d\phi^2\right) \right]$](img111.png) |
(B.3.17) |
となる.これをロバートソン・ウォーカー計量 (RW計量)と呼ぶ.この
計量は宇宙論において最も重要なものの一つである.空間のスケールを決める
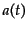 はスケール因子(scale factor)というもので,空間の膨張や収縮を表わ
すことになる.また,曲率
はスケール因子(scale factor)というもので,空間の膨張や収縮を表わ
すことになる.また,曲率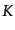 は一般に時間変化をしてもよいが,その場合で
も動径座標
は一般に時間変化をしてもよいが,その場合で
も動径座標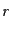 の再定義をすれば結局スケール因子の時間変化にくりこまれる
ので,一般性を失なわずに
の再定義をすれば結局スケール因子の時間変化にくりこまれる
ので,一般性を失なわずに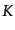 は定数であるとしてよい.このときの定数とし
て,現在時刻
は定数であるとしてよい.このときの定数とし
て,現在時刻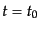 の曲率を採用すれば,現在時刻でのスケール因子は
の曲率を採用すれば,現在時刻でのスケール因子は
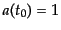 という規格化をもつことになる.以下ではこの規格化を用いるこ
ととする.
という規格化をもつことになる.以下ではこの規格化を用いるこ
ととする.
上の形は球面の面積で定義される動径座標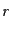 によって表示されるものである
が,動径座標の定義を変えることにより,他の形にも書き
表わすことができる.まず,次の変数変換
によって表示されるものである
が,動径座標の定義を変えることにより,他の形にも書き
表わすことができる.まず,次の変数変換
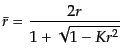 |
(B.3.18) |
により,ロバートソン・ウォーカー計量は
![$\displaystyle ds^2 = -c^2 dt^2 + \frac{a^2(t)}{\displaystyle\left(1 + \frac{K}{...
...t[ d\bar{r}^2 + \bar{r}^2 \left(d\theta^2 + \sin^2\theta d\phi^2\right) \right]$](img116.png) |
(B.3.19) |
という形となる.この形から,RW計量は共形変換
(conformal transformation)
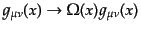 により平坦な空間の計量と同じ形となるという
性質を持っていることがわかる.
により平坦な空間の計量と同じ形となるという
性質を持っていることがわかる.
スケール因子が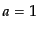 のとき,実際の測地的距離
のとき,実際の測地的距離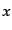 は動径座標
は動径座標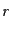 と
と
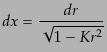 |
(B.3.20) |
の関係にあるので,これを積分して得られる関数を
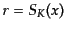 とすると
とすると
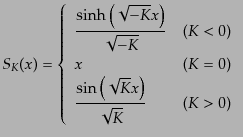 |
(B.3.21) |
である.上の規格化ではこれは現在の宇宙での測地的距離を表している.した
がってRW計量は
![$\displaystyle ds^2 = -c^2 dt^2 + a^2(t) \left[ dx^2 + {S_K}^2(x) \left(d\theta^2 + \sin^2\theta d\phi^2\right) \right]$](img122.png) |
(B.3.22) |
という形にも表わすことができる.物質素片に固定された点は,原点からの測
地的距離がスケール因子に比例して増えていく.この座標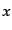 は
は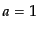 となると
きの,実際の測地的距離である.これを共動距離(comoving distance)という.
となると
きの,実際の測地的距離である.これを共動距離(comoving distance)という.
さて,上で採用した
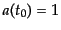 とは異なる規格化もまた広く使われることが
あるので,ここでコメントしておく.曲率がゼロでないとき,座標
とは異なる規格化もまた広く使われることが
あるので,ここでコメントしておく.曲率がゼロでないとき,座標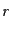 に曲率
に曲率
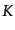 の値による再定義
の値による再定義
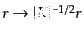 を行なえば,
を行なえば,
![$\displaystyle ds^2 = -c^2 dt^2 + R^2(t) \left[ \frac{dr^2}{1 - k r^2} + r^2 \left(d\theta^2 + \sin^2\theta d\phi^2\right) \right]$](img124.png) |
(B.3.23) |
となる.ここで,
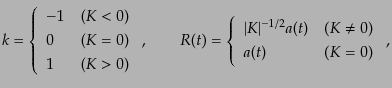 |
(B.3.24) |
である.曲率がゼロでない場合には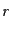 は無次元化していて,曲率は離散的な
値,
は無次元化していて,曲率は離散的な
値,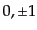 のみをとる.さらにスケール因子
のみをとる.さらにスケール因子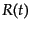 は長さの次元を持つ.
したがって単位系を再定義しない限り現在値を
は長さの次元を持つ.
したがって単位系を再定義しない限り現在値を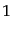 に規格化することができな
い.それは
に規格化することができな
い.それは
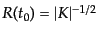 となり,曲率のスケールはスケール因子の
現在値を通して入ってくることになる.このような規格化を用いる場合には注
意すべき事項である.
となり,曲率のスケールはスケール因子の
現在値を通して入ってくることになる.このような規格化を用いる場合には注
意すべき事項である.





次へ: 赤方偏移
上へ: ロバートソン・ウォーカー計量
前へ: 宇宙原理
目次
索引
All rights reserved © T.Matsubara 2004-2010
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11
![$\displaystyle ds^2 = -c^2 dt^2 + a^2(t) \left[ \frac{dr^2}{1 - K r^2} + r^2 \left(d\theta^2 + \sin^2\theta d\phi^2\right) \right]$](img111.png)
![]() によって表示されるものである
が,動径座標の定義を変えることにより,他の形にも書き
表わすことができる.まず,次の変数変換
によって表示されるものである
が,動径座標の定義を変えることにより,他の形にも書き
表わすことができる.まず,次の変数変換
![]() のとき,実際の測地的距離
のとき,実際の測地的距離![]() は動径座標
は動径座標![]() と
と
![]() とは異なる規格化もまた広く使われることが
あるので,ここでコメントしておく.曲率がゼロでないとき,座標
とは異なる規格化もまた広く使われることが
あるので,ここでコメントしておく.曲率がゼロでないとき,座標![]() に曲率
に曲率
![]() の値による再定義
の値による再定義
![]() を行なえば,
を行なえば,
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11