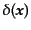 の値の空間的
な分布がガウス分布にしたがう.すなわち,空間のある点における密度ゆらぎ
の値が
の値の空間的
な分布がガウス分布にしたがう.すなわち,空間のある点における密度ゆらぎ
の値が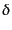 から
から
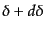 の微小区間内にある確率は
の微小区間内にある確率は
ゆらぎは空間の点ごとにランダムに変化する変数で表される.一般にゆらぎは 統計的な性質によりその特徴を定量的に記述される.さまざ まな物理現象に対して,一般的によく表れてくる統計的性質にガウシアンゆら ぎというものがある.通常のモ デルでは宇宙初期の密度ゆらぎもガウシアンゆらぎの性質を持っていると考え られている.以下に見るように,ゆらぎの重力成長が線形領域にある限りその ガウシアン性は保たれる.このガウシアン密度ゆらぎの統計的な性質を調べる ことで,構造形成が全体としてどう進むのかを議論することができる.
ガウシアン密度ゆらぎにおいては,密度ゆらぎ
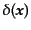 の値の空間的
な分布がガウス分布にしたがう.すなわち,空間のある点における密度ゆらぎ
の値が
の値の空間的
な分布がガウス分布にしたがう.すなわち,空間のある点における密度ゆらぎ
の値が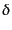 から
から
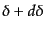 の微小区間内にある確率は
の微小区間内にある確率は
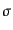 は密度ゆらぎの分散
は密度ゆらぎの分散
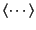 は空間的な平均値を表している.
は空間的な平均値を表している.
このガウス分布は,ランダムな要素を含むさまざまな物理現象においてよく表 れてくるもので,一般的に重要な分布である.この分布が普遍的によく表れる 理由の一つは中心極限定理というもので説明される.一般に多数の独立なラン ダム変数があるとき,それらのランダム変数の和もひとつのランダム変数であ る.中心極限定理によれば,もともとのランダム変数がどのような分布を持っ ていようともその和の分布はガウス分布となるのである.
インフレーションモデルによって生成される密度ゆらぎも通常のモデルではほ ぼガウシアン密度ゆらぎとなる.また,観測的にも宇宙背景放射のゆらぎ や宇宙大規模構造を調べることにより,宇宙の初期ゆらぎはほぼガウス分布で 説明できることが知られている.このため,よい近似で初期ゆらぎはガウシア ン統計にしたがうと考えられているのである.
初期ゆらぎがガウシアン統計にしたがうならば,密度ゆらぎが線形領域にある
限り重力成長しても依然ガウシアン統計にしたがう.線形領域では空間の各点
におけるゆらぎは
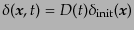 で
与えられるので,分布関数(16.5.31)の形はそのまま成り立つ
ことがわかる.ただし,ゆらぎの分散
で
与えられるので,分布関数(16.5.31)の形はそのまま成り立つ
ことがわかる.ただし,ゆらぎの分散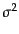 は
は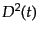 に比例して時間変化
する.
に比例して時間変化
する.
密度ゆらぎの線形成長解を球対称モデルにより非線形領域まで外挿し、天体形 成を解析的に記述するモデルが考えられている.一般にゆらぎは球対称ではな いのであるが,ある時期に形成される天体の数密度を見積もるのにこのモデル が用いられ,現象論的によいモデルであることが知られている.これはプレス・ シェヒター理論と呼ばれ,宇宙論的な構造形成理論において広く用いられてい る.
質量が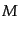 から
から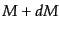 の間にあるような天体の,単位体積あたりの数密度
を
の間にあるような天体の,単位体積あたりの数密度
を とするとき,この
とするとき,この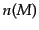 を質量関数という.プレス・シェヒター理
論はこの関数を解析的に求めるモデルである.まず,ある点のまわり
に半径
を質量関数という.プレス・シェヒター理
論はこの関数を解析的に求めるモデルである.まず,ある点のまわり
に半径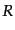 の球を考えると,ゆらぎが小さい場合その球の内部に存在する質量
は
の球を考えると,ゆらぎが小さい場合その球の内部に存在する質量
は
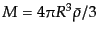 である.このように半径と質量が対応し,その球
の内部で密度ゆらぎを平均した量を質量スケール
である.このように半径と質量が対応し,その球
の内部で密度ゆらぎを平均した量を質量スケール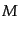 のゆらぎ
のゆらぎ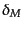 という.
ガウシアンゆらぎでは,このような平均操作した量もガウシアン統計にしたが
うので,その分布関数は
という.
ガウシアンゆらぎでは,このような平均操作した量もガウシアン統計にしたが
うので,その分布関数は
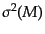 は平均されたゆらぎ
は平均されたゆらぎ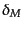 の分散であ
る.
の分散であ
る.
十分初期のある一点に存在する物質素片が時間発展とともにどうなるかという
ことを考える.プレス・シェヒター理論では,その点において線形成長解から
求めた質量スケール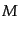 のゆらぎ
のゆらぎ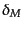 がある値
がある値
 を越えた
とき,近くに質量
を越えた
とき,近くに質量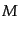 の天体が形成され,その物質素片はその天体の一部として
取り込まれると考える.この臨界値
の天体が形成され,その物質素片はその天体の一部として
取り込まれると考える.この臨界値
 は,
式(16.3.18)で与えられる球対称モデルの崩壊点を与える線形ゆらぎの
値
は,
式(16.3.18)で与えられる球対称モデルの崩壊点を与える線形ゆらぎの
値
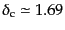 が通常用いられる.この臨界値を越える領
域P2の
割合は質量スケールの関数として
が通常用いられる.この臨界値を越える領
域P2の
割合は質量スケールの関数として
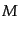 よりも大きな天体へ取り込まれた物質の量は,単位
体積あたり
よりも大きな天体へ取り込まれた物質の量は,単位
体積あたり
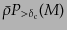 である.ここで,質量
が
である.ここで,質量
が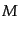 から
から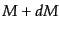 の間に形成された天体に取り込まれる単位体積あたりの物質の
質量は
の間に形成された天体に取り込まれる単位体積あたりの物質の
質量は
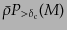 と
と
 の差で与えられるが,この量は質量関数を用いて
の差で与えられるが,この量は質量関数を用いて とも
書くことができる.ただしここでは一度形成された天体がより大きな天体にさ
らに取り込まれるというプロセスを無視しているP3.
また,このままの考え方では,もともとゆらぎが負、
すなわち密度が平均密度よりも低い領域にある質量素片はいつまでたっても天
体に取り込まれないことになってしまう.時間が十分経過して
とも
書くことができる.ただしここでは一度形成された天体がより大きな天体にさ
らに取り込まれるというプロセスを無視しているP3.
また,このままの考え方では,もともとゆらぎが負、
すなわち密度が平均密度よりも低い領域にある質量素片はいつまでたっても天
体に取り込まれないことになってしまう.時間が十分経過して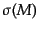 が十
分に大きくなる極限で式(16.5.34)は
が十
分に大きくなる極限で式(16.5.34)は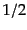 に近づく.これでは,
宇宙に存在する物質の半分は永遠に天体形成に寄与しない.プレス・シェヒター
理論では,上のように見積もられる天体形成に取り込まれる質量を,単に2倍す
るという処方で,この問題を回避する.こうして,
に近づく.これでは,
宇宙に存在する物質の半分は永遠に天体形成に寄与しない.プレス・シェヒター
理論では,上のように見積もられる天体形成に取り込まれる質量を,単に2倍す
るという処方で,この問題を回避する.こうして,
簡単な場合として,ゆらぎの分散が巾乗の形
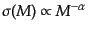 で与えられるときを考えてみる.これはゆらぎのパワースペクト
ルが巾乗の形
で与えられるときを考えてみる.これはゆらぎのパワースペクト
ルが巾乗の形
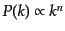 で与えられる場合に対応し,そのべき指数の
関係は式(6.6.135)と同様の関係により,
で与えられる場合に対応し,そのべき指数の
関係は式(6.6.135)と同様の関係により,
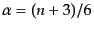 となる.
このとき,式(16.5.36)の質量関数の形は
となる.
このとき,式(16.5.36)の質量関数の形は
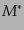 は
は
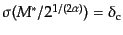 で定義
される質量であり,これより大きな質量の天体の数は指数関数的に少なくなっ
ていることがわかる.
で定義
される質量であり,これより大きな質量の天体の数は指数関数的に少なくなっ
ていることがわかる.
プレス・シェヒター理論によると線形理論の外挿によって,非線形な天体形成
を現象論的に扱うことができる.特に銀河や銀河団の形成を調べる解析的なモ
デルとして広く使われている.プレス・シェヒター理論により予言される天体
形成率は時間的な発展も含めて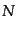 体シミュレーションと比較してもよい一致を
示す.上に述べたようにプレス・シェヒター理論には理論的に正当性の明らか
ではない処方をいくつか含んでいる.このため,この理論を信頼して使うこと
のできる理由は,
体シミュレーションと比較してもよい一致を
示す.上に述べたようにプレス・シェヒター理論には理論的に正当性の明らか
ではない処方をいくつか含んでいる.このため,この理論を信頼して使うこと
のできる理由は,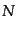 体シミュレーションの結果をよく再現するというところ
にある.
体シミュレーションの結果をよく再現するというところ
にある.
我々は宇宙の物質のうち,銀河などとして光っているものしか観測できない. だが、宇宙の物質のほとんどはダークマターであって光を放たない.光を放ち 得るバリオンのうち,実際に銀河などとして光っているものはさらにわずかで ある.すると,銀河分布を用いて宇宙の大規模構造を観測しても,それがその ままダークマターを含む物質全体の分布を表しているとは限らない.我々の知 りたいのはむしろ物質全体の分布の方である.銀河の数密度が物質密度に単純 に比例するならば,銀河分布を測定すれば十分である.だが,銀河の形成が複 雑な非線形過程である以上,一般にはそのような比例関係は成り立たないと考 えられる.とはいえ,銀河は物質密度のゆらぎを種にして形成されたのである から,銀河分布と物質分布の間に何の関係もないということはない.この意味 で,銀河分布は物質分布のバイアスされた(すなわち偏りのある)トレーサー であるということができるのである.このようなバイアスがどのようなもので あるのかは銀河形成過程がどのようなものであるかを知らなければわからない. だが現在のところ,完全な非線形過程である銀河の形成についてよくわかって いるとはいいがたい.
銀河形成を現象論的に表す簡単なものとして,密度が局所的に極大になって いるピークの位置に銀河が形成されるという簡単なモデルを考える.この ようなモデルをピークモデルという(図16.2).
ここで,密度の低い場所でピークになっていても銀河は形成されず,密度ゆら ぎがあるしきい値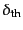 よりも大きな場所にあるピークのみが銀
河になるとするモデルがよく考えられる.さらに,ピークを求める前に密度場
をある決まったスケール
よりも大きな場所にあるピークのみが銀
河になるとするモデルがよく考えられる.さらに,ピークを求める前に密度場
をある決まったスケール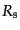 でならしてからピークを求める.そうで
なければ小さなスケールのゆらぎがたくさんのピークを作ってしまうからであ
る.このときのスケール
でならしてからピークを求める.そうで
なければ小さなスケールのゆらぎがたくさんのピークを作ってしまうからであ
る.このときのスケール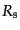 をスムージングスケールという.
をスムージングスケールという.
ピークモデルを直感的にとらえるため,密度ゆらぎを地形に例えてみよう.す ると密度の大きい部分が山,小さい部分が谷となる.この場合,あるしきい値 となる標高よりも高い位置に存在する山の頂の部分が天体形成の場所に対応す る.
このピークモデルは銀河の形成を表すだけでなく,銀河団など他の天体の形成
を表すモデルと考えてもよい.このモデルにおいては,2つのパラメータ
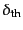 ,
, 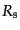 があるが,これらの値は考えている天体に応
じて現象論的に決められる.スムージングスケール
があるが,これらの値は考えている天体に応
じて現象論的に決められる.スムージングスケール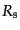 としては,対応する天体の典型的な質量スケールが
としては,対応する天体の典型的な質量スケールが
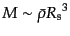 となるように決めるのが自然である.また,しき
い値
となるように決めるのが自然である.また,しき
い値
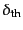 はその天体の数密度を再現するように決められる.この
ようにしてパラメータを決定すると,与えられた密度ゆらぎのパワースペクト
ルからピークがどのような統計にしたがうかが決まる.
はその天体の数密度を再現するように決められる.この
ようにしてパラメータを決定すると,与えられた密度ゆらぎのパワースペクト
ルからピークがどのような統計にしたがうかが決まる.
一般には,任意のゆらぎからピークの統計を導くことは
数学的に複雑な問題である.だが,スムージングスケールよりも十分長いスケー
ルで,かつ密度ゆらぎがガウシアン統計にしたがう線形領域の極限ではその関
係は比較的単純な形になることが知られている.この極限では,
密度ゆらぎのパワースペクトル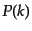 が与えられたとき,ピーク数密度の空間
的ゆらぎから求めたパワースペクトル
が与えられたとき,ピーク数密度の空間
的ゆらぎから求めたパワースペクトル
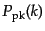 は近似的に
は近似的に
 はパワースペクトル
はパワースペクトル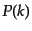 とピークを決める
パラメータ
とピークを決める
パラメータ
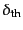 ,
, 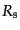 から決まる.具体的には,スケー
ル
から決まる.具体的には,スケー
ル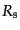 でならされた密度ゆらぎの分散
でならされた密度ゆらぎの分散
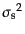 を用いて
を用いて
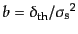 で与えられる.この関係式
(16.5.38)は密度ゆらぎ
で与えられる.この関係式
(16.5.38)は密度ゆらぎ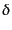 とピークの数密度のゆらぎ
とピークの数密度のゆらぎ
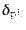 が
が
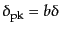 のように比例する
線形バイアスモデルと呼ばれるものでも成り立つ.この意味で
のように比例する
線形バイアスモデルと呼ばれるものでも成り立つ.この意味で はバイアス
パラメータと呼ばれる.ここで考えているピークモデルは厳密には線形バイア
スではないが,線形領域では近似的に線形バイアスに近いものになるのである.
はバイアス
パラメータと呼ばれる.ここで考えているピークモデルは厳密には線形バイア
スではないが,線形領域では近似的に線形バイアスに近いものになるのである.
式(16.5.38)から,しきい値
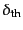 が大きければ大きいほど,ピークのパワースペクトルはもとの密度ゆらぎのそ
れに対して増幅されることがわかる.さきほどの地形との対応でいうならば,
高い山の頂というのは,富士山のように孤立して存在することはまれで,アル
プス地方に見られるようにいくつもの頂が近くに群れ集まることのほうが多い.
すなわちピークの数密度の空間的ゆらぎがより大きくなるのである.しきい
値
が大きければ大きいほど,ピークのパワースペクトルはもとの密度ゆらぎのそ
れに対して増幅されることがわかる.さきほどの地形との対応でいうならば,
高い山の頂というのは,富士山のように孤立して存在することはまれで,アル
プス地方に見られるようにいくつもの頂が近くに群れ集まることのほうが多い.
すなわちピークの数密度の空間的ゆらぎがより大きくなるのである.しきい
値
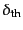 が大きければ大きいほどその増幅率は大きくなる.
が大きければ大きいほどその増幅率は大きくなる.
実際に,銀河の数密度のゆらぎよりも銀河団の数密度のゆらぎの方が大きいこ とが知られている.これは銀河団が銀河分布のピークに対応していると考え ればこのピークモデルである程度説明できる.また,明るい銀河の数密度のゆ らぎは暗い銀河の数密度のゆらぎに比べて大きいことが知られている.これは 明るい銀河ほどまれな天体であり,大きなしきい値を持つので,ゆらぎがより 大きく増幅されると考えることにより,ピークモデルである程度理解できる.
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11