




次へ: 球面調和関数
上へ: 特殊関数
前へ: デルタ関数
目次
索引
最初のいくつかの値:
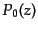 |
 |
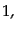 |
(C.2.1) |
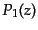 |
 |
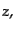 |
(C.2.2) |
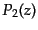 |
 |
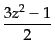 |
(C.2.3) |
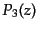 |
 |
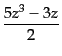 |
(C.2.4) |
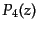 |
 |
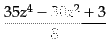 |
(C.2.5) |
巾乗をルジャンドル多項式で表すと次のようになる:
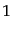 |
 |
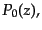 |
(C.2.6) |
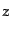 |
 |
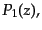 |
(C.2.7) |
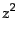 |
 |
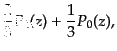 |
(C.2.8) |
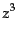 |
 |
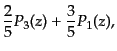 |
(C.2.9) |
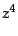 |
 |
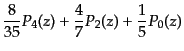 |
(C.2.10) |
直交性と完全性:
| |
|
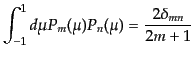 |
(C.2.11) |
| |
|
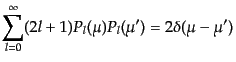 |
(C.2.12) |





次へ: 球面調和関数
上へ: 特殊関数
前へ: デルタ関数
目次
索引
All rights reserved © T.Matsubara 2004-2010
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11
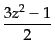
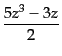
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11