




次へ: キュムラント展開定理
上へ: 天体分布の統計理論
前へ: 天体分布の相関関数とパワースペクトル
目次
索引
Subsections
高次相関関数
天体分布の高次相関関数
銀河の相関関数
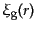 は天体分布の分布を特徴づける一つの量であ
るが,この中に分布の統計的情報がすべて含まれているわけではない.銀河の
相関関数は2つの微小体積中に同時に銀河が存在する確率から定義することが
できた.その意味で,これは2点相関関数とも呼ばれる.これを拡張して,3つ
の微小体積
は天体分布の分布を特徴づける一つの量であ
るが,この中に分布の統計的情報がすべて含まれているわけではない.銀河の
相関関数は2つの微小体積中に同時に銀河が存在する確率から定義することが
できた.その意味で,これは2点相関関数とも呼ばれる.これを拡張して,3つ
の微小体積
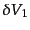 ,
,
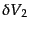 ,
,
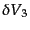 に同時に銀河が存在す
る確率
に同時に銀河が存在す
る確率
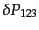 から銀河の3点相関関数
から銀河の3点相関関数
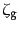 が次のように
定義される:
が次のように
定義される:
![$\displaystyle \delta P_{123} = \bar{n}^3 \delta V_1 \delta V_2 \delta V_3 \left...
... g}(r_{13}) + \xi_{\rm g}(r_{23}) + \zeta_{\rm g}(r_{12},r_{13},r_{23}) \right]$](img4426.png) |
(O.2.27) |
この定義において,3点相関関数
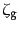 以外のものが足されている理
由は以下の通りである.すなわち,もし3点がお互いに無限に離れていればこ
の確率は第1項のみとなる.また,点3が無限の彼方にある場合には点1と点2の
2点相関関数によりこの確率が定まり,第2項までで与えられる.同様にどれか
1点が無限の彼方にある場合は第4項まででこの確率が与えられる.したがって,
3点がお互いに影響し合う場合にはじめて3点相関関数が効果を発揮するように
定義されていることがわかるであろう.
以外のものが足されている理
由は以下の通りである.すなわち,もし3点がお互いに無限に離れていればこ
の確率は第1項のみとなる.また,点3が無限の彼方にある場合には点1と点2の
2点相関関数によりこの確率が定まり,第2項までで与えられる.同様にどれか
1点が無限の彼方にある場合は第4項まででこの確率が与えられる.したがって,
3点がお互いに影響し合う場合にはじめて3点相関関数が効果を発揮するように
定義されていることがわかるであろう.
より高次の相関関数も同様に定義される.4点相関関数
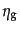 は4つの
微小体積中に銀河が存在する確率により定義される:
は4つの
微小体積中に銀河が存在する確率により定義される:
| |
|
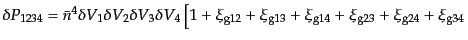 |
|
| |
|
![$\displaystyle \quad\left. +\;
\xi_{\rm g12} \xi_{\rm g34} +
\xi_{\rm g13} \xi...
...a_{\rm g124} + \zeta_{\rm g134} +
\zeta_{\rm g234} + \eta_{\rm g1234}
\right]$](img4429.png) |
(O.2.28) |
ここで,
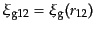 などのように略記した.
ここで,多数の項は4点の部分集合のあらゆる可能な取り方に対応している.
などのように略記した.
ここで,多数の項は4点の部分集合のあらゆる可能な取り方に対応している.
このように,多点での存在確率をあらゆる可能な部分集合の取り方に対応した
相関関数で展開することを,クラスター展開 (cluster expansion)と呼
ぶ.2点{1,2} の可能な部分集合の取り方は{{1},{2}}, {{1,2}}
であり,2点相関関数の定義式(15.1.4)の2項に対応する.3点
{1,2,3}の展開は{{1},{2},{3}}, {{1,2},{3}},
{{1,3},{2}}, {{2,3},{1}}, {{1,2,3}}となり,式
(15.2.27)の各項に対応する.4点相関関数の場合,あるいはより高次
の場合も同様である.
高次相関関数の階層モデル
銀河分布について,高次相関関数を2点相関関数で表されるとしてモデル化さ
れる場合がある.特に,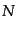 点相関関数が
点相関関数が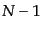 個の2点相関関数の積を組み合
わせたもので表されるようなモデルをを階層モデル (Hierarchical
model)と呼ぶ.この場合,対称性からその形はある程度決まるが,未定の定
数が含まれることになる.例えば,3点相関関数は
個の2点相関関数の積を組み合
わせたもので表されるようなモデルをを階層モデル (Hierarchical
model)と呼ぶ.この場合,対称性からその形はある程度決まるが,未定の定
数が含まれることになる.例えば,3点相関関数は
![$\displaystyle \zeta_{\rm g123} = Q \left[\xi_{\rm g12}\xi_{\rm g23} + \xi_{\rm g23}\xi_{\rm g31} + \xi_{\rm g31}\xi_{\rm g12} \right]$](img4432.png) |
(O.2.29) |
と表される.ここで,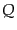 は未定の定数であり,モデルパラメータとなる.ま
た,4点相関関数は
は未定の定数であり,モデルパラメータとなる.ま
た,4点相関関数は
![$\displaystyle \eta_{\rm g1234} = R_a \left[\xi_{\rm g12}\xi_{\rm g23}\xi_{\rm g...
...ht] + R_b \left[\xi_{\rm g12}\xi_{\rm g13}\xi_{\rm g14} + {\rm sim.}(4) \right]$](img4433.png) |
(O.2.30) |
となる.ここで,
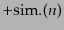 は直前の項を添字について対称に置換し
たものを足すことを表して略記したもので,直前の項を含めて
は直前の項を添字について対称に置換し
たものを足すことを表して略記したもので,直前の項を含めて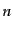 個の項があ
ることを示している.また,
個の項があ
ることを示している.また,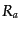 ,
, 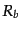 はモデルパラメータである.一般の
はモデルパラメータである.一般の
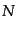 点相関関数
点相関関数
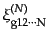 について形式的に表せば,
について形式的に表せば,
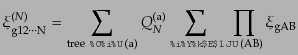 |
(O.2.31) |
と書ける.ここで,最初の和記号は,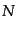 点を可能な全てのtreeグラフ,すな
わち,ループを作らないように
点を可能な全てのtreeグラフ,すな
わち,ループを作らないように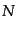 点を結ぶ方法について和を取ることを表す.
treeグラフの辺の数は必ず
点を結ぶ方法について和を取ることを表す.
treeグラフの辺の数は必ず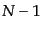 となる.また,次の和記号はそのtreeグラフ
の点のラベルを付け変えたものについて和を取ることを表す.次の積記号は,
点を結ぶ辺について対応する2点相関関数を掛け合わせることを表す.
となる.また,次の和記号はそのtreeグラフ
の点のラベルを付け変えたものについて和を取ることを表す.次の積記号は,
点を結ぶ辺について対応する2点相関関数を掛け合わせることを表す.
高次の相関関数は2点相関関数とは統計的に独立なものであるから,この相関
関数の階層モデルはもちろん一般的に成り立つものではない.観測的に銀河分
布については近似的に成り立つことが知られているが,より精密なレベルでは,
このモデルからの破れがあることも明らかになっている.
キュムラントと高次相関関数
銀河などの離散的な分布の相関関数の階層に対して,連続場に対しての相関関
数の階層が定義できる.2点相関関数はゆらぎの積の期待値で与えられたが,
多点の積の期待値が高次相関関数を与えることになる.だが,離散的分布の場
合と同様,より低次の相関関数に帰着できる情報を引き去ることにより,より
情報の重複のない統計量を取り扱う必要がある.
まず,一般論として,多自由度のランダム変数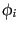 を考えることにする.
ここで,ランダム変数の積の期待値
を考えることにする.
ここで,ランダム変数の積の期待値
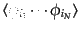 を
を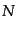 次のモーメントと呼ぶ.
このモーメントの既約成分として,
次のモーメントと呼ぶ.
このモーメントの既約成分として,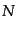 次のキュムラント
次のキュムラント
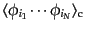 は次のように再帰的に
定義される:
は次のように再帰的に
定義される:
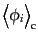 |
 |
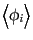 |
(O.2.32) |
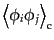 |
 |
 |
(O.2.33) |
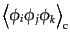 |
 |
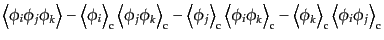 |
|
| |
|
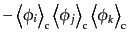 |
(O.2.34) |
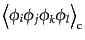 |
 |
![$\displaystyle \left\langle \phi_i \phi_j \phi_k \phi_l \right\rangle -
\left[
...
...rm c} \left\langle \phi_k \phi_l \right\rangle_{\rm c} + {\rm sim.}(3)
\right]$](img4450.png) |
|
| |
|
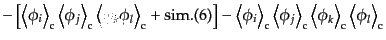 |
(O.2.35) |
つまり,キュムラントはモーメントから,あらゆる可能な重複しない部分集合
への組分けにより作られる,より低次のキュムラントの積を差し引いたもので
ある.逆に言えば,モーメントは重複しない部分集合への組分けによって作ら
れるキュムラントの積をあらゆる可能な場合について和を取ったもので与えら
れることになる:
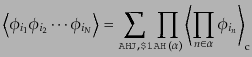 |
(O.2.36) |
この右辺は、クラスター展開に他ならない。ここで,左辺に現れて来る変数は
右辺に一度しか現れない.したがって,キュムラントは変数について線形性が
あることがすぐにわかる:
| |
|
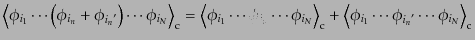 |
(O.2.37) |
| |
|
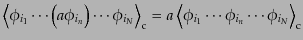 |
(O.2.38) |
ここで,ランダム変数として密度ゆらぎを取れば,こうして定義されるキュム
ラントが密度ゆらぎの高次相関関数を与える.点
 における密度ゆ
らぎの値を
における密度ゆ
らぎの値を
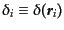 などと略記すれば,
などと略記すれば,
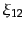 |
 |
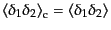 |
(O.2.39) |
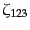 |
 |
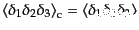 |
(O.2.40) |
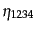 |
 |
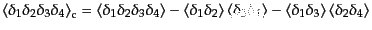 |
|
| |
|
 |
(O.2.41) |
のようになる.
離散的な天体分布の相関関数を,このキュムラントに関係づけることも可能で
ある.そのため,§15.1.2におけるように,空間を微小体積
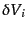 に分割して,その中の天体の数を
に分割して,その中の天体の数を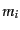 とすると,
とすると,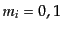 のみ
をとり、
のみ
をとり、
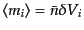 である.すると、
である.すると、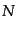 個の微小体積
個の微小体積
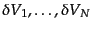 のすべてに天体が含まれる確
率は
のすべてに天体が含まれる確
率は
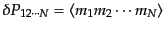 |
(O.2.42) |
で与えられる。ここで§15.2.1で見たように、左辺を
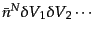 で割ったものをクラスター展開した
ときの最高次の項が高次相関関数である.したがって離散分布の
で割ったものをクラスター展開した
ときの最高次の項が高次相関関数である.したがって離散分布の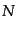 点相関関
数
点相関関
数
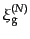 は右辺のキュムラントから
は右辺のキュムラントから
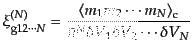 |
(O.2.43) |
と表されることがわかる。ここで,各微小体積中の個数に対するゆらぎに対応
する量
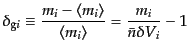 |
(O.2.44) |
を定義すれば、式(15.2.43)は
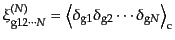 |
(O.2.45) |
と表すこともできる。これは、キュムラントの性質として変数の一つを定
数で置き換えたものは必ずゼロになることによる。
2点相関関数の場合と同様に,離散的な点分布の高次相関関数は,連続場の高
次相関関数に比べて,ショットノイズ項が付け加わる.式(15.1.14)を
導いたのと同様にすれば,その関係を求めることができる.ディラックのデル
タ関数を
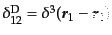 などのよ
うに略記すると,3点相関関数については
などのよ
うに略記すると,3点相関関数については
![$\displaystyle \zeta_{\rm g123} = \zeta_{\rm 123} + \frac{1}{\bar{n}} \left[ \de...
... \xi_{12} \right] + \frac{1}{\bar{n}^2} \delta^{\rm D}_{12} \delta^{\rm D}_{23}$](img4471.png) |
(O.2.46) |
となる.3点のうち2点のみが一致した場合と,3点とも一致した場合に対応
する項がショットノイズ項として現れている.4点相関関数については
| |
|
![$\displaystyle \eta_{\rm g1234} =
\zeta_{\rm 1234} +
\frac{1}{\bar{n}}
\left[
\delta^{\rm D}_{12} \zeta_{134} + {\rm sim.}(6)
\right]$](img4472.png) |
|
| |
|
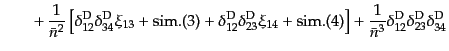 |
(O.2.47) |
となる.ショットノイズ項は,4点のうち,2点のみが一致する場合,2点ず
つ二組一致する場合,3点のみが一致する場合,4点ともに一致する場合に対
応している.より高次の相関関数のショットノイズ項の形ももこれらの例から
明らかであろう.





次へ: キュムラント展開定理
上へ: 天体分布の統計理論
前へ: 天体分布の相関関数とパワースペクトル
目次
索引
All rights reserved © T.Matsubara 2004-2010
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11
![]() は天体分布の分布を特徴づける一つの量であ
るが,この中に分布の統計的情報がすべて含まれているわけではない.銀河の
相関関数は2つの微小体積中に同時に銀河が存在する確率から定義することが
できた.その意味で,これは2点相関関数とも呼ばれる.これを拡張して,3つ
の微小体積
は天体分布の分布を特徴づける一つの量であ
るが,この中に分布の統計的情報がすべて含まれているわけではない.銀河の
相関関数は2つの微小体積中に同時に銀河が存在する確率から定義することが
できた.その意味で,これは2点相関関数とも呼ばれる.これを拡張して,3つ
の微小体積
![]() ,
,
![]() ,
,
![]() に同時に銀河が存在す
る確率
に同時に銀河が存在す
る確率
![]() から銀河の3点相関関数
から銀河の3点相関関数
![]() が次のように
定義される:
が次のように
定義される:
![]() は4つの
微小体積中に銀河が存在する確率により定義される:
は4つの
微小体積中に銀河が存在する確率により定義される:
![]() 点相関関数が
点相関関数が![]() 個の2点相関関数の積を組み合
わせたもので表されるようなモデルをを階層モデル (Hierarchical
model)と呼ぶ.この場合,対称性からその形はある程度決まるが,未定の定
数が含まれることになる.例えば,3点相関関数は
個の2点相関関数の積を組み合
わせたもので表されるようなモデルをを階層モデル (Hierarchical
model)と呼ぶ.この場合,対称性からその形はある程度決まるが,未定の定
数が含まれることになる.例えば,3点相関関数は
![]() を考えることにする.
ここで,ランダム変数の積の期待値
を考えることにする.
ここで,ランダム変数の積の期待値
![]() を
を![]() 次のモーメントと呼ぶ.
このモーメントの既約成分として,
次のモーメントと呼ぶ.
このモーメントの既約成分として,![]() 次のキュムラント
次のキュムラント
![]() は次のように再帰的に
定義される:
は次のように再帰的に
定義される:
![]() における密度ゆ
らぎの値を
における密度ゆ
らぎの値を
![]() などと略記すれば,
などと略記すれば,
![]() に分割して,その中の天体の数を
に分割して,その中の天体の数を![]() とすると,
とすると,![]() のみ
をとり、
のみ
をとり、
![]() である.すると、
である.すると、![]() 個の微小体積
個の微小体積
![]() のすべてに天体が含まれる確
率は
のすべてに天体が含まれる確
率は
![]() などのよ
うに略記すると,3点相関関数については
などのよ
うに略記すると,3点相関関数については
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11