




次へ: 宇宙背景放射ゆらぎ
上へ: 摂動宇宙における観測
前へ: ザックス・ヴォルフェ効果
目次
索引
Subsections
重力レンズ効果
上で見たように,質量なし粒子が膨張宇宙を進んでいくときのエネルギー変化
に対して,ザックスヴォルフェ効果は宇宙のゆらぎの影響を表している.一方,
この粒子に対するゆらぎの影響はエネルギーに対するもののみではなく,粒子
の運動経路も変化させる.この結果,この粒子によって観測される天体の位置
は,ゆらぎがない場合とは異なる位置に観測されることになる.これはちょう
ど重力ポテンシャルが粒子の経路を曲げることに相当し,宇宙のゆらぎがレン
ズの役割をする.この効果は重力レンズ効果(Gravitational lens
effect)
と呼ばれている.
摂動宇宙での重力レンズ効果を調べるため,摂動計量を用いた測地線方程式の
空間成分の式(13.1.17)から出発する.粒子の経路変化に対し,観測
される重力レンズ効果は天球面上に投影された成分である.そこで,3次元空間
の座標として観測者を中心とする球座標
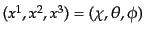 を
考えると便利である.その非摂動計量はRW計量(2.3.22)の空間部であ
り,
を
考えると便利である.その非摂動計量はRW計量(2.3.22)の空間部であ
り,
 |
(M.3.29) |
と書くことができる.ただしこの式および以下では
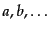 を角方
向
を角方
向
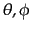 のいずれかを表す添字とし,さらに
のいずれかを表す添字とし,さらに
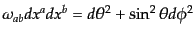 |
(M.3.30) |
は球面の計量である.この記法により3次元クリストッフェル記号
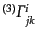 を動径方向
を動径方向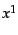 と角度方向
と角度方向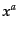 に分けて計算すると,
に分けて計算すると,
| |
|
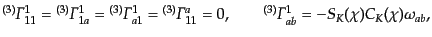 |
|
| |
|
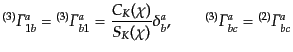 |
(M.3.31) |
となる.ここで,
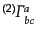 は計量
は計量
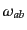 から導かれ
る球面の2次元クリストッフェル記号である.また,式(13.1.13)はい
ま,
から導かれ
る球面の2次元クリストッフェル記号である.また,式(13.1.13)はい
ま,
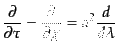 |
(M.3.32) |
となる.これらにより,式(13.1.17)の角成分を計算すれば,
![$\displaystyle a^2 \frac{d}{d\lambda} \left( a^2 \delta P^a \right) - 2 a^2 \fra...
...ht) - \frac{\partial}{\partial x^b} \left( A - B_1 - C_{11} \right) \right] = 0$](img4338.png) |
(M.3.33) |
となる.ここで,
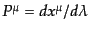 だから,
だから,
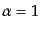 とおいた
式(13.1.8)により非摂動レベルの測地線上で,
とおいた
式(13.1.8)により非摂動レベルの測地線上で,
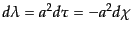 が成り立つ.摂動レベルでは測地線の摂動
が成り立つ.摂動レベルでは測地線の摂動
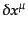 について
について
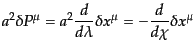 |
(M.3.34) |
が成り立つ.ここで、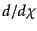 は測地線に沿った動系方向のラグランジュ微分
である.これらのことから式(13.3.33)は
は測地線に沿った動系方向のラグランジュ微分
である.これらのことから式(13.3.33)は
![$\displaystyle \frac{d^2}{d\chi^2}\delta x^a + 2 \frac{{C_K}(\chi)}{{S_K}(\chi)}...
...ht) + \frac{\partial}{\partial x^b} \left( A - B_1 - C_{11} \right) \right] = 0$](img4343.png) |
(M.3.35) |
と変形される.いま,角方向の測地線の摂動を表す新しい変数として,
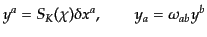 |
(M.3.36) |
を導入すれば,方程式が
![$\displaystyle \frac{d^2 y_a}{d\chi^2} + K y_a + \frac{1}{{S_K}(\chi)} \left[ \f...
...ht) + \frac{\partial}{\partial x^a} \left( A - B_1 - C_{11} \right) \right] = 0$](img4345.png) |
(M.3.37) |
という形になる.この方程式は左辺第3項を非斉次項とする2階線形微分方程式
であり、式(12.6.317)で構成したグリーン関数の方法によって一般解が
求められる.斉次方程式
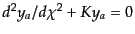 の独立な2解は
の独立な2解は
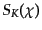 ,
,
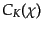 であるから,一般解は
であるから,一般解は
$](img4348.png) |
(M.3.38) |
となる.ここで積分の![$ [\cdots]$](img1440.png) の中は
の中は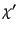 上での値である.
上での値である.
a





次へ: 宇宙背景放射ゆらぎ
上へ: 摂動宇宙における観測
前へ: ザックス・ヴォルフェ効果
目次
索引
All rights reserved © T.Matsubara 2004-2010
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11
![]() を
考えると便利である.その非摂動計量はRW計量(2.3.22)の空間部であ
り,
を
考えると便利である.その非摂動計量はRW計量(2.3.22)の空間部であ
り,
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11