




次へ: 摂動宇宙における観測
上へ: 摂動の線形成長
前へ: 諸成分ゆらぎの進化 I: 超ホライズンスケール
目次
索引
Subsections
諸成分ゆらぎの進化 II: 強結合近似とゆらぎの成長
宇宙の諸成分のうち,無衝突成分であるニュートリノとダークマターについて
は,重力ポテンシャル中を運動するだけであり,比較的単調な振る舞いをする.
一方,バリオンと光子はお互いに衝突するため,ゆらぎのスケー
ルに応じてホライズン内で音響振動を行う.
ここではその振る舞いを解析的に調べるため,方程式を強結合近似
(tight-coupling approximation) L3に基づいて取り扱うことを考
える.強結合近似とは,光子が電子に衝突
せずに進める距離が,考えている摂動モードの波長スケールよりも十分に小さ
いという場合の近似である.この場合には光子とバリオンは強く結合するため,
衝突項の係数
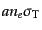 が十分に大きくなる.この係数の逆数
が十分に大きくなる.この係数の逆数
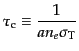 |
(L.6.279) |
は光子が散乱される平均的な共形時間間隔であるが、強結合近似ではこれが考
えているスケールに比べて小さい.すなわち量
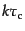 が十分小さい
場合を考える.
が十分小さい
場合を考える.
光子とバリオンの発展方程式(12.4.217)-(12.4.221),
(12.4.246), (12.4.247)を
 によって書き直
せば,
によって書き直
せば,
| |
|
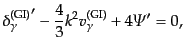 |
(L.6.280) |
| |
|
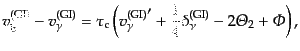 |
(L.6.281) |
| |
|
![$\displaystyle {\mit\Theta}_2 =
- \frac13 \tau_{\rm c}
\left[
4 {{\mit\Theta}...
...ta}_3 + {\mit\Theta}_{{\rm P} 1} + {\mit\Theta}_{{\rm P} 3}
\right)
\right]$](img4200.png) |
(L.6.282) |
| |
|
![$\displaystyle {\mit\Theta}_l =
-\tau_{\rm c}
\left\{
{{\mit\Theta}_l}' -
\...
...it\Theta}_{l-1} -
(l+1){\mit\Theta}_{l+1}\right]
\right\},
\quad (l \geq 3),$](img4201.png) |
(L.6.283) |
| |
|
![$\displaystyle {\mit\Theta}_{{\rm P} 0} =
- \frac13 \tau_{\rm c}
\left[
5 {{...
...a}_3 + 2{\mit\Theta}_{{\rm P} 1} + {\mit\Theta}_{{\rm P} 3}
\right)
\right]$](img4202.png) |
(L.6.284) |
| |
|
![$\displaystyle {\mit\Theta}_{{\rm P} 1}
= - \tau_{\rm c}
\left[
{{\mit\Theta...
...
\left({\mit\Theta}_{{\rm P} 0} - 2{\mit\Theta}_{{\rm P} 2}\right)
\right],$](img4203.png) |
(L.6.285) |
| |
|
![$\displaystyle {\mit\Theta}_{{\rm P} 2} =
- \frac13 \tau_{\rm c}
\left[
{{\m...
...a}_3 - {\mit\Theta}_{{\rm P} 1} + 4{\mit\Theta}_{{\rm P} 3}
\right)
\right]$](img4204.png) |
(L.6.286) |
| |
|
![$\displaystyle {\mit\Theta}_{{\rm P} l} =
- \tau_{\rm c}
\left\{
{{\mit\Thet...
... l-1} - (l+1){\mit\Theta}_{{\rm P} l+1}
\right]
\right\},
\quad (l \geq 3)$](img4205.png) |
(L.6.287) |
| |
|
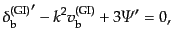 |
(L.6.288) |
| |
|
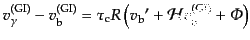 |
(L.6.289) |
となる.ここで
 を含む項はすべて右辺にくるように変形し,特
にその形を保ちつつ左辺にくる
を含む項はすべて右辺にくるように変形し,特
にその形を保ちつつ左辺にくる
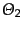 ,
,
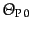 ,
,
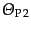 の線形結合をあらわに解いた形になるようにした.こ
の形により,
の線形結合をあらわに解いた形になるようにした.こ
の形により,
 が小さい場合に低次のオーダーから順番に解いて
いくことができる.ただし最後の式において,
が小さい場合に低次のオーダーから順番に解いて
いくことができる.ただし最後の式において,
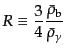 |
(L.6.290) |
である.この量は式(6.4.90)の3番目の等式(これはダークマターなど他
の成分があっても成立する)により,バリオン・光子の混合流体の音速
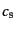 と次の関係にある:
と次の関係にある:
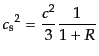 |
(L.6.291) |
まず,強結合近似の0次のオーダーの解を求めよう.式
(12.6.285)-(12.6.294)において
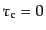 と置けば,
これらの方程式系は
と置けば,
これらの方程式系は
| |
|
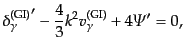 |
(L.6.292) |
| |
|
 |
(L.6.293) |
| |
|
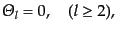 |
(L.6.294) |
| |
|
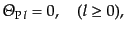 |
(L.6.295) |
| |
|
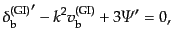 |
(L.6.296) |
となる.これら0次の式は完全な強結合の極限を表している.式
(12.6.298)は,バリオンと光子が完全に結合して速度が等しくなって
いることを表している.また,この極限では光子の偏光は存在しない.これは,
光子とバリオンの結合が強いため,バリオン静止系に対して光子の分布が等方
化してしまうことによる.偏光は非等方分布から生じるので,この場合生じる
ことができないのである.式(12.6.297), (12.6.298),
(12.6.301)から容易に
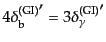 が得られる.これは式(12.5.264で見
たように,バリオン-エントロピー比
が得られる.これは式(12.5.264で見
たように,バリオン-エントロピー比
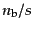 のゆらぎが時間変化しないことを意味し、
宇宙初期には空間的に一定値をとると考えられるので,解は
のゆらぎが時間変化しないことを意味し、
宇宙初期には空間的に一定値をとると考えられるので,解は
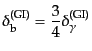 |
(L.6.297) |
となる.こうして,バリオンと光子は一体となって成長する.
次に強結合近似の1次の方程式を考える.上で得られた0次の解を式
(12.6.285)-(12.6.294)の右辺に代入することにより,
| |
|
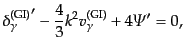 |
(L.6.298) |
| |
|
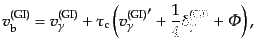 |
(L.6.299) |
| |
|
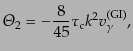 |
(L.6.300) |
| |
|
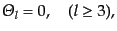 |
(L.6.301) |
| |
|
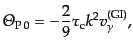 |
(L.6.302) |
| |
|
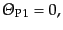 |
(L.6.303) |
| |
|
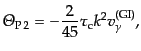 |
(L.6.304) |
| |
|
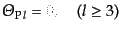 |
(L.6.305) |
| |
|
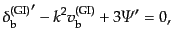 |
(L.6.306) |
| |
|
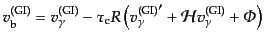 |
(L.6.307) |
を得る.式(12.6.305)を見ると,強結合近似の1次の効果として4重極
成分
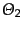 が発生していることがわかる.これは散乱と散乱の間に光子
が自由運動することで分布の双極子成分
が発生していることがわかる.これは散乱と散乱の間に光子
が自由運動することで分布の双極子成分
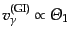 が4重極子成分を生み出すためである.そうして生み出された4重
極成分は散乱によりさらに偏極成分を生みだす.式(12.6.305),
(12.6.307), (12.6.309)から
が4重極子成分を生み出すためである.そうして生み出された4重
極成分は散乱によりさらに偏極成分を生みだす.式(12.6.305),
(12.6.307), (12.6.309)から
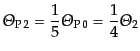 |
(L.6.308) |
という関係があるので,偏極は分布の4重極成分に比例し,
![$\displaystyle {\mit\Theta}_{\rm P} = \frac54 \left[1 - P_2(\mu)\right] {\mit\Theta}_2$](img4227.png) |
(L.6.309) |
で与えられる.
こうして,光子の双極子成分が4重極成分と偏極成分を決定づけていることが
わかる.ここでポテンシャルを外場とみなせば,双極子成分は式
(12.6.303) により単極子成分
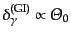 から求められる.そこで,単極子成分の発展方程式を求めると都合
がよいことがわかるだろう.他に単極子成分を含む方程式は式
(12.6.304)であるが,これはバリオンの速度場
から求められる.そこで,単極子成分の発展方程式を求めると都合
がよいことがわかるだろう.他に単極子成分を含む方程式は式
(12.6.304)であるが,これはバリオンの速度場
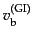 を含んでいるので,さらに式(12.6.312)を用いて
を含んでいるので,さらに式(12.6.312)を用いて
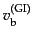 を消去すると,
を消去すると,
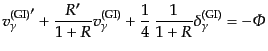 |
(L.6.310) |
が得られる.ただしここで,式(12.4.238)により示される式
 を用いた.この式と式(12.6.303)から
を用いた.この式と式(12.6.303)から
 を消去すれば,単極子成分に関する発展方程式
を消去すれば,単極子成分に関する発展方程式
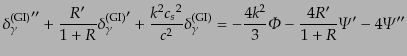 |
(L.6.311) |
を得る.
この方程式は左辺を強制項とし,まさつのある振動子を表す線形2階微分方程
式となっている.つまり,左辺で表される変動重力ポテンシャ
ルの影響を受けつつ,光子のエネルギー密度が自己重力と圧力により振動する
音響振動の様子を記述していて、その角振動数は
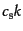 で与えられるこ
とが読み取れる.
で与えられるこ
とが読み取れる.
一般に,1変数の線形微分方程式では,強制項のない斉次方程式の解をすべて求
めることができれば,グリーン関数が構成でき,もとの方程式の一般解を求め
ることができる.一般に強制項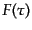 を持つ2階微分方程式について,そ
の斉次方程式の2つの独立解を
を持つ2階微分方程式について,そ
の斉次方程式の2つの独立解を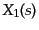 ,
, 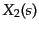 とすれば,一般解は斉次方
程式の一般解に非斉次方程式の特解を加えた形
とすれば,一般解は斉次方
程式の一般解に非斉次方程式の特解を加えた形
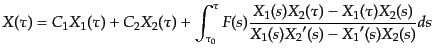 |
(L.6.312) |
で与えられる.ここで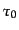 は初期値を与える点である.そこで,式
(12.6.316)の解を求めるにはその斉次方程式の一般解を求めればよい
ことになる.
は初期値を与える点である.そこで,式
(12.6.316)の解を求めるにはその斉次方程式の一般解を求めればよい
ことになる.
だが正確な一般解を求めることは難しいので,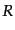 の時間変化よりも十分速く
振動する解を考えてWKB近似によって求めることにする.節
6.3.4と同様に計算することにより,斉次方程式の独立な2解と
して,
の時間変化よりも十分速く
振動する解を考えてWKB近似によって求めることにする.節
6.3.4と同様に計算することにより,斉次方程式の独立な2解と
して,
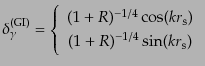 |
(L.6.313) |
が得られる.ただし,
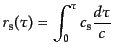 |
(L.6.314) |
は音響ホライズン (sound horizon)
,す
なわち音速が宇宙年齢の間に到達できる距離である.この量は式
(4.2.29)および式(12.6.296)の近似のもとでこれらの式,および
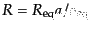 となることを使えば積分でき,
となることを使えば積分でき,
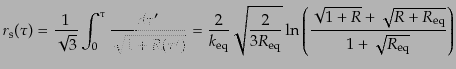 |
(L.6.315) |
となる.ただしここで,
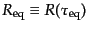 は等密度時の
は等密度時の
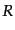 の値,
の値,
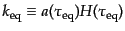 は等密
度時のホライズンスケールの波数である.WKB解(12.6.318)を式
(12.6.317)に用いれば式(12.6.316)の近似解が求まり,
は等密
度時のホライズンスケールの波数である.WKB解(12.6.318)を式
(12.6.317)に用いれば式(12.6.316)の近似解が求まり,
となり,この式は近似を用いずに数値計算をして得られる振動の様子を非常に
よく表すことが知られているL4.
ここで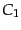 ,
, 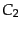 は積分定数であり,上に求めた超ホライズンスケールの振
る舞いから決まる初期条件から定まる.
このために,上の式を微分してみると,いま,WKB近似を用いているので,振動
部以外の因子として出てくる
は積分定数であり,上に求めた超ホライズンスケールの振
る舞いから決まる初期条件から定まる.
このために,上の式を微分してみると,いま,WKB近似を用いているので,振動
部以外の因子として出てくる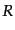 の微分は無視して,
の微分は無視して,
となる.したがって,式(12.5.279), (12.5.283)により,
断熱ゆらぎに対し,
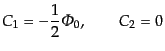 |
(L.6.316) |
また等曲率ゆらぎに対し,
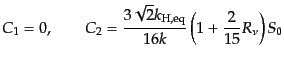 |
(L.6.317) |
と係数が求まる.
この近似解(12.6.321)から、斉次解の効かない領域では,断熱ゆらぎ
のとき
![$ \cos[kr_{\rm s}(\tau)]$](img4255.png) ,等曲率ゆらぎのとき
,等曲率ゆらぎのとき
![$ \sin[kr_{\rm
s}(\tau)]$](img4256.png) で表される振動をし,ゆらぎのタイプによって振動の位相が異な
ることがわかる. 断熱ゆらぎの場合には光子-バリオン系のゆらぎの波数が
で表される振動をし,ゆらぎのタイプによって振動の位相が異な
ることがわかる. 断熱ゆらぎの場合には光子-バリオン系のゆらぎの波数が
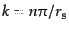 , (
, (
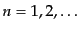 )を満たす位置にピークがあり,等
曲率ゆらぎの場合には
)を満たす位置にピークがあり,等
曲率ゆらぎの場合には
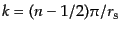 の位置にピークがある.こ
の違いは宇宙の晴れ上がりのときの背景放射のゆらぎに反映される.宇宙の初
期条件に対して観測可能な予言を与える極めて重要な事実である.また,物質
優勢期を考えると重力ポテンシャルはダークマターによってほとんど決定づけ
られるのでポテンシャルは振動しない.すると,式(12.6.303)におい
て,双極子成分
の位置にピークがある.こ
の違いは宇宙の晴れ上がりのときの背景放射のゆらぎに反映される.宇宙の初
期条件に対して観測可能な予言を与える極めて重要な事実である.また,物質
優勢期を考えると重力ポテンシャルはダークマターによってほとんど決定づけ
られるのでポテンシャルは振動しない.すると,式(12.6.303)におい
て,双極子成分
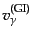 も波数の関数として振動していて,そ
の位相は
も波数の関数として振動していて,そ
の位相は
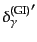 の振動の位相と一致する. これは単
極子成分
の振動の位相と一致する. これは単
極子成分
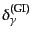 と位相が
と位相が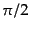 ずれている.さらに式
(12.6.305)より双極子成分の位相は4重極子成分と位相が一致し,また,
式(12.6.314)より,偏極成分とも位相が一致する.つまり,光子の密
度ゆらぎと偏極のゆらぎはスケールの関数として位相が
ずれている.さらに式
(12.6.305)より双極子成分の位相は4重極子成分と位相が一致し,また,
式(12.6.314)より,偏極成分とも位相が一致する.つまり,光子の密
度ゆらぎと偏極のゆらぎはスケールの関数として位相が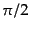 ずれることが
わかる.実際には非斉次解があるのでこれよりも多少複雑であるが,定性的
な結果はあまり変わらない.これはゆらぎの初期条件によらない重要な帰結で
あり,やはり宇宙の背景放射の観測によって検証可能なのである.
ずれることが
わかる.実際には非斉次解があるのでこれよりも多少複雑であるが,定性的
な結果はあまり変わらない.これはゆらぎの初期条件によらない重要な帰結で
あり,やはり宇宙の背景放射の観測によって検証可能なのである.
バリオンのゆらぎも光子のゆらぎと全く同様に振る舞う.実際,ここで考えて
いる強結合の1次近似では式(12.6.304), (12.6.312)の右辺に
おいて0次近似の解
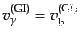 ,
,
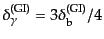 を代入してもよ
い.したがって,光子の場合の式(12.6.315)に対応して,
を代入してもよ
い.したがって,光子の場合の式(12.6.315)に対応して,
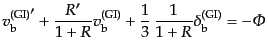 |
(L.6.318) |
が得られる.この式と式(12.6.311)により
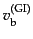 を
消去すれば,バリオンゆらぎの発展方程式
を
消去すれば,バリオンゆらぎの発展方程式
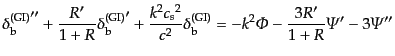 |
(L.6.319) |
が得られる.この式は光子に対する発展方程式(12.6.316)において
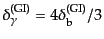 を代入したもの
となっている.したがって,初期条件が同じであれば,ゆらぎの振動の様子は
全く同じである.一般には,その差
を代入したもの
となっている.したがって,初期条件が同じであれば,ゆらぎの振動の様子は
全く同じである.一般には,その差
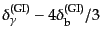 は上式の斉次方程式の解である.だが,式
(12.5.273)で見たように初期条件においても近似的に
は上式の斉次方程式の解である.だが,式
(12.5.273)で見たように初期条件においても近似的に
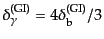 の関係があるか
ら、強結合の1次近似でもバリオンと光子はほぼ一体となって振る舞う.
の関係があるか
ら、強結合の1次近似でもバリオンと光子はほぼ一体となって振る舞う.
強結合近似が完全でないと高次の効果が重要になってくるが,それは光子の平
均自由行程のスケールであるから,このような高次の効果は比較的小スケール
において顕著である.光子とバリオンの結合が十分でないと,光子は高密度領
域から低密度領域へ洩れだし,小さなスケールのゆらぎをならすことになる.
これをゆらぎの拡散減衰 (diffusion damping),あるいはシルク減衰 (Silk
damping)ともい
う.この効果は観測的にも重要であるので,以下にその振る舞いを見積もって
みる.
放射優勢期のホライズン内のゆらぎは圧力により密度ゆらぎが成長できず,
式(12.2.48), (12.2.55)により重力ポテンシャルは
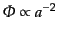 のように急速に減衰していくので,発展方程式において無視で
きるようになる.また,小スケールでは光子の時間的な振動スケールは宇宙膨
張の変化スケールよりも十分短いので,
のように急速に減衰していくので,発展方程式において無視で
きるようになる.また,小スケールでは光子の時間的な振動スケールは宇宙膨
張の変化スケールよりも十分短いので,
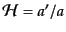 の表れる項を無視するこ
とができる.これらの近似において,式(12.6.303)から,
の表れる項を無視するこ
とができる.これらの近似において,式(12.6.303)から,
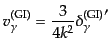 |
(L.6.320) |
である.つぎに
強結合近似の1次近
似の式(12.6.304)の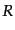 倍と式(12.6.312)を加えると
倍と式(12.6.312)を加えると
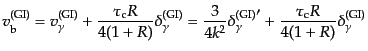 |
(L.6.321) |
を得る.さらに,式(12.6.305)から,
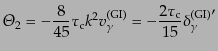 |
(L.6.322) |
となる.これら1次近似の式を
式(12.6.286)と式
(12.6.294)の右辺に代入したものは2次近似の式となり,その辺々を加
えると,
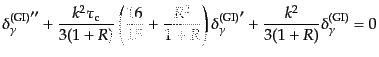 |
(L.6.323) |
を得る.ただし,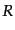 ,
,
 の時間変化は光子の振動スケールよりも
十分長いため,これらの微分は落とした.この式で
の時間変化は光子の振動スケールよりも
十分長いため,これらの微分は落とした.この式で
 の項を落と
せば,いま用いている近似において1次近似の方程式(12.6.316)と同じ
ものになる.右辺第2項が強結合近似の2次の効果となっている.この微分方程
式の係数はゆっくりと変化することからWKB解を求めれば,
の項を落と
せば,いま用いている近似において1次近似の方程式(12.6.316)と同じ
ものになる.右辺第2項が強結合近似の2次の効果となっている.この微分方程
式の係数はゆっくりと変化することからWKB解を求めれば,
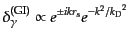 |
(L.6.324) |
を得る.ここで
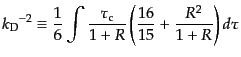 |
(L.6.325) |
であり,減衰スケール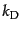 よりも小さなスケールで急激に光子のゆら
ぎが減衰していることがわかる.
よりも小さなスケールで急激に光子のゆら
ぎが減衰していることがわかる.
Footnotes
- ...
approximationL3
- P. J. E. Peebles and J. T. Yu, The
Astrophysical Journal 162, 815 (1970)
- ...
よく表すことが知られているL4
- W. Hu and N. Sugiyama, Phys. Rev.
D 51, 2599 (1995); Astrophys. J. 444, 489 (1995)





次へ: 摂動宇宙における観測
上へ: 摂動の線形成長
前へ: 諸成分ゆらぎの進化 I: 超ホライズンスケール
目次
索引
All rights reserved © T.Matsubara 2004-2010
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11
![]() が十分に大きくなる.この係数の逆数
が十分に大きくなる.この係数の逆数
![]() によって書き直
せば,
によって書き直
せば,
![]() と置けば,
これらの方程式系は
と置けば,
これらの方程式系は
![]() から求められる.そこで,単極子成分の発展方程式を求めると都合
がよいことがわかるだろう.他に単極子成分を含む方程式は式
(12.6.304)であるが,これはバリオンの速度場
から求められる.そこで,単極子成分の発展方程式を求めると都合
がよいことがわかるだろう.他に単極子成分を含む方程式は式
(12.6.304)であるが,これはバリオンの速度場
![]() を含んでいるので,さらに式(12.6.312)を用いて
を含んでいるので,さらに式(12.6.312)を用いて
![]() を消去すると,
を消去すると,
![]() を持つ2階微分方程式について,そ
の斉次方程式の2つの独立解を
を持つ2階微分方程式について,そ
の斉次方程式の2つの独立解を![]() ,
, ![]() とすれば,一般解は斉次方
程式の一般解に非斉次方程式の特解を加えた形
とすれば,一般解は斉次方
程式の一般解に非斉次方程式の特解を加えた形
![]() の時間変化よりも十分速く
振動する解を考えてWKB近似によって求めることにする.節
6.3.4と同様に計算することにより,斉次方程式の独立な2解と
して,
の時間変化よりも十分速く
振動する解を考えてWKB近似によって求めることにする.節
6.3.4と同様に計算することにより,斉次方程式の独立な2解と
して,
![]() ,等曲率ゆらぎのとき
,等曲率ゆらぎのとき
![]() で表される振動をし,ゆらぎのタイプによって振動の位相が異な
ることがわかる. 断熱ゆらぎの場合には光子-バリオン系のゆらぎの波数が
で表される振動をし,ゆらぎのタイプによって振動の位相が異な
ることがわかる. 断熱ゆらぎの場合には光子-バリオン系のゆらぎの波数が
![]() , (
, (
![]() )を満たす位置にピークがあり,等
曲率ゆらぎの場合には
)を満たす位置にピークがあり,等
曲率ゆらぎの場合には
![]() の位置にピークがある.こ
の違いは宇宙の晴れ上がりのときの背景放射のゆらぎに反映される.宇宙の初
期条件に対して観測可能な予言を与える極めて重要な事実である.また,物質
優勢期を考えると重力ポテンシャルはダークマターによってほとんど決定づけ
られるのでポテンシャルは振動しない.すると,式(12.6.303)におい
て,双極子成分
の位置にピークがある.こ
の違いは宇宙の晴れ上がりのときの背景放射のゆらぎに反映される.宇宙の初
期条件に対して観測可能な予言を与える極めて重要な事実である.また,物質
優勢期を考えると重力ポテンシャルはダークマターによってほとんど決定づけ
られるのでポテンシャルは振動しない.すると,式(12.6.303)におい
て,双極子成分
![]() も波数の関数として振動していて,そ
の位相は
も波数の関数として振動していて,そ
の位相は
![]() の振動の位相と一致する. これは単
極子成分
の振動の位相と一致する. これは単
極子成分
![]() と位相が
と位相が![]() ずれている.さらに式
(12.6.305)より双極子成分の位相は4重極子成分と位相が一致し,また,
式(12.6.314)より,偏極成分とも位相が一致する.つまり,光子の密
度ゆらぎと偏極のゆらぎはスケールの関数として位相が
ずれている.さらに式
(12.6.305)より双極子成分の位相は4重極子成分と位相が一致し,また,
式(12.6.314)より,偏極成分とも位相が一致する.つまり,光子の密
度ゆらぎと偏極のゆらぎはスケールの関数として位相が![]() ずれることが
わかる.実際には非斉次解があるのでこれよりも多少複雑であるが,定性的
な結果はあまり変わらない.これはゆらぎの初期条件によらない重要な帰結で
あり,やはり宇宙の背景放射の観測によって検証可能なのである.
ずれることが
わかる.実際には非斉次解があるのでこれよりも多少複雑であるが,定性的
な結果はあまり変わらない.これはゆらぎの初期条件によらない重要な帰結で
あり,やはり宇宙の背景放射の観測によって検証可能なのである.
![]() ,
,
![]() を代入してもよ
い.したがって,光子の場合の式(12.6.315)に対応して,
を代入してもよ
い.したがって,光子の場合の式(12.6.315)に対応して,
![]() のように急速に減衰していくので,発展方程式において無視で
きるようになる.また,小スケールでは光子の時間的な振動スケールは宇宙膨
張の変化スケールよりも十分短いので,
のように急速に減衰していくので,発展方程式において無視で
きるようになる.また,小スケールでは光子の時間的な振動スケールは宇宙膨
張の変化スケールよりも十分短いので,
![]() の表れる項を無視するこ
とができる.これらの近似において,式(12.6.303)から,
の表れる項を無視するこ
とができる.これらの近似において,式(12.6.303)から,
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11