




次へ: 宇宙の諸成分ゆらぎの発展方程式
上へ: 摂動の線形成長
前へ: 宇宙の優勢成分のゆらぎ
目次
索引
Subsections
2成分系のゆらぎの成長
2成分系のゆらぎの進化を調べる.ここでは簡単のため,成分間には相互作用
がなく,各成分のエントロピーゆらぎ ,非等方ストレス
,非等方ストレス
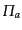 が
無視できるものとする.この場合,成分ごとのゆらぎを考えるかわりに,全ゆ
らぎとエントロピーのゆらぎを考えると便利である.いま,2成分
が
無視できるものとする.この場合,成分ごとのゆらぎを考えるかわりに,全ゆ
らぎとエントロピーのゆらぎを考えると便利である.いま,2成分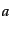 ,
,  の
みが存在する場合を考えると,任意のゲージにおける成分ごとの密度ゆらぎ
の
みが存在する場合を考えると,任意のゲージにおける成分ごとの密度ゆらぎ
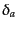 ,
, 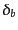 は全ゆらぎ
は全ゆらぎ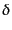 とエントロピー摂動
とエントロピー摂動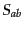 と
の間に,
と
の間に,
の関係がある.全ゆらぎ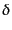 の進化はバーディーン変数に対して式
(10.4.170)により記述される.十分初期の宇宙を考え,アインシュタイ
ン・ドジッター宇宙で近似されるものとしよう.するといまの場合,
の進化はバーディーン変数に対して式
(10.4.170)により記述される.十分初期の宇宙を考え,アインシュタイ
ン・ドジッター宇宙で近似されるものとしよう.するといまの場合,
| |
|
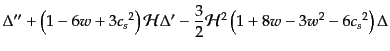 |
|
| |
|
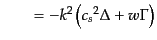 |
(L.3.65) |
という形になる.ここで,全体のエントロピーゆらぎは
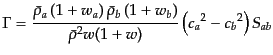 |
(L.3.66) |
で与えられる.エントロピー摂動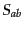 の進化は式(10.7.244)と式
(10.7.246)を組み合わせて記述される.いまの場合,それらの式は
の進化は式(10.7.244)と式
(10.7.246)を組み合わせて記述される.いまの場合,それらの式は
| |
|
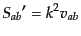 |
(L.3.67) |
| |
|
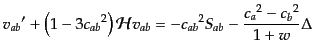 |
(L.3.68) |
となる.ここで,
 |
(L.3.69) |
である.したがって,エントロピー摂動の発展方程式は
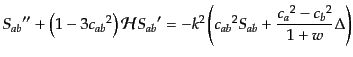 |
(L.3.70) |
となる.
これらの式から分かるように,一般に密度ゆらぎとエントロピーゆらぎの成長
は独立ではなく,両者は結合している.だが,その結合の項には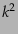 がかかっ
ているので,長波長極限
がかかっ
ているので,長波長極限
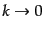 では独立に成長することがわかる.
系の時間変化のオーダーは長さにしてホライズンスケールであるから,このこ
とはすなわち,ホライズンよりも十分大きなスケールのゆらぎは密度ゆらぎと
エントロピーゆらぎが独立な成長をすることを意味している.さらにこの極限
では,式(12.3.67)により,エントロピー摂動
では独立に成長することがわかる.
系の時間変化のオーダーは長さにしてホライズンスケールであるから,このこ
とはすなわち,ホライズンよりも十分大きなスケールのゆらぎは密度ゆらぎと
エントロピーゆらぎが独立な成長をすることを意味している.さらにこの極限
では,式(12.3.67)により,エントロピー摂動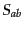 がほぼ一定に保
たれる.宇宙初期へ遡ればどのスケールもホライズンよりも十分大きくなると
考えられるので,初期条件としてエントロピーゆらぎと全密度ゆらぎを独立に
与えることができる.このことから初期ゆらぎは2種類に分類されて,エント
ロピーゆらぎがなく全密度ゆらぎのみの断熱ゆらぎ,逆に全密度ゆらぎ
がなくエントロピーゆらぎのみの等曲率ゆらぎに分けられる.これらの
名前の示す性質はゆらぎが超ホライズンスケールにとどまる間保たれ,独立な
モードと考えることができるので,一般解を両者の重ね合わせと考えてよい.
ホライズンスケールに入ってくれば両者の時間発展は混合し,そのような扱い
はできない.
がほぼ一定に保
たれる.宇宙初期へ遡ればどのスケールもホライズンよりも十分大きくなると
考えられるので,初期条件としてエントロピーゆらぎと全密度ゆらぎを独立に
与えることができる.このことから初期ゆらぎは2種類に分類されて,エント
ロピーゆらぎがなく全密度ゆらぎのみの断熱ゆらぎ,逆に全密度ゆらぎ
がなくエントロピーゆらぎのみの等曲率ゆらぎに分けられる.これらの
名前の示す性質はゆらぎが超ホライズンスケールにとどまる間保たれ,独立な
モードと考えることができるので,一般解を両者の重ね合わせと考えてよい.
ホライズンスケールに入ってくれば両者の時間発展は混合し,そのような扱い
はできない.
現実に近い具体的な系として,コールドダークマターと輻射の混在する場合を
調べてみよう.これにより一成分系の近似では分からなかった,等密度時前後
のホライズンスケールまたはそれ以下のスケールのゆらぎのふるまいについて
の知見が得られる.ここで,時間変数の代わりに等密度時を基準としたスケー
ル因子
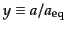 を用いると便利である.また,等密度時にお
けるダークマターと輻射の密度の和の一様成分を
を用いると便利である.また,等密度時にお
けるダークマターと輻射の密度の和の一様成分を
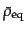 とす
る.ダークマターのエネルギー密度は
とす
る.ダークマターのエネルギー密度は
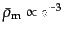 とスケールするので,ダークマターに関する物理量の一様成分は
とスケールするので,ダークマターに関する物理量の一様成分は
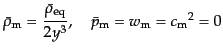 |
|
|
(L.3.71) |
また,輻射については
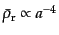 のスケールと
のスケールと
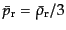 により,
により,
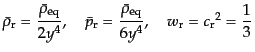 |
|
|
(L.3.72) |
となる.したがって,全体の物理量としては
| |
|
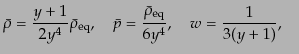 |
(L.3.73) |
| |
|
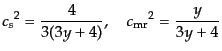 |
(L.3.74) |
となる.さらに,等密度時のハッブルパラメータを
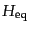 とすれば,等
密度時のホライズンスケールは
とすれば,等
密度時のホライズンスケールは
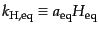 で与えられる.すると,式(3.3.41), (3.4.43)により
で与えられる.すると,式(3.3.41), (3.4.43)により
| |
|
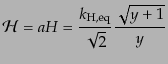 |
(L.3.75) |
| |
|
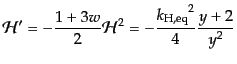 |
(L.3.76) |
となる.ここで,等密度時におけるフリードマン方程式(3.3.40)を使う
と,式(3.3.41)および
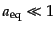 により,
により,
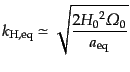 |
(L.3.77) |
と表すこともできる.
以下,エントロピー摂動を
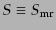 と省略して書く.
式(10.7.240)で与えられる共動ゲージにおける成分ごとのゆらぎの組
と省略して書く.
式(10.7.240)で与えられる共動ゲージにおける成分ごとのゆらぎの組
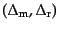 と,全密度ゆらぎとエントロピー摂動
の組
と,全密度ゆらぎとエントロピー摂動
の組
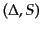 との間の関係を求めれば,
との間の関係を求めれば,
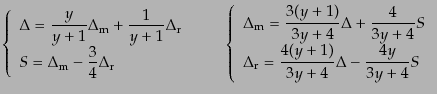 |
(L.3.78) |
となり,全エントロピーのゆらぎは
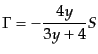 |
(L.3.79) |
で与えられる.ここで,エントロピー摂動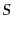 はエントロピー密度
はエントロピー密度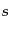 あたりの
ダークマターの数密度
あたりの
ダークマターの数密度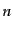 のゆらぎに等しいことを注意しておく.実際,エントロ
ピーはほとんどが放射によって担われていることと,
のゆらぎに等しいことを注意しておく.実際,エントロ
ピーはほとんどが放射によって担われていることと,
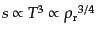 ,
,
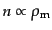 であることから,
であることから,
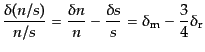 |
(L.3.80) |
となる.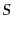 はゲージ不変なので,上式は
はゲージ不変なので,上式は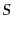 そのものである.ゆらぎの発展の
式を書き下すのに,微分演算子
そのものである.ゆらぎの発展の
式を書き下すのに,微分演算子
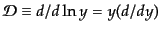 を用いる
と便利である.このとき,コンフォーマル時間に関する微分は
を用いる
と便利である.このとき,コンフォーマル時間に関する微分は
| |
|
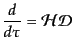 |
(L.3.81) |
| |
|
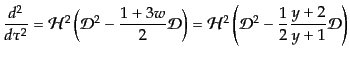 |
(L.3.82) |
となる.また,スケール を等密度時にちょうどホライズンサイズとなるス
ケール
を等密度時にちょうどホライズンサイズとなるス
ケール
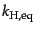 で規格化したスケール
で規格化したスケール
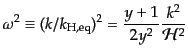 |
(L.3.83) |
を用いる.その結果,式(12.3.65), (12.3.70)は
となる.この式は多少複雑で,一般解は解析的に求まらないが,数値的に求め
ることは容易である.初期条件として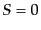 をとれば断熱ゆらぎ,
をとれば断熱ゆらぎ,
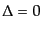 をとれば等曲率ゆらぎの発展を計算できるが,前に述べたように,これらの
発展はホライズンスケールに入ると独立ではない.したがって,ホライズンス
ケールをまたぐ時間発展において両者を別々に扱うことはできない.だが,初
期ゆらぎの性質は現在よくわかっていないダークマターの詳細に依存するので,
通常は簡単のため,どちらか一方のゆらぎを調べることが多い.
をとれば等曲率ゆらぎの発展を計算できるが,前に述べたように,これらの
発展はホライズンスケールに入ると独立ではない.したがって,ホライズンス
ケールをまたぐ時間発展において両者を別々に扱うことはできない.だが,初
期ゆらぎの性質は現在よくわかっていないダークマターの詳細に依存するので,
通常は簡単のため,どちらか一方のゆらぎを調べることが多い.
ここまでに簡単に調べられた極限的な場合でアインシュタイン・ドジッター宇
宙の場合の情報はすべてこの式に含まれている.この式の極限をとることによ
り,ここまでに見た単純な取り扱いのできた場合を含めてその振る舞いを系統
的に見てみよう.
まず,放射優勢期から物質優勢期を通じて,ホライズンの外にとどまっている
超ホライズンスケールのゆらぎの振る舞いを調べる.これは,
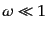 の極限をとることで調べることができる.上に述べた通り,密度ゆらぎとエン
トロピー摂動は独立な成長をする.超ホライズンスケールの密度ゆらぎの方程
式は,
の極限をとることで調べることができる.上に述べた通り,密度ゆらぎとエン
トロピー摂動は独立な成長をする.超ホライズンスケールの密度ゆらぎの方程
式は,
| |
|
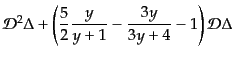 |
|
| |
|
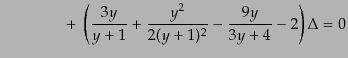 |
(L.3.86) |
となるが,この式は密度ゆらぎを
 とおくこ
とにより容易に積分できる形
とおくこ
とにより容易に積分できる形
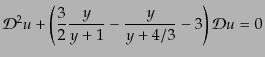 |
(L.3.87) |
となり,あとは直線的に解析解を求めることができる.その結果,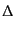 に
ついての独立な2解として,
に
ついての独立な2解として,
![$\displaystyle \frac{y^2}{y+1} \left[ 1 + \frac29 \frac{3+\sqrt{y+1}}{\left(1 + \sqrt{y+1}\right)^3} \right], \quad \frac{1}{y\sqrt{y+1}}$](img3868.png) |
(L.3.88) |
が求められる.ここで,第一の解は放射優勢期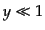 に
に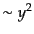 ,また,
物質優勢期
,また,
物質優勢期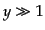 に
に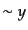 と振る舞い,いずれの時期でも成長
解になっている.これに対して第二の解は減衰解である.この成長解に対して,
ポテンシャル
と振る舞い,いずれの時期でも成長
解になっている.これに対して第二の解は減衰解である.この成長解に対して,
ポテンシャル
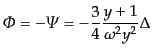 |
(L.3.89) |
は放射優勢期の極限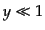 ,物質優勢期の極限
,物質優勢期の極限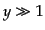 でいずれも一定値
を取ることがわかるので,ポテンシャルの初期値に対応する,放射優勢期の一
定値を
でいずれも一定値
を取ることがわかるので,ポテンシャルの初期値に対応する,放射優勢期の一
定値を
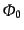 とおくことにより成長解の振幅が定まる.その結果と漸近形は,
とおくことにより成長解の振幅が定まる.その結果と漸近形は,
| |
|
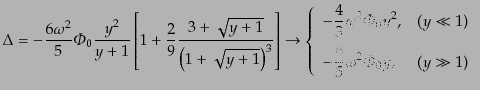 |
(L.3.90) |
| |
|
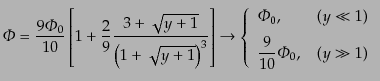 |
(L.3.91) |
という形となる.一成分系の接続解で導かれた,ポテンシャルが等密度時をは
さんで値が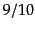 倍になるという結果は等密度時前後の時間発展を正確に扱っ
ても全く同じである.
倍になるという結果は等密度時前後の時間発展を正確に扱っ
ても全く同じである.
次に,エントロピー摂動の方程式は
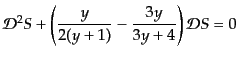 |
(L.3.92) |
となるが,これはすぐに積分できて,独立な2解は
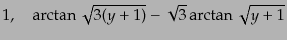 |
(L.3.93) |
である.第一の解は定数である.第二の解は放射優勢期の極限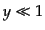 ,物
質優勢期の極限
,物
質優勢期の極限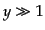 ともに一定値に近付いているが,その値は等密度時
をはさんで変化している.だが,エントロピー摂動が超ホライズンスケールで
変化するのは奇妙である.なぜなら,エントロピー摂動はエントロピーあたり
のダークマターの粒子数のゆらぎであり,この量は熱伝導がない限り一定値を
とるからである.超ホライズンスケールでの熱伝導はありえないので,エント
ロピー摂動の変化は因果律に反する.このことは次のようにも理解できる.式
(12.3.67)から,
ともに一定値に近付いているが,その値は等密度時
をはさんで変化している.だが,エントロピー摂動が超ホライズンスケールで
変化するのは奇妙である.なぜなら,エントロピー摂動はエントロピーあたり
のダークマターの粒子数のゆらぎであり,この量は熱伝導がない限り一定値を
とるからである.超ホライズンスケールでの熱伝導はありえないので,エント
ロピー摂動の変化は因果律に反する.このことは次のようにも理解できる.式
(12.3.67)から,
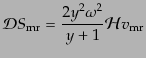 |
(L.3.94) |
となるので,超ホライズンスケールでのエントロピー摂動の時間変化は
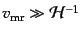 を要求するが,これは超ホライズンスケールの
運動をすることを意味するので,因果律に反することになる.したがって,因
果律を満たすエントロピー摂動は一定値をとる解のみである.この一定値を
を要求するが,これは超ホライズンスケールの
運動をすることを意味するので,因果律に反することになる.したがって,因
果律を満たすエントロピー摂動は一定値をとる解のみである.この一定値を
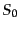 と書くことにする.
と書くことにする.
以上をまとめると,超ホライズンの一般のゆらぎはポテンシャル一定の密度ゆ
らぎと,エントロピー摂動一定のゆらぎを独立なモードとする重ね合わせで表
される.ポテンシャルは等密度時をはさんで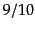 倍になるが,エントロピー
摂動は等密度時前後でも同じ一定値を取り続ける.
倍になるが,エントロピー
摂動は等密度時前後でも同じ一定値を取り続ける.
等曲率ゆらぎの場合は,はじめは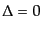 でも,式(12.3.84)の左辺
のエントロピー摂動の項をソース項として,少しずつ成長する.超ホライズン
スケールの極限を考えているので,
でも,式(12.3.84)の左辺
のエントロピー摂動の項をソース項として,少しずつ成長する.超ホライズン
スケールの極限を考えているので,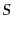 が一定であって
が一定であって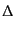 の成長と関係
なければ,強制項を持つ線形微分方程式となるので,斉次方程式の解からグリー
ン関数を作る方法によりこの式の解析解を求めることができる.その結果と漸
近形は
の成長と関係
なければ,強制項を持つ線形微分方程式となるので,斉次方程式の解からグリー
ン関数を作る方法によりこの式の解析解を求めることができる.その結果と漸
近形は
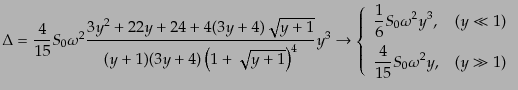 |
(L.3.95) |
となる.等曲率ゆらぎの超ホライズンスケールでは
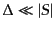 である.
このようにして,一定のエントロピーゆらぎから密度ゆらぎが生成されること
になる.
である.
このようにして,一定のエントロピーゆらぎから密度ゆらぎが生成されること
になる.
放射優勢期にホライズン内に入ってくるゆらぎを考える.
放射優勢期 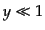 の極限をとると,式(12.3.84),
(12.3.85)は
の極限をとると,式(12.3.84),
(12.3.85)は
| |
|
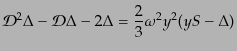 |
(L.3.96) |
| |
|
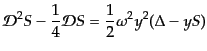 |
(L.3.97) |
y
となる.依然この式は2種類のゆらぎが結合していて解析的な取り扱いは繁雑
になるので,ここでは解析的に取り扱うためゆらぎがホライズン内に入るとき
の大スケールでの漸近形
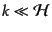 を考える.式(12.3.83)から,放
射優勢期では
を考える.式(12.3.83)から,放
射優勢期では
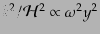 となるから,
となるから, を
小さな摂動として方程式を解けばよい.すると右辺は0次近似で無視でき,こ
の場合にはやはり密度ゆらぎとエントロピーゆらぎの成長は独立である.この
式は前節の計算で放射優勢の極限を取ったものとまったく同じであり,その0
次解は
を
小さな摂動として方程式を解けばよい.すると右辺は0次近似で無視でき,こ
の場合にはやはり密度ゆらぎとエントロピーゆらぎの成長は独立である.この
式は前節の計算で放射優勢の極限を取ったものとまったく同じであり,その0
次解は
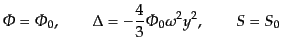 |
(L.3.98) |
である.
まず,断熱ゆらぎ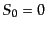 の場合を考える.この場合に上の0次解を式
(12.3.97)の右辺に代入すると,
の場合を考える.この場合に上の0次解を式
(12.3.97)の右辺に代入すると,
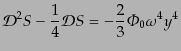 |
(L.3.99) |
となる.この方程式の成長解は容易に得られ,
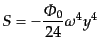 |
(L.3.100) |
となる.さて,密度ゆらぎが与えられれば,式
(10.5.182)により速度場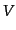 が得られる.いま放射優勢期で
が得られる.いま放射優勢期で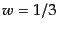 で
あるから,
で
あるから,
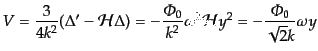 |
(L.3.101) |
となる.ただし,式(12.3.83)より放射優勢期では
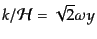 となることを用いた.
また式(10.6.201)により曲率ゆらぎ
となることを用いた.
また式(10.6.201)により曲率ゆらぎ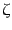 の表式が得られる.いま
の場合,
の表式が得られる.いま
の場合,
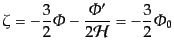 |
(L.3.102) |
と計算される.曲率ゆらぎが一定となることは節10.6での議論に一致
している.まとめると,放射優勢期にホライズンに入ってくるゆらぎの大スケー
ルにおける漸近形が
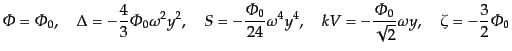 |
(L.3.103) |
という形となることが導かれた.
等曲率ゆらぎ
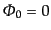 の場合も同様に求めることができる.すなわち,式
(12.3.96)の右辺に等曲率ゆらぎの0次解
の場合も同様に求めることができる.すなわち,式
(12.3.96)の右辺に等曲率ゆらぎの0次解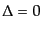 ,
, 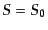 を代
入して同様に解けばよい.その結果,
を代
入して同様に解けばよい.その結果,
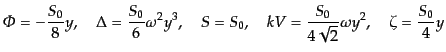 |
(L.3.104) |
が得られる.密度ゆらぎの式は当然,式(12.3.95)に一致している.ま
た,この場合には密度ゆらぎがエントロピーゆらぎに比べて小さいた
めに節10.6の密度ゆらぎの大きさに関する仮定が成立せず,曲率ゆら
ぎは保存していない.
次に,物質優勢期にホライズンに入ってくるゆらぎのスケールを考える.この
スケールのゆらぎは放射優勢期の成長の後,物質優勢期の成長を経験し,その
後ホライズンに入ってくる.ここでもホライズンに入ってくるゆらぎを大スケー
ルの漸近形(
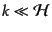 )として考えてみる.初期条件は放射優勢のときに
与えられるので,その初期条件により,物質優勢時のゆらぎを表す必要がある.
これはすでに超ホライズンスケールのゆらぎの成長のところで導かれてあるの
で,それを用いればよい.だがここでは曲率ゆらぎの成長を積分することによっ
て考えてみる.
)として考えてみる.初期条件は放射優勢のときに
与えられるので,その初期条件により,物質優勢時のゆらぎを表す必要がある.
これはすでに超ホライズンスケールのゆらぎの成長のところで導かれてあるの
で,それを用いればよい.だがここでは曲率ゆらぎの成長を積分することによっ
て考えてみる.
曲率ゆらぎの成長を表す式(10.6.200)はいま,非等方ストレス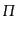 ,
曲率
,
曲率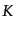 が無視できるので,式(10.4.172)を使えば
が無視できるので,式(10.4.172)を使えば
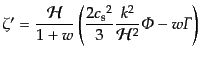 |
(L.3.105) |
となる.ところが,右辺括弧内の第一項は大スケールで消えるので,いまの近
似では無視でき,式(12.3.73), (12.3.79)を使えば
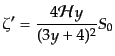 |
(L.3.106) |
となる.したがって断熱ゆらぎ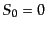 の場合には放射優勢期,物質優勢期を
通じて曲率ゆらぎは一定にとどまる.したがって,式(12.3.103)の値
の場合には放射優勢期,物質優勢期を
通じて曲率ゆらぎは一定にとどまる.したがって,式(12.3.103)の値
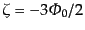 を物質優勢期まで保ち続ける.物質優勢期のとき,曲率
ゆらぎとポテンシャルの関係式(10.6.201)は
を物質優勢期まで保ち続ける.物質優勢期のとき,曲率
ゆらぎとポテンシャルの関係式(10.6.201)は
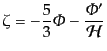 |
(L.3.107) |
となるので,これを
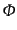 の微分方程式として
の微分方程式として
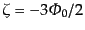 のときに積分すると,減衰項を無視 して
のときに積分すると,減衰項を無視 して
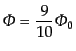 |
(L.3.108) |
となり,式(12.3.91)の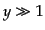 の場合を再現する.
の場合を再現する.
等曲率ゆらぎの場合には曲率ゆらぎは放射優勢期に成長するが,物質優勢期に
はやはり一定にとどまることがわかる.等曲率ゆらぎの場合に上式
(12.3.106)を積分すれば,初期条件で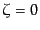 だから,
だから,
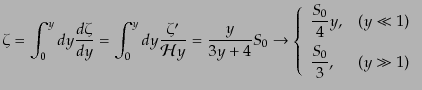 |
(L.3.109) |
となる.当然,放射優勢期の極限は式(12.3.104)に一致している.物質
優勢期の式をまた式(12.3.107)に入れた微分方程式を積分することによ
り,減衰項を無視して,
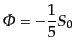 |
(L.3.110) |
を得る.
以上により,物質優勢期にホライズン内に入ってくるゆらぎは,大スケールの
極限で重力ポテンシャルとエントロピーが一定である.初期条件との間の遷移
行列として表せば,次のように表現できる:
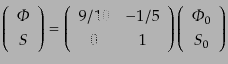 |
(L.3.111) |
あるいは重力ポテンシャルのかわりに曲率ゆらぎを使って表現すれば,
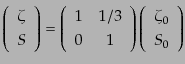 |
(L.3.112) |
となる.この遷移行列はホライズンの中に入る前のスケールのゆらぎの漸近形
であり,ホライズンに入るともっと複雑な形となるが,それを求めるには数値
積分を行う必要がある.





次へ: 宇宙の諸成分ゆらぎの発展方程式
上へ: 摂動の線形成長
前へ: 宇宙の優勢成分のゆらぎ
目次
索引
All rights reserved © T.Matsubara 2004-2010
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11
![]() ,非等方ストレス
,非等方ストレス
![]() が
無視できるものとする.この場合,成分ごとのゆらぎを考えるかわりに,全ゆ
らぎとエントロピーのゆらぎを考えると便利である.いま,2成分
が
無視できるものとする.この場合,成分ごとのゆらぎを考えるかわりに,全ゆ
らぎとエントロピーのゆらぎを考えると便利である.いま,2成分![]() ,
, ![]() の
みが存在する場合を考えると,任意のゲージにおける成分ごとの密度ゆらぎ
の
みが存在する場合を考えると,任意のゲージにおける成分ごとの密度ゆらぎ
![]() ,
, ![]() は全ゆらぎ
は全ゆらぎ![]() とエントロピー摂動
とエントロピー摂動![]() と
の間に,
と
の間に,
![]() がかかっ
ているので,長波長極限
がかかっ
ているので,長波長極限
![]() では独立に成長することがわかる.
系の時間変化のオーダーは長さにしてホライズンスケールであるから,このこ
とはすなわち,ホライズンよりも十分大きなスケールのゆらぎは密度ゆらぎと
エントロピーゆらぎが独立な成長をすることを意味している.さらにこの極限
では,式(12.3.67)により,エントロピー摂動
では独立に成長することがわかる.
系の時間変化のオーダーは長さにしてホライズンスケールであるから,このこ
とはすなわち,ホライズンよりも十分大きなスケールのゆらぎは密度ゆらぎと
エントロピーゆらぎが独立な成長をすることを意味している.さらにこの極限
では,式(12.3.67)により,エントロピー摂動![]() がほぼ一定に保
たれる.宇宙初期へ遡ればどのスケールもホライズンよりも十分大きくなると
考えられるので,初期条件としてエントロピーゆらぎと全密度ゆらぎを独立に
与えることができる.このことから初期ゆらぎは2種類に分類されて,エント
ロピーゆらぎがなく全密度ゆらぎのみの断熱ゆらぎ,逆に全密度ゆらぎ
がなくエントロピーゆらぎのみの等曲率ゆらぎに分けられる.これらの
名前の示す性質はゆらぎが超ホライズンスケールにとどまる間保たれ,独立な
モードと考えることができるので,一般解を両者の重ね合わせと考えてよい.
ホライズンスケールに入ってくれば両者の時間発展は混合し,そのような扱い
はできない.
がほぼ一定に保
たれる.宇宙初期へ遡ればどのスケールもホライズンよりも十分大きくなると
考えられるので,初期条件としてエントロピーゆらぎと全密度ゆらぎを独立に
与えることができる.このことから初期ゆらぎは2種類に分類されて,エント
ロピーゆらぎがなく全密度ゆらぎのみの断熱ゆらぎ,逆に全密度ゆらぎ
がなくエントロピーゆらぎのみの等曲率ゆらぎに分けられる.これらの
名前の示す性質はゆらぎが超ホライズンスケールにとどまる間保たれ,独立な
モードと考えることができるので,一般解を両者の重ね合わせと考えてよい.
ホライズンスケールに入ってくれば両者の時間発展は混合し,そのような扱い
はできない.
![]() を用いると便利である.また,等密度時にお
けるダークマターと輻射の密度の和の一様成分を
を用いると便利である.また,等密度時にお
けるダークマターと輻射の密度の和の一様成分を
![]() とす
る.ダークマターのエネルギー密度は
とす
る.ダークマターのエネルギー密度は
![]() とスケールするので,ダークマターに関する物理量の一様成分は
とスケールするので,ダークマターに関する物理量の一様成分は
![]() の極限をとることで調べることができる.上に述べた通り,密度ゆらぎとエン
トロピー摂動は独立な成長をする.超ホライズンスケールの密度ゆらぎの方程
式は,
の極限をとることで調べることができる.上に述べた通り,密度ゆらぎとエン
トロピー摂動は独立な成長をする.超ホライズンスケールの密度ゆらぎの方程
式は,
![]() 倍になるが,エントロピー
摂動は等密度時前後でも同じ一定値を取り続ける.
倍になるが,エントロピー
摂動は等密度時前後でも同じ一定値を取り続ける.
![]() でも,式(12.3.84)の左辺
のエントロピー摂動の項をソース項として,少しずつ成長する.超ホライズン
スケールの極限を考えているので,
でも,式(12.3.84)の左辺
のエントロピー摂動の項をソース項として,少しずつ成長する.超ホライズン
スケールの極限を考えているので,![]() が一定であって
が一定であって![]() の成長と関係
なければ,強制項を持つ線形微分方程式となるので,斉次方程式の解からグリー
ン関数を作る方法によりこの式の解析解を求めることができる.その結果と漸
近形は
の成長と関係
なければ,強制項を持つ線形微分方程式となるので,斉次方程式の解からグリー
ン関数を作る方法によりこの式の解析解を求めることができる.その結果と漸
近形は
![]() の極限をとると,式(12.3.84),
(12.3.85)は
の極限をとると,式(12.3.84),
(12.3.85)は
![]() の場合を考える.この場合に上の0次解を式
(12.3.97)の右辺に代入すると,
の場合を考える.この場合に上の0次解を式
(12.3.97)の右辺に代入すると,
![]() の場合も同様に求めることができる.すなわち,式
(12.3.96)の右辺に等曲率ゆらぎの0次解
の場合も同様に求めることができる.すなわち,式
(12.3.96)の右辺に等曲率ゆらぎの0次解![]() ,
, ![]() を代
入して同様に解けばよい.その結果,
を代
入して同様に解けばよい.その結果,
![]() )として考えてみる.初期条件は放射優勢のときに
与えられるので,その初期条件により,物質優勢時のゆらぎを表す必要がある.
これはすでに超ホライズンスケールのゆらぎの成長のところで導かれてあるの
で,それを用いればよい.だがここでは曲率ゆらぎの成長を積分することによっ
て考えてみる.
)として考えてみる.初期条件は放射優勢のときに
与えられるので,その初期条件により,物質優勢時のゆらぎを表す必要がある.
これはすでに超ホライズンスケールのゆらぎの成長のところで導かれてあるの
で,それを用いればよい.だがここでは曲率ゆらぎの成長を積分することによっ
て考えてみる.
![]() ,
曲率
,
曲率![]() が無視できるので,式(10.4.172)を使えば
が無視できるので,式(10.4.172)を使えば
![]() だから,
だから,
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11