




次へ: 摂動の線形成長
上へ: インフレーション理論におけるゆらぎの生成
前へ: スカラーゆらぎの生成
目次
索引
ここまで,インフレーション理論によるスカラーゆらぎの生成を詳しく見てき
た.これに対して,ベクトルゆらぎについてはスカラー場であるインフラトン
場には含まれず,何らかの理由で生成されたとしてもこのモードは成長しない
で減衰してしまうため,あまり興味はない.一方,テンソルゆらぎは重力波の
モードである.重力波は現在のところ観測されてはいないが,将来観測可能な
影響を及ぼす可能性があり,興味が持たれる.インフレーションにより生成さ
れる重力波はスカラーゆらぎの場合と同様に計算できる.本来,このプロセス
を正しく扱うには重力場の量子論が必須であるが,現在のところそのような理
論は完成していない.だが,重力場が弱く線形近似の範囲に限るならばスカラー
場の場合と同様に(少なくとも形式的には)生成される量子ゆらぎを計算するこ
とができる.その計算の正統性は明らかではないにせよ,少なくとも観測可能
性を予言するという点においては意味のあることであろう.
前章で導入されたテンソルゆらぎのモード
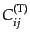 はトレースなし
かつ発散なしの成分であったから,4つの拘束条件
はトレースなし
かつ発散なしの成分であったから,4つの拘束条件
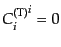 ,
,
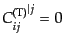 を満たし,3次元2階対称テンソルの6つの
成分のうち、自由度は都合2つである.この2つの自由度は偏極の自由度であ
り,通常
を満たし,3次元2階対称テンソルの6つの
成分のうち、自由度は都合2つである.この2つの自由度は偏極の自由度であ
り,通常
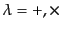 と書いて区別する.他の成分である,スカラー
成分,ベクトル成分は完全に独立な自由度であるからいまは考えなくてよい.
また,インフラトン場がそうであるように,非等方ストレスが無視できる場合
にはエネルギー運動量テンソルにテンソル成分は含まれていないので,重力波
モードは物質とは独立に取り扱える(運動方程式(10.4.130)も参照).さら
にテンソル摂動はそのままでゲージ不変であったから,ゲージ自由度に煩わさ
れる心配もなく,偏極の2自由度はそのまま物理的自由度である。この偏極の
2自由度について直線的に量子化することができる.
と書いて区別する.他の成分である,スカラー
成分,ベクトル成分は完全に独立な自由度であるからいまは考えなくてよい.
また,インフラトン場がそうであるように,非等方ストレスが無視できる場合
にはエネルギー運動量テンソルにテンソル成分は含まれていないので,重力波
モードは物質とは独立に取り扱える(運動方程式(10.4.130)も参照).さら
にテンソル摂動はそのままでゲージ不変であったから,ゲージ自由度に煩わさ
れる心配もなく,偏極の2自由度はそのまま物理的自由度である。この偏極の
2自由度について直線的に量子化することができる.
式(B.2.79)のアインシュタイン・ヒルベルト作用
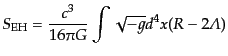 |
(K.3.110) |
から出発する.この作用にテンソル型摂動の計量
![$\displaystyle ds^2 = a^2(\tau) \left[ -d\tau^2 + \left(\gamma_{ij} + C^{\rm (T)}_{ij}\right) dx^i dx^j \right]$](img3640.png) |
(K.3.111) |
を代入し,摂動の2次の項を取り出し,テンソル型摂動の拘束条件を用いて消
える項は消し、さらに表面項を落とせば,結果的に
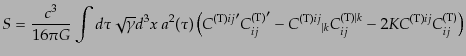 |
(K.3.112) |
となる.この作用を変分して得られる運動方程式
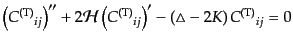 |
(K.3.113) |
は,当然ながら前章で導いたテンソル型摂動の運動方程式(10.4.130)で非
等方ストレスのない場合のものに一致する.これは一般の一様等方宇宙におけ
る重力波の伝播を記述するが,ここからは簡単のため,初期宇宙などで非摂動
空間計量が平坦な場合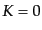 ,
,
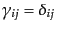 を考える.ここで,
次のようにスケールした変数
を考える.ここで,
次のようにスケールした変数
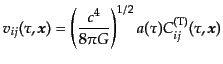 |
(K.3.114) |
を導入すると上の作用は
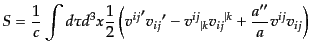 |
(K.3.115) |
となる.ただし,ここでも表面項を落とした.ここから導かれる運動方程式は
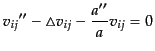 |
(K.3.116) |
となり,これはスカラー場の運動方程式(11.2.39)で
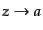 とおいたものに等しく,偏極成分が2つあることを別にすれば全く同様に量
子化して量子ゆらぎを求めることができるのである.
とおいたものに等しく,偏極成分が2つあることを別にすれば全く同様に量
子化して量子ゆらぎを求めることができるのである.
偏極の2つの自由度の基底として偏極テンソル
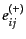 ,
,
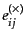 を導入すれば,スケールされたテンソル摂動の平面波展
開は
を導入すれば,スケールされたテンソル摂動の平面波展
開は
![$\displaystyle v_{ij} = \int \frac{d^3k}{(2\pi)^3 2k^0} \sum_{\lambda=+,\times} ...
...i{\mbox{\scriptsize\boldmath$k$}}\cdot{\mbox{\scriptsize\boldmath$x$}}} \right]$](img3650.png) |
(K.3.117) |
となる.ここで偏極テンソル
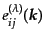 は対称テンソル
であり,また拘束条件から,次の性質を満すようなものである:
は対称テンソル
であり,また拘束条件から,次の性質を満すようなものである:
| |
|
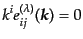 |
(K.3.118) |
| |
|
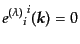 |
(K.3.119) |
さらに,直交規格化条件
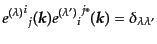 |
(K.3.120) |
を課す.例として,波数ベクトル
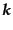 を
を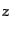 軸とするような座標系での具
体的表現を書けば,
軸とするような座標系での具
体的表現を書けば,
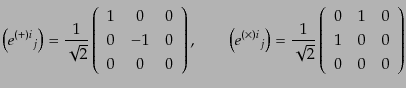 |
(K.3.121) |
となる.
こうして各偏極モードは完全に独立に考えてよくなり,生成消滅演算子の交換
関係は
![\begin{displaymath}\begin{array}{l} \left[ a_\lambda({\mbox{\boldmath$k$}}), a_{...
...ambda'}^\dagger({\mbox{\boldmath$k$}}') \right] = 0 \end{array}\end{displaymath}](img3656.png) |
(K.3.122) |
となる.ここからスカラーゆらぎの場合の式(11.2.59)に対応して,
生成されるパワースペクトルは
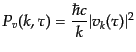 |
(K.3.123) |
となる.ここで,スカラーゆらぎの場合に比して,2つの偏極成分があるため
の因子2が考慮されている.
ここで,モード関数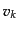 の満たす方程式は
の満たす方程式は
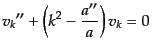 |
(K.3.124) |
であり,規格化条件は
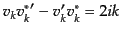 |
(K.3.125) |
である.この方程式をスローロール近似で解く.スローロールの関係式
(11.2.76)より,
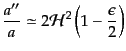 |
(K.3.126) |
であるがこれを
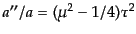 とおけば,式
(11.2.88)を用いて
とおけば,式
(11.2.88)を用いて
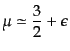 |
(K.3.127) |
となる.あとの計算はスカラー場の場合と全く同じで,解の長波長極限,つま
り超ハッブルスケール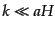 (
(
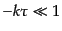 )における漸近形は
)における漸近形は
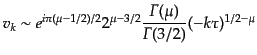 |
(K.3.128) |
となるので,式(11.3.113), (11.3.122)により
 の
振幅について,2つの偏極からの寄与を加えたパワースペクトル
の
振幅について,2つの偏極からの寄与を加えたパワースペクトル
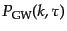 は
は
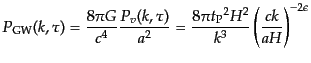 |
(K.3.129) |
あるいは無次元化されたスペクトルで表せば
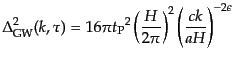 |
(K.3.130) |
となり,やはりほぼスケール不変なパワースペクトルが得られる.スケール不
変性からのずれを表すスペクトル指数は
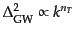 で定義され(スカラーゆらぎの場合のスペクトル指数の定義
と異なっていることに注意する),それはスローロールパラメータ
で定義され(スカラーゆらぎの場合のスペクトル指数の定義
と異なっていることに注意する),それはスローロールパラメータ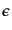 の
みで与えられ,
の
みで与えられ,
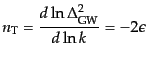 |
(K.3.131) |
である.
ここで,インフレーションによって生成されるテンソルゆらぎの振幅と式
(11.2.103)で与えられるスカラーゆらぎの振幅の比をとってみると,
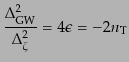 |
(K.3.132) |
となって,テンソルゆらぎのスペクトル指数と結びついている.これはいま考
えている,1種類のスカラー場のスローロールによってインフレーションが起
こるとするモデルでは必ず満たさなければならない関係で,単一場インフレー
ションにおける無矛盾性の関係 (The consistency relation)と呼ばれ
ている.





次へ: 摂動の線形成長
上へ: インフレーション理論におけるゆらぎの生成
前へ: スカラーゆらぎの生成
目次
索引
All rights reserved © T.Matsubara 2004-2010
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11
![]() はトレースなし
かつ発散なしの成分であったから,4つの拘束条件
はトレースなし
かつ発散なしの成分であったから,4つの拘束条件
![]() ,
,
![]() を満たし,3次元2階対称テンソルの6つの
成分のうち、自由度は都合2つである.この2つの自由度は偏極の自由度であ
り,通常
を満たし,3次元2階対称テンソルの6つの
成分のうち、自由度は都合2つである.この2つの自由度は偏極の自由度であ
り,通常
![]() と書いて区別する.他の成分である,スカラー
成分,ベクトル成分は完全に独立な自由度であるからいまは考えなくてよい.
また,インフラトン場がそうであるように,非等方ストレスが無視できる場合
にはエネルギー運動量テンソルにテンソル成分は含まれていないので,重力波
モードは物質とは独立に取り扱える(運動方程式(10.4.130)も参照).さら
にテンソル摂動はそのままでゲージ不変であったから,ゲージ自由度に煩わさ
れる心配もなく,偏極の2自由度はそのまま物理的自由度である。この偏極の
2自由度について直線的に量子化することができる.
と書いて区別する.他の成分である,スカラー
成分,ベクトル成分は完全に独立な自由度であるからいまは考えなくてよい.
また,インフラトン場がそうであるように,非等方ストレスが無視できる場合
にはエネルギー運動量テンソルにテンソル成分は含まれていないので,重力波
モードは物質とは独立に取り扱える(運動方程式(10.4.130)も参照).さら
にテンソル摂動はそのままでゲージ不変であったから,ゲージ自由度に煩わさ
れる心配もなく,偏極の2自由度はそのまま物理的自由度である。この偏極の
2自由度について直線的に量子化することができる.
![]() ,
,
![]() を導入すれば,スケールされたテンソル摂動の平面波展
開は
を導入すれば,スケールされたテンソル摂動の平面波展
開は
![]() の満たす方程式は
の満たす方程式は
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11