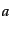 に対し,ボルツマン方程式(9.2.36)は,
に対し,ボルツマン方程式(9.2.36)は,
成分間にエネルギー・運動量の輸送がある場合,これまでのアインシュタイン
方程式だけでは不十分で,ボルツマン方程式を用いる必要がある.そこで,こ
の節ではボルツマン方程式の線形摂動に対する基本的な式を導く.粒子種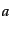 に対し,ボルツマン方程式(9.2.36)は,
に対し,ボルツマン方程式(9.2.36)は,
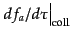 は単位共形時間あ
たりの衝突項である.4元運動量ベクトル
は単位共形時間あ
たりの衝突項である.4元運動量ベクトル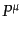 は質量殻上
は質量殻上
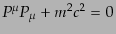 にある.この条件は摂動の1次で
にある.この条件は摂動の1次で
 の成分はしたがって3つのみが独立である.独
立変数として何をとるかは任意であるが,時間一定面(
の成分はしたがって3つのみが独立である.独
立変数として何をとるかは任意であるが,時間一定面(
 )に垂直な
方向に時間軸を持つような(すなわちシフトベクトルがゼロであるような)座標
系における3次元運動量を用いると以下の計算が簡略化して便利である.その
ような座標系としては座標条件として
)に垂直な
方向に時間軸を持つような(すなわちシフトベクトルがゼロであるような)座標
系における3次元運動量を用いると以下の計算が簡略化して便利である.その
ような座標系としては座標条件として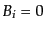 を持つようなもの,例えばコ
ンフォーマル・ニュートンゲージ(10.5.178)や,同期ゲージ
(10.5.179)があり,ボルツマン方程式の計算はこれらのゲージで行われ
ることも多い.だが,それでは特殊なゲージに依存した結果しか得られないの
で,ここでは時空座標自体のゲージ固定はせずに,運動量の独立変数を選ぶと
きのみ一時的に座標系を選ぶことにする.そこで,各時空座標点において,簡
単な局所座標
を持つようなもの,例えばコ
ンフォーマル・ニュートンゲージ(10.5.178)や,同期ゲージ
(10.5.179)があり,ボルツマン方程式の計算はこれらのゲージで行われ
ることも多い.だが,それでは特殊なゲージに依存した結果しか得られないの
で,ここでは時空座標自体のゲージ固定はせずに,運動量の独立変数を選ぶと
きのみ一時的に座標系を選ぶことにする.そこで,各時空座標点において,簡
単な局所座標 を張って,その座標系での運動量ベクトルの成分の値を
独立変数とする.非摂動一様等方計量と同じ形の計量を持つ局所座標を取るこ
とにすれば,そのテトラード
を張って,その座標系での運動量ベクトルの成分の値を
独立変数とする.非摂動一様等方計量と同じ形の計量を持つ局所座標を取るこ
とにすれば,そのテトラード
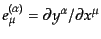 は次の規格化をみたす:
は次の規格化をみたす:
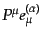 をスケー
ルした次の量
をスケー
ルした次の量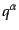 を定義する:
を定義する:
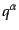 の独立成分は3つであるので,以下
の独立成分は3つであるので,以下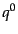 は従属変数と考え
る.また,分布関数
は従属変数と考え
る.また,分布関数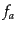 は非摂動部は運動量の絶対値にしか依らないので,
このベクトル
は非摂動部は運動量の絶対値にしか依らないので,
このベクトル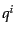 をさらに動径成分
をさらに動径成分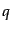 と方向ベクトル
と方向ベクトル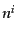 に分解すると都
合がよい:
に分解すると都
合がよい:
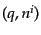 を運動量の独立変数にとる.上式を逆に解けば,
を運動量の独立変数にとる.上式を逆に解けば,
これらの運動量空間の新変数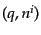 を用いてボルツマン方程式
(10.8.251を表し直すことを考える.この変数変換の係数は時空座標に依
存しているので、偏微分の変換は次のようになる:
を用いてボルツマン方程式
(10.8.251を表し直すことを考える.この変数変換の係数は時空座標に依
存しているので、偏微分の変換は次のようになる:
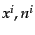 に依らないので,
に依らないので,
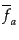 は非摂動部,
は非摂動部,
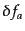 は摂動部である.
これらのことに注意して線形の項まで残して計算すると,新変数による線形ボ
ルツマン方程式は
は摂動部である.
これらのことに注意して線形の項まで残して計算すると,新変数による線形ボ
ルツマン方程式は
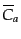 ,
,
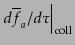 はそれぞれの衝
突項の非摂動部分である.また線形摂動部は
はそれぞれの衝
突項の非摂動部分である.また線形摂動部は
![$ \delta C_a[f_a]$](img3422.png) は衝突項の線形摂動部,
は衝突項の線形摂動部,
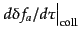 は共形時間あたりの衝突項
の線形摂動部である.
は共形時間あたりの衝突項
の線形摂動部である.
巨視的変数は分布関数の積分で表される.エネルギー・運動量テンソルを考え ると,式(9.1.14)により,
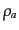 , 圧力
, 圧力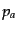 ,速度
,速度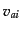 ,
および非等方ストレス
,
および非等方ストレス
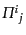 は式(10.4.119)-(10.4.123)か
ら
は式(10.4.119)-(10.4.123)か
ら
最後に分布関数のゲージ変換を調べておく.まず運動量は
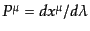 で定義されている.ここで,粒子の運動量はベクトル場では
なく場のゲージ変換とは異なることに注意する.するとゲージ変換
で定義されている.ここで,粒子の運動量はベクトル場では
なく場のゲージ変換とは異なることに注意する.するとゲージ変換
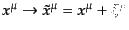 に対して
に対して
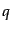 の定義に現れる変数のゲージ変換は
の定義に現れる変数のゲージ変換は
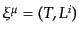 という記法を
用いている.これらの式から,式(10.8.258)の変換を計算すると,
という記法を
用いている.これらの式から,式(10.8.258)の変換を計算すると,
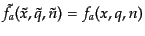 である.ここ
で,方向依存性は非摂動部を持たないので,
である.ここ
で,方向依存性は非摂動部を持たないので,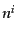 のゲージ変換は線形項には
効かないことに注意して,ゲージ変換を計算すると,
のゲージ変換は線形項には
効かないことに注意して,ゲージ変換を計算すると,
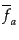 の時間
微分を消しながら注意深く計算すれば,次のゲージ不変な方程式を得る:
の時間
微分を消しながら注意深く計算すれば,次のゲージ不変な方程式を得る:
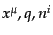 の関数として分配関数と同様にスカラーとして変換
するから,このゲージ不変量の定義は分布関数における式(10.8.290)と
類似のものになっている.
の関数として分配関数と同様にスカラーとして変換
するから,このゲージ不変量の定義は分布関数における式(10.8.290)と
類似のものになっている.
また,ゲージ不変な巨視的変数をゲージ不変分布関数で表すこともできる.式
(10.8.280)-(10.8.283)は,式(10.8.290)を積分すること
によって,
ベクトル型摂動についてのボルツマン方程式は式(10.8.268)のベク
トル型成分を取ることにより、式(10.4.86)のベクトル型ゲージ不変ポテ
ンシャル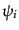 を用いて,
を用いて,
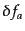 のゲージ変換(10.8.289)はベクトル型の変
換をしないので、
のゲージ変換(10.8.289)はベクトル型の変
換をしないので、
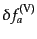 はそのままゲージ不変量である.
また,第2,3項はそれぞれの衝突項のベクトル型成分であり、左辺がゲージ不
変なので,衝突項もゲージ不変となる.
はそのままゲージ不変量である.
また,第2,3項はそれぞれの衝突項のベクトル型成分であり、左辺がゲージ不
変なので,衝突項もゲージ不変となる.
最後にテンソル型摂動の方程式は
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11