




次へ: トムソン散乱における偏光の取り扱い
上へ: 相対論的運動学
前へ: ボルツマン方程式
目次
索引
Subsections
我々が宇宙の観測により得られる情報はほとんど電磁波によるものである.こ
の理由により,光子と物質の相互作用は重要なプロセスであるが,なかでも光
子と電子の相互作用は非常に重要なものである.クライン・仁科の公式
(8.7.481)から分かるように,光子と自由荷電粒子の散乱において,
散乱確率は粒子の質量の2乗に反比例する.したがって,原子がイオン化して
いる状態では,光子は原子核よりも自由電子との散乱を最も強く受けることに
なる.そこでここでは光子と電子の相互作用系をとくに考えてみる.簡単のた
め,分布関数は光子の偏極自由度,電子のスピン自由度によらず,また,電子
は非相対論的になっているものとして,衝突過程はトムソン散乱であるとする.
電子-光子散乱は時間反転不変な相互作用である.ここで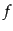 ,
, 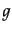 をそれぞれ
光子と電子の分布関数とし,それぞれ偏極とスピンの自由度にかかわらずに同
じ分布をするものと仮定する.このとき,光子に対する衝突項の形は
をそれぞれ
光子と電子の分布関数とし,それぞれ偏極とスピンの自由度にかかわらずに同
じ分布をするものと仮定する.このとき,光子に対する衝突項の形は
となる.ここで分配関数のあらわな時間依存性はは省略して書いてある.電子
の密度は希薄で古典統計が成り立つものとし,
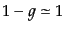 とした.また
とした.また
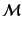 はトムソン散乱の不変散乱振幅である.その形はコンプトン散乱
の式(8.7.479)で古典極限をとれば得られる.ここで,電子のスピン、
光子の偏極にかかわらず同じ分布関数の形となっているので,積分されている
粒子のスピン自由度と偏極自由度については和をとり,注目する粒子について
は平均をとる.すると式(8.7.484)も用いることにより,
はトムソン散乱の不変散乱振幅である.その形はコンプトン散乱
の式(8.7.479)で古典極限をとれば得られる.ここで,電子のスピン、
光子の偏極にかかわらず同じ分布関数の形となっているので,積分されている
粒子のスピン自由度と偏極自由度については和をとり,注目する粒子について
は平均をとる.すると式(8.7.484)も用いることにより,
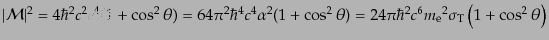 |
(I.3.81) |
となる.ここで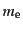 は電子の質量、また
は電子の質量、また
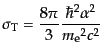 |
(I.3.82) |
はトムソン全断面積である.上の散乱振幅は入射粒子の静止系で導かれたもの
であったが,トムソン散乱において光子の散乱角は座標系によらなくなるので,
どの座標系においても同じ形になる.電子は非相対論的であるから,各運動量
4元ベクトルは
| |
|
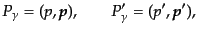 |
(I.3.83) |
| |
|
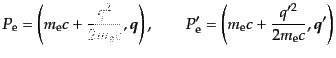 |
(I.3.84) |
とおける.ただしここで,
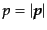 ,
,
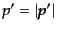 ,
,
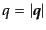 ,
,
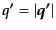 は3次元運動量の絶対値である.また,等方
的な分布を考えれば,分布関数は運動量の絶対値のみの関数
は3次元運動量の絶対値である.また,等方
的な分布を考えれば,分布関数は運動量の絶対値のみの関数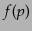 ,
, 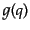 で
ある.
で
ある.
上の非相対論的近似において最低次のみを残すことにより衝突項は
| |
|
![$\displaystyle C[f(p)] =
\frac{3}{8\pi} \frac{\sigma_{\rm T}}{(2\pi\hbar)^3}
...
...p'}\right)^2\right]
\delta\left(p - p' + \frac{q^2 - q'^2}{2m_{\rm e}c}\right)$](img2690.png) |
|
| |
|
![$\displaystyle \qquad\qquad\qquad\quad \times
\delta^3({\mbox{\boldmath$p$}} - ...
...
f(p') g(q') \left[1 + f(p)\right] - f(p) g(q) \left[1 + f(p')\right]
\Bigr\}$](img2691.png) |
(I.3.85) |
と書き表される.トムソン散乱では光子のエネルギーは電子の静止エネルギー
よりも十分小さい,すなわち
 である.また電子は非相対論的であり,
電子の運動エネルギーと光子のエネルギーが同じオーダー,
である.また電子は非相対論的であり,
電子の運動エネルギーと光子のエネルギーが同じオーダー,
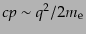 となる.したがって,
となる.したがって,
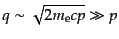 |
(I.3.86) |
となり,光子の典型的な運動量は電子の典型的な運動量に比べて十分小さい.
すると衝突の前後での光子の運動量の変化
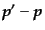 が電子の典型
運動量に比べて十分小さく,したがって電子の運動量変化
が電子の典型
運動量に比べて十分小さく,したがって電子の運動量変化
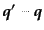 もまた
もまた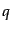 ,
, 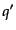 に比べて小さいことになる.そこで,上の衝突項の
積分を,
に比べて小さいことになる.そこで,上の衝突項の
積分を,
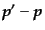 で展開して評価することを考える.そこで,デ
ルタ関数を2次まで展開することによりI3,
で展開して評価することを考える.そこで,デ
ルタ関数を2次まで展開することによりI3,
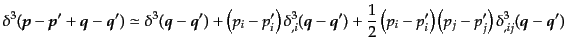 |
(I.3.87) |
を用いる.ここで,第一項は式(9.3.85)に入れると最初のデルタ関数
と合わせて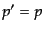 ,
, 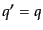 を導き,最後の因子が消えることになるので,
結局積分には寄与しない.また,第二項以下を評価するのに,光子の運動量の
角度積分に注目する.光子の分布関数は運動量の方向によらないものと仮定し
ているので,
を導き,最後の因子が消えることになるので,
結局積分には寄与しない.また,第二項以下を評価するのに,光子の運動量の
角度積分に注目する.光子の分布関数は運動量の方向によらないものと仮定し
ているので,
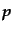 の角度平均をとっても衝突項の形は同じである.した
がって,積分の中では
の角度平均をとっても衝突項の形は同じである.した
がって,積分の中では
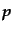 ,
,
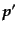 の角度依存項はその項の角度平
均に置き換えることができる.光子の角度依存因子は上の展開式の他にトムソ
ン散乱から出て来る因子がある.いずれにしても多項式の形で現れるので,そ
の角度積分は容易である.そのためには次の積分を用いればよい:
の角度依存項はその項の角度平
均に置き換えることができる.光子の角度依存因子は上の展開式の他にトムソ
ン散乱から出て来る因子がある.いずれにしても多項式の形で現れるので,そ
の角度積分は容易である.そのためには次の積分を用いればよい:
| |
|
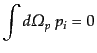 |
(I.3.88) |
| |
|
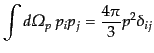 |
(I.3.89) |
| |
|
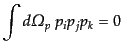 |
(I.3.90) |
| |
|
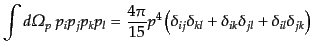 |
(I.3.91) |
その結果,式(9.3.87)の第二項は必ず奇数個の運動量角度積分となり消え
る.また第三項を含む角度積分を上式により計算すると,
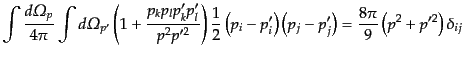 |
(I.3.92) |
となる.こうして,式(9.3.85)の角度積分が実行でき,
| |
|
![$\displaystyle C[f(p)] =
\frac{1}{3}\frac{\sigma_{\rm T}}{(2\pi\hbar)^3}
\int...
...'^3 + p^2 p'\right)
\delta\left(p - p' + \frac{q^2 - q'^2}{2m_{\rm e}c}\right)$](img2708.png) |
|
| |
|
![$\displaystyle \qquad\qquad\qquad \times
\left[
\frac{\partial}{\partial {\mbo...
...
f(p') g(q') \left[1 + f(p)\right] - f(p) g(q) \left[1 + f(p')\right]
\Bigr\}$](img2709.png) |
(I.3.93) |
となる.この表式をまず変数
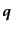 について部分積分を行う.任
意の関数
について部分積分を行う.任
意の関数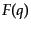 について,
について,
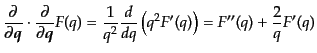 |
(I.3.94) |
となることを用いて微分を実行し,その後
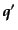 について積分すると
について積分すると
となる.さらに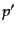 積分を部分積分を用いて実行すると,
積分を部分積分を用いて実行すると,
となる.ここで,積分の中の最後の項は動径方向の表面積分となり消える.他
の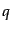 積分の一部は電子の数密度
積分の一部は電子の数密度
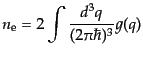 |
(I.3.97) |
により表される.ここで,前の因子 はスピン自由度である.さらにこの積
分の部分積分から,
はスピン自由度である.さらにこの積
分の部分積分から,
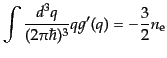 |
(I.3.98) |
が得られる.また非平衡状態の電子の温度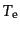 として自然な定義は
として自然な定義は
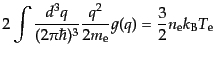 |
(I.3.99) |
である.ただし,電子の系全体としては重心は運動していないと仮定する.こ
れらの積分を用いて式(9.3.96)を変形すると簡潔な形
![$\displaystyle C[f(p)] = \frac{n_{\rm e} \sigma_{\rm T}}{m_{\rm e}c} \frac{1}{p}...
...k_{\rm B} T_{\rm e}}{c} \frac{\partial f}{\partial p} + f(1+f) \right] \right\}$](img2724.png) |
(I.3.100) |
となる.したがって,一様等方宇宙のボルツマン方程式(9.2.76)は
![$\displaystyle \frac{\partial f}{\partial t} - H p \frac{\partial f}{\partial p}...
...k_{\rm B} T_{\rm e}}{c} \frac{\partial f}{\partial p} + f(1+f) \right] \right\}$](img2725.png) |
(I.3.101) |
となる.これは電子の分布関数が与えられたとき,光子の分布関数を決める方
程式であり、重要な式である.
式(9.3.101)を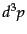 積分すると、衝突項は部分積分により表面項となっ
て消える.左辺も部分積分することにより,
積分すると、衝突項は部分積分により表面項となっ
て消える.左辺も部分積分することにより,
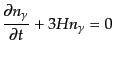 |
(I.3.102) |
となる.ここで,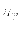 は光子の数密度で,
は光子の数密度で,
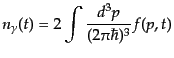 |
(I.3.103) |
である.式(9.3.102)は共動体積あたりの光子の数
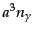 が
一定となることを表すが,これは当然ながら電子-光子散乱における最低次の
近似では光子の数が保たれているからである.
が
一定となることを表すが,これは当然ながら電子-光子散乱における最低次の
近似では光子の数が保たれているからである.
宇宙膨張の効果が無視できるスケールを考えるときには式(9.3.101)左
辺第2項は必要ない.その場合,次のような変数のスケール
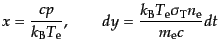 |
(I.3.104) |
をすることにより,より簡単な式
![$\displaystyle \frac{\partial f}{\partial y} = \frac{1}{x^2} \frac{\partial}{\partial x} \left[ x^4 \left(\frac{\partial f}{\partial x} + f(1+f)\right) \right]$](img2732.png) |
(I.3.105) |
となる.この式をカンパニエーツ方程式 (Kompaneets equation)という
I4.ここ
で導入した変数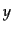 は
は
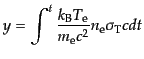 |
(I.3.106) |
と書くことができ,区間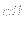 の光学的厚さに電子の運動エネルギーと静止エ
ネルギーの比をかけて積分したものである.この比は平均的な光子のドップラー
偏移を表す[式(8.7.482)参照].したがってこのパラメータ
の光学的厚さに電子の運動エネルギーと静止エ
ネルギーの比をかけて積分したものである.この比は平均的な光子のドップラー
偏移を表す[式(8.7.482)参照].したがってこのパラメータ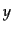 は考え
ている積分区間における光子の平均的な振動数の変化を表すものと解釈できる.
この量
は考え
ている積分区間における光子の平均的な振動数の変化を表すものと解釈できる.
この量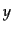 をコンプトン化パラメータ (Comptonization parameter)と呼
ぶ.
をコンプトン化パラメータ (Comptonization parameter)と呼
ぶ.
上で得た一様等方宇宙の光子のボルツマン方程式(9.3.101)の応用とし
て,晴れ上がり以前の宇宙の熱進化における光子と物質の熱平衡化のプロセス
を調べてみる.まず,光子のエネルギー密度は
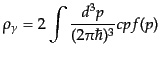 |
(I.3.107) |
で与えられる.光子の温度がどのように定義するのが自然であるのかを考える
ため,平衡状態の分布関数
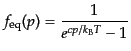 |
(I.3.108) |
における温度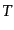 を考える.すると,
を考える.すると,
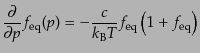 |
(I.3.109) |
となるから,部分積分により,
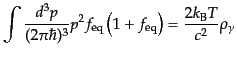 |
(I.3.110) |
となる.そこで,非平衡状態においてもこの最後の式を光子の温度の定義と考
えることにするのが自然である:
![$\displaystyle T_\gamma \equiv \frac{c^2}{2 k_{\rm B} \rho_\gamma} \int \frac{d^3p}{(2\pi\hbar)^3} p^2 f(p) \left[1+f(p)\right]$](img2739.png) |
(I.3.111) |
この準備の下,式(9.3.101)に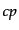 をかけてから
をかけてから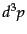 積分をすると,
適切な部分積分の後,
積分をすると,
適切な部分積分の後,
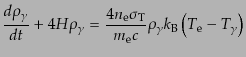 |
(I.3.112) |
を得る.この式はWeymannにより初めて導かれたI5.この式は電子の温度が光子の温度よりも高ければ
電子が光子を暖めることを表している.あるいは逆に電子の温度が低ければ光
子は電子によって冷やされることになる.
いま,簡単な近似として,宇宙の物質は完全にイオン化した水素原子のみから
成っているものとする.すると,物質は同数の電子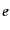 と陽子
と陽子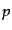 のプラズマ状
態にあって,お互いに強く相互作用して同じ温度
のプラズマ状
態にあって,お互いに強く相互作用して同じ温度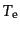 をもつと考える
ことができる.すると,エネルギー密度はそれぞれ
をもつと考える
ことができる.すると,エネルギー密度はそれぞれ
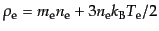 ,
,
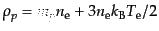 で与えられ,圧力は
で与えられ,圧力は
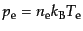 ,
,
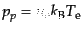 で与えられる.したがってプラズマのエネルギー密度と圧力は
で与えられる.したがってプラズマのエネルギー密度と圧力は
である.ただし,電子の質量は陽子の質量に比べて無視できるので落とした.
さて,膨張宇宙ではマクロな観点からエントロピー保存則(3.1.14)すな
わち,
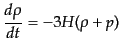 |
(I.3.115) |
が成り立つので,これに
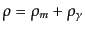 ,
,
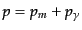 と式(9.3.114)および
と式(9.3.114)および
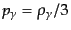 を代入して,
を代入して,
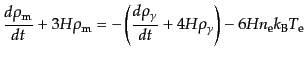 |
(I.3.116) |
を得る.一方,トムソン散乱の前後で電子の数は変化しないので,共動体積あ
たりの電子数は保存し,
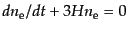 が成り立つ.し
たがって,式(9.3.113)より
が成り立つ.し
たがって,式(9.3.113)より
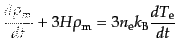 |
(I.3.117) |
が成り立つ.したがって式(9.3.112), (9.3.116),
(9.3.117)により,電子の温度変化の式
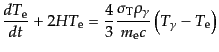 |
(I.3.118) |
が導かれる.この式はもし光子の温度の方が大きければその分電子が暖められ,
逆に光子の温度が小さければ電子が冷まされることを表している.いずれにし
ても電子の温度は光子の温度に近づこうとする.左辺の第2項は,自由な非相
対論的粒子の運動エネルギーが宇宙膨張によって
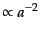 で減少する
ことから来る,まさつ項となっている.
で減少する
ことから来る,まさつ項となっている.
光子とバリオンの数は式(4.6.62)から8桁以上の違いで光子の方が多
い:
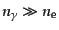 .すると光子の光学的厚さ
.すると光子の光学的厚さ
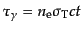 と電子の光学的厚さ
と電子の光学的厚さ
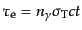 では,
では,
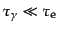 とな
るので,決まった時間内にある電子がまわりの光子に散乱される回数は,ある
光子がまわりの電子に散乱される回数よりも圧倒的に多くなる.したがって,
光子のエネルギー分布関数を変化させることは,電子の分布関数を変化させる
よりもずっと難しくなる.すると,光子は平衡状態からさほどずれていないと
期待できるので,式(4.1.8) による
とな
るので,決まった時間内にある電子がまわりの光子に散乱される回数は,ある
光子がまわりの電子に散乱される回数よりも圧倒的に多くなる.したがって,
光子のエネルギー分布関数を変化させることは,電子の分布関数を変化させる
よりもずっと難しくなる.すると,光子は平衡状態からさほどずれていないと
期待できるので,式(4.1.8) による
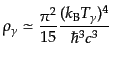 |
(I.3.119) |
と近似できる.宇宙膨張が無視できるような時間スケールにおいて, 光子の
温度はほぼ一定値をとるのに対して電子の温度はより大きく変化する.すると
式(9.3.118)の時間変化のスケールは,
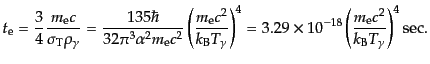 |
(I.3.120) |
となる.赤方偏移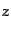 のとき
のとき
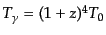 ,
,
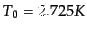 だか
ら,この時間スケールは
だか
ら,この時間スケールは
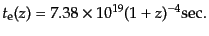 |
(I.3.121) |
となる.例えば
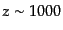 では,
では,
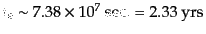 となって,この時点での宇宙年齢
となって,この時点での宇宙年齢
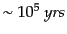 よりも十分短い.宇宙年齢は輻射優勢時
よりも十分短い.宇宙年齢は輻射優勢時
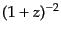 の依存性,物質優
勢時
の依存性,物質優
勢時
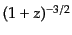 の依存性だから,いずれにしても晴れ上がり以前は宇宙年
齢よりも
の依存性だから,いずれにしても晴れ上がり以前は宇宙年
齢よりも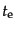 の方が十分短い.こうして光子と物質は強く結合して同
じ温度に保たれるのである.
の方が十分短い.こうして光子と物質は強く結合して同
じ温度に保たれるのである.
次に晴れ上がり以後の宇宙を考えてみる.晴れ上がり以後は電子は陽子と結合
して,中性水素となる.だが,わずかの割合の電子は相手が見付からずに自由
なままとどまる.この自由電子の数の割合を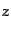 の関数として
の関数として
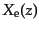 とする.この関数は大まかに式(4.7.70)の解として求まり,十分
とする.この関数は大まかに式(4.7.70)の解として求まり,十分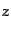 が
小さくなると
が
小さくなると
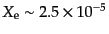 という量になる.自由電子の
数密度
という量になる.自由電子の
数密度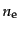 は中性水素の数密度
は中性水素の数密度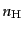 により,
により,
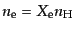 で与えられる.このわずかな自由電子は晴れ上がり後も
背景放射の光子と衝突してエネルギーをやりとりし,また自由電子は他の中性
水素やイオン化原子などと強く相互作用している.結局光子は晴れ上がり以後
も多少は物質と結合していることになる.この効果を見積もってみる.いま物
質の運動エネルギーのほとんどは中性水素によって担われている.そこで中性
水素の数密度を
で与えられる.このわずかな自由電子は晴れ上がり後も
背景放射の光子と衝突してエネルギーをやりとりし,また自由電子は他の中性
水素やイオン化原子などと強く相互作用している.結局光子は晴れ上がり以後
も多少は物質と結合していることになる.この効果を見積もってみる.いま物
質の運動エネルギーのほとんどは中性水素によって担われている.そこで中性
水素の数密度を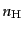 とすると物質のエネルギー密度と圧力は
とすると物質のエネルギー密度と圧力は
| |
|
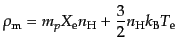 |
(I.3.122) |
| |
|
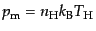 |
(I.3.123) |
としてよい.ここで,中性水素の温度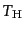 は十分な相互作用により電子の温
度
は十分な相互作用により電子の温
度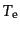 に等しいものと考える.すると,式(9.3.115)から式
(9.3.118)までと同様の計算を繰り返して,
に等しいものと考える.すると,式(9.3.115)から式
(9.3.118)までと同様の計算を繰り返して,
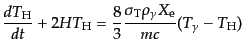 |
(I.3.124) |
を得る.したがって,この場合の温度の時間変化のスケールは
 |
(I.3.125) |
である.この時間変化のスケールが宇宙年齢と比較して短ければ光子のエネル
ギーが物質へ流れ込むことができる.物質優勢期の宇宙年齢は式
(3.6.75)で与えられるので,その条件は
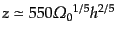 |
(I.3.126) |
よりも以前となる.したがって,宇宙の晴れ上がりの時点
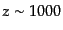 以後も
しばらくは背景放射と物質はほぼ同じ温度で冷却している時期がある.その後
は独立に
以後も
しばらくは背景放射と物質はほぼ同じ温度で冷却している時期がある.その後
は独立に
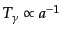 ,
,
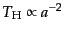 の
ように冷却していくことになる.
の
ように冷却していくことになる.
宇宙の晴れ上がり以後でも,その後の構造形成によって電子の温度が背景放射
よりも十分高い場所ができれば,そこでは逆コンプトン散乱によって背景放射
光子を熱することができる.この現象は実際に,リッチな銀河クラスター中で
実現されていて,そこでは銀河間ガスが高温なプラズマ状態となっている.こ
のように銀河クラスターを通り抜けてきた背景放射光子は平均的なエネルギー
が高くなっている.この効果をスニャーエフ・ゼルドビッチ効果
(Sunyaev-Zel'dovich effect)と呼ぶ.
クラスター中の電子の温度は背景放射の温度よりも十分高温となっているので,
式(9.3.101)の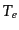 を含む項以外を無視することができ,カンパニエー
ツ方程式(9.3.105)は
を含む項以外を無視することができ,カンパニエー
ツ方程式(9.3.105)は
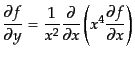 |
(I.3.127) |
と近似される.ここで新たな
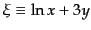 を定義し,独立変数の
組
を定義し,独立変数の
組 を
を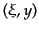 に変換すると,
に変換すると,
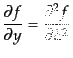 |
(I.3.128) |
となるが,これはよく知られた拡散方程式の形である.一般解はグリーン関数
の方法にフーリエ変換を用いることによって求まり,
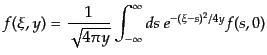 |
(I.3.129) |
で与えられる.独立変数を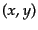 に戻して変数変換すると,
に戻して変数変換すると,
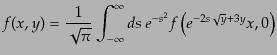 |
(I.3.130) |
となる.これが式(9.3.127)の一般解である.背景放射のスペクトルは
観測的には極めてプランク分布によく一致する.クラスターの外では電子の温
度と光子の温度は等しいから,銀河クラスターへと入って来る背景放射光子の
初期分布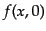 は温度
は温度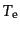 のプランク分布
のプランク分布
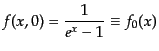 |
(I.3.131) |
としてよい.この初期条件において式(9.3.130)を数値的に積分すれば
クラスターを通り抜けてきた光子の分布関数が求まる.
式(9.3.130)をさらに変形することにより,
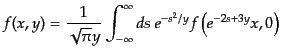 |
(I.3.132) |
となる.ここで,コンプトン化パラメータ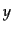 が小さい
が小さい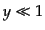 のときはこの
表式に
のときはこの
表式に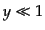 における最急降下法を適用し,近似式を評価することにより,
における最急降下法を適用し,近似式を評価することにより,
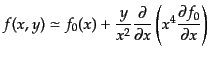 |
(I.3.133) |
を得る.この式は式(9.3.127)からも直接理解できる.したがって,初
期分布の式(9.3.131)により,
となる.光子のエネルギーの小さなレイリー・ジーンズ領域では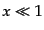 の近
似が成り立ち,このとき
の近
似が成り立ち,このとき
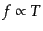 となるから,
となるから,
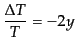 |
(I.3.136) |
となる.これはエネルギーの低い光子が熱い銀河間ガスによってエネルギーの
高い状態へ叩き上げられ,長波長側の光子が減り,有効的な温度が下がってし
まうことを表している.これはあくまで有効温度が下がるのであり,短波長側
では逆に輝度が増えて光子の平均エネルギーは上がっている.つまり黒体放射
スペクトルからずれるのである.
Footnotes
- ...
ルタ関数を2次まで展開することによりI3
- デルタ関数の展開そのもの
には数学的な意味はないが,必ず部分積分をすることを了解しておけば積分後
の式を展開することに等価である.
- ... equation)というI4
- A.S. Kompaneets, Soviet Physics, JETP, 4, 730 (1957)
- ...
を得る.この式はWeymannにより初めて導かれたI5
- R. Weymann, Phys.
Fluids, 8, 2112 (1965)





次へ: トムソン散乱における偏光の取り扱い
上へ: 相対論的運動学
前へ: ボルツマン方程式
目次
索引
All rights reserved © T.Matsubara 2004-2010
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11
![]() ,
, ![]() をそれぞれ
光子と電子の分布関数とし,それぞれ偏極とスピンの自由度にかかわらずに同
じ分布をするものと仮定する.このとき,光子に対する衝突項の形は
をそれぞれ
光子と電子の分布関数とし,それぞれ偏極とスピンの自由度にかかわらずに同
じ分布をするものと仮定する.このとき,光子に対する衝突項の形は
![]() 積分すると、衝突項は部分積分により表面項となっ
て消える.左辺も部分積分することにより,
積分すると、衝突項は部分積分により表面項となっ
て消える.左辺も部分積分することにより,
![]() と陽子
と陽子![]() のプラズマ状
態にあって,お互いに強く相互作用して同じ温度
のプラズマ状
態にあって,お互いに強く相互作用して同じ温度![]() をもつと考える
ことができる.すると,エネルギー密度はそれぞれ
をもつと考える
ことができる.すると,エネルギー密度はそれぞれ
![]() ,
,
![]() で与えられ,圧力は
で与えられ,圧力は
![]() ,
,
![]() で与えられる.したがってプラズマのエネルギー密度と圧力は
で与えられる.したがってプラズマのエネルギー密度と圧力は
![]() .すると光子の光学的厚さ
.すると光子の光学的厚さ
![]() と電子の光学的厚さ
と電子の光学的厚さ
![]() では,
では,
![]() とな
るので,決まった時間内にある電子がまわりの光子に散乱される回数は,ある
光子がまわりの電子に散乱される回数よりも圧倒的に多くなる.したがって,
光子のエネルギー分布関数を変化させることは,電子の分布関数を変化させる
よりもずっと難しくなる.すると,光子は平衡状態からさほどずれていないと
期待できるので,式(4.1.8) による
とな
るので,決まった時間内にある電子がまわりの光子に散乱される回数は,ある
光子がまわりの電子に散乱される回数よりも圧倒的に多くなる.したがって,
光子のエネルギー分布関数を変化させることは,電子の分布関数を変化させる
よりもずっと難しくなる.すると,光子は平衡状態からさほどずれていないと
期待できるので,式(4.1.8) による
![]() の関数として
の関数として
![]() とする.この関数は大まかに式(4.7.70)の解として求まり,十分
とする.この関数は大まかに式(4.7.70)の解として求まり,十分![]() が
小さくなると
が
小さくなると
![]() という量になる.自由電子の
数密度
という量になる.自由電子の
数密度![]() は中性水素の数密度
は中性水素の数密度![]() により,
により,
![]() で与えられる.このわずかな自由電子は晴れ上がり後も
背景放射の光子と衝突してエネルギーをやりとりし,また自由電子は他の中性
水素やイオン化原子などと強く相互作用している.結局光子は晴れ上がり以後
も多少は物質と結合していることになる.この効果を見積もってみる.いま物
質の運動エネルギーのほとんどは中性水素によって担われている.そこで中性
水素の数密度を
で与えられる.このわずかな自由電子は晴れ上がり後も
背景放射の光子と衝突してエネルギーをやりとりし,また自由電子は他の中性
水素やイオン化原子などと強く相互作用している.結局光子は晴れ上がり以後
も多少は物質と結合していることになる.この効果を見積もってみる.いま物
質の運動エネルギーのほとんどは中性水素によって担われている.そこで中性
水素の数密度を![]() とすると物質のエネルギー密度と圧力は
とすると物質のエネルギー密度と圧力は
![]() を含む項以外を無視することができ,カンパニエー
ツ方程式(9.3.105)は
を含む項以外を無視することができ,カンパニエー
ツ方程式(9.3.105)は
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11