




次へ: 量子場の相互作用
上へ: 場の量子化と粒子の相互作用
前へ: 古典的自由場
目次
索引
Subsections
さて、ここまで古典場を見てきた。これら古典場の量子化を行おう。力学的
自由度が無限大ではあるが、通常の量子力学の量子化規則を適用すればよい。
つまり、正準力学変数を演算子とみなし、それらの間に適切な交換関係を設定
することにより量子化が行われる。そして、これらの演算子の作用する空間は
量子的状態に対応することになる。
まず最も簡単な場である実スカラー場の量子化を例にとって、場の量子化の手
続きを詳しく見ていこう。実スカラー場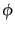 の共役運動量
の共役運動量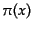 を求め
ると、
を求め
ると、
となる。正準変数に対するポアソン括弧は式(8.2.46)で与えられ、こ
れをある時刻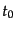 における同時刻交換関係の
における同時刻交換関係の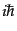 倍で置き換える量子化
規則により量子化される。いまの場合、
倍で置き換える量子化
規則により量子化される。いまの場合、
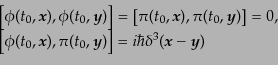 |
(H.5.202) |
である。
これで、場の変数は演算子に置き換えられた。この交換関係をさらに扱いやす
くするため、モード展開(8.4.115)を用いる。運動方程式の解は時刻一
定面において完全系を張っているので、ある時刻一定面上の任意の場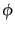 は
は
![$\displaystyle \phi(x) = \int \frac{d^3k}{(2\pi)^3 2k^0} \left[a({\mbox{\boldmath$k$}}) e^{ikx} + a^\dagger({\mbox{\boldmath$k$}}) e^{-ikx} \right]$](img1821.png) |
(H.5.203) |
と展開される。ここで、
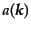 は演算子であるから、式
(8.4.115)における複素共役
は演算子であるから、式
(8.4.115)における複素共役
 はエルミート共役演算子
はエルミート共役演算子
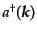 に置き換わっている。基本モードの直交関係
(8.4.114)を使うと、
に置き換わっている。基本モードの直交関係
(8.4.114)を使うと、
![\begin{displaymath}\begin{array}{l} \displaystyle a({\mbox{\boldmath$k$}}) = \le...
...nt d^3x \left[k^0 \phi(x) - ic\pi(x)\right] e^{ikx} \end{array}\end{displaymath}](img1825.png) |
(H.5.204) |
が時刻によらず成り立つから、どの時刻で場を量子化しようともこれらの演算
子の交換関係は同じで、
![\begin{displaymath}\begin{array}{l} \left[ a({\mbox{\boldmath$k$}}), a^\dagger({...
...$}}), a^\dagger({\mbox{\boldmath$k$}}') \right] = 0 \end{array}\end{displaymath}](img1826.png) |
(H.5.205) |
である。この交換関係は、もともとの場の交換関係(8.5.202)と等価で
ある。
場の演算子の作用する状態空間を調べるためには、
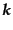 が連続変数のま
まよりも、離散化したほうがわかりやすい。そこで、空間を体積
が連続変数のま
まよりも、離散化したほうがわかりやすい。そこで、空間を体積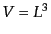 の周
期境界条件を課した立方体と考え、現実の空間は
の周
期境界条件を課した立方体と考え、現実の空間は
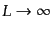 の極
限と考える。すると、一方向あたりの波数ベクトルの間隔は
の極
限と考える。すると、一方向あたりの波数ベクトルの間隔は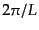 となるか
ら、3次元波数空間の連続的な積分、またデルタ関数は
となるか
ら、3次元波数空間の連続的な積分、またデルタ関数は
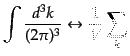 |
|
|
(H.5.206) |
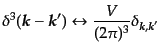 |
|
|
(H.5.207) |
と対応する。
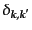 はクロネッカー記号で、
はクロネッカー記号で、
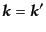 のときのみ
のときのみ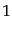 , それ以外はゼロをとる。ここで便宜的
に、離散化された空間での演算子を
, それ以外はゼロをとる。ここで便宜的
に、離散化された空間での演算子を
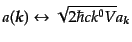 |
(H.5.208) |
と対応させることにすると、展開(8.5.203)は
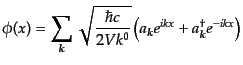 |
(H.5.209) |
となり、交換関係(8.5.205)は
![\begin{displaymath}\begin{array}{l} \left[ a_{\mbox{\scriptsize\boldmath$k$}}, a...
...ger_{{\mbox{\scriptsize\boldmath$k$}}'} \right] = 0 \end{array}\end{displaymath}](img1836.png) |
(H.5.210) |
となる。これをみると、各振動モード
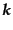 の間に交換関係がなく、かつ、
各々のモードでは調和振動子の昇降演算子と同等の交換関係を持っている。す
なわち、振動モードごとの調和振動子のヒルベルト空間の直積空間が自由場の
状態空間を張ることがわかる。そこで、調和振動子のヒルベルト空間の構成を
そのままなぞって、上の交換関係から導かれる状態空間を構成する。
の間に交換関係がなく、かつ、
各々のモードでは調和振動子の昇降演算子と同等の交換関係を持っている。す
なわち、振動モードごとの調和振動子のヒルベルト空間の直積空間が自由場の
状態空間を張ることがわかる。そこで、調和振動子のヒルベルト空間の構成を
そのままなぞって、上の交換関係から導かれる状態空間を構成する。
あるひとつのモード
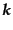 に着目して、つぎの演算子を定義する:
に着目して、つぎの演算子を定義する:
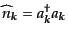 |
(H.5.211) |
ここで、この離散フーリエ空間においてしばらくあるモードのみ考え、添字
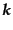 を省略する。この演算子
を省略する。この演算子
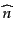 は明らかにエルミートであるので、
その固有値は実数である。さらに固有値が負でない整数
は明らかにエルミートであるので、
その固有値は実数である。さらに固有値が負でない整数
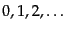 である
ことを以下に示そう。ここで
である
ことを以下に示そう。ここで
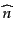 の固有値
の固有値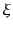 に対応する固有ベクトル
を
に対応する固有ベクトル
を
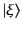 とする:
とする:
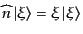 |
(H.5.212) |
固有ベクトル
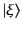 のノルムは正値をとり、ベクトル
のノルムは正値をとり、ベクトル
 のノル
ムは正またはゼロであるから、
のノル
ムは正またはゼロであるから、
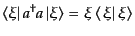 |
(H.5.213) |
により、
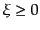 であることが結論される。
ここで、交換関係(8.5.210)を使うと、
であることが結論される。
ここで、交換関係(8.5.210)を使うと、
![$\displaystyle \left[\widehat{n},a\right] = -a,\qquad \left[\widehat{n},a^\dagger\right] = a^\dagger$](img1845.png) |
(H.5.214) |
である。したがって、
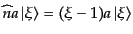 |
(H.5.215) |
となり、
 も
も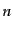 の固有ベクトルで、固有値は
の固有ベクトルで、固有値は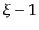 に対応する。
つまり、演算子
に対応する。
つまり、演算子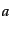 は固有値を
は固有値を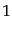 だけ下げる働きがある。ここで、もし
だけ下げる働きがある。ここで、もし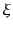 が整数でなければ、何度も
が整数でなければ、何度も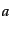 を
を
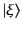 に作用させることによって負の固
有値に属する固有ベクトルを作り出すことができてしまい、上で導いた固有値
の正値性に矛盾する。こうして、
に作用させることによって負の固
有値に属する固有ベクトルを作り出すことができてしまい、上で導いた固有値
の正値性に矛盾する。こうして、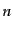 の固有値は負でない整数であることが証
明された。
の固有値は負でない整数であることが証
明された。
また、同様に交換関係(8.5.210)から
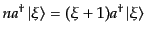 |
(H.5.216) |
となり、演算子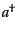 は固有値を
は固有値を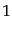 だけ上げる働きがある。
だけ上げる働きがある。
固有値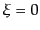 に対応する固有ベクトルを
に対応する固有ベクトルを
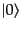 と書くことにし、
と書くことにし、
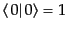 と規格化されているものとする。このベクトルは
と規格化されているものとする。このベクトルは
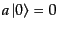 |
(H.5.217) |
を満たす。そうでなければ負の固有値に導かれてしまうからである。すると、
この最低固有値に属する固有ベクトルに演算子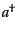 を
を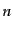 回作用させれ
ば固有値
回作用させれ
ば固有値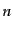 に対応する固有ベクトル
に対応する固有ベクトル
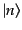 ができる。規格化を
ができる。規格化を
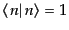 となるように取れば、
となるように取れば、
 |
(H.5.218) |
であることがわかる。この規格化因子は交換関係(8.5.214)を繰り返し
使うことにより導かれる。
以上のヒルベルト空間をあらゆるモードについて直積をとれば、実スカラー場
の量子論的状態空間が構成される。一般の状態は、
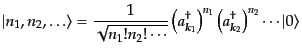 |
(H.5.219) |
によって張られる基底の線形結合で表される。ここで基底状態
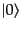 はす
べての波数について
はす
べての波数について
 を満たすような状態として定義さ
れる。上の基底をフォック基底(Fock base), また、その基底の張る線
形空間をフォック空間 (Fock space)と呼び、それは自由場の量子的状
態空間である。
を満たすような状態として定義さ
れる。上の基底をフォック基底(Fock base), また、その基底の張る線
形空間をフォック空間 (Fock space)と呼び、それは自由場の量子的状
態空間である。
さて、式(8.2.49)で与えられる全4元運動量の添字を上げたものは、
と計算される。これを離散化した波数空間の和で書き直し、さらに交換関係
(8.5.210)を使うと、
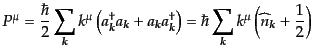 |
(H.5.221) |
空間成分
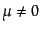 に対しては最後の
に対しては最後の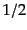 の項は
の項は
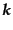 の和の対称性か
ら消える。すると、固有状態(8.5.219)に上の演算子の空間成分を作用
させてみると、
の和の対称性か
ら消える。すると、固有状態(8.5.219)に上の演算子の空間成分を作用
させてみると、
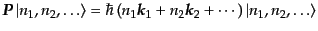 |
(H.5.222) |
となる。したがって、
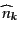 の固有状態
の固有状態
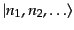 は
は
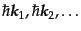 という3次元運動量を持つ粒
子数がそれぞれ
という3次元運動量を持つ粒
子数がそれぞれ
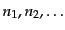 であるような状態に対応しているという解
釈が成り立つ。したがって、演算子
であるような状態に対応しているという解
釈が成り立つ。したがって、演算子
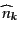 は運動量
は運動量
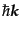 の粒子の個数を与える演算子と解釈され、個数演算子
(number operator)と呼ばれる。すると、基底状態
の粒子の個数を与える演算子と解釈され、個数演算子
(number operator)と呼ばれる。すると、基底状態
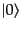 は粒子のない真
空状態である。さらに、演算子
は粒子のない真
空状態である。さらに、演算子
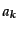 は運動量
は運動量
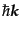 の粒子
の個数を一つ減らす演算子であり、消滅演算子 (annihilation
operator)、また、
の粒子
の個数を一つ減らす演算子であり、消滅演算子 (annihilation
operator)、また、
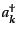 は粒子の個数を一つ増やす演算子で
あり、生成演算子 (creation operator)と呼ばれる。このように、場を
量子化することによって、粒子の描像が現れてくるのである。
は粒子の個数を一つ増やす演算子で
あり、生成演算子 (creation operator)と呼ばれる。このように、場を
量子化することによって、粒子の描像が現れてくるのである。
一方、式(8.5.221)の時間成分に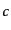 をかけたものは場の全エネルギー
であるが、この場合には
をかけたものは場の全エネルギー
であるが、この場合には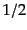 の項も消えずに残ってしまう。
の項も消えずに残ってしまう。
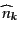 の真空期待値は
の真空期待値は
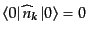 であるから、この残りの項はエネルギーの真空期待値に対応する。
これはちょうど調和振動子でのゼロ点エネルギーに対応するもので、波数によ
る和は発散を導いてしまう。この発散項は連続変数の表示では、
であるから、この残りの項はエネルギーの真空期待値に対応する。
これはちょうど調和振動子でのゼロ点エネルギーに対応するもので、波数によ
る和は発散を導いてしまう。この発散項は連続変数の表示では、
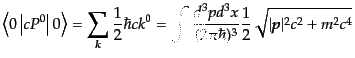 |
(H.5.223) |
となる。ここで、波数ベクトル
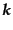 の積分は運動量
の積分は運動量
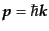 の積分で書きなおした。これをみると明らかなように、単位位相体積
の積分で書きなおした。これをみると明らかなように、単位位相体積
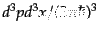 あたりにゼロ点振動のエネルギー
あたりにゼロ点振動のエネルギー
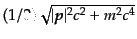 がひとつずつ寄与している。真空状態の
エネルギーが発散していると都合が悪いが、これは定数であるので、エネルギー
の原点をずらして、
がひとつずつ寄与している。真空状態の
エネルギーが発散していると都合が悪いが、これは定数であるので、エネルギー
の原点をずらして、
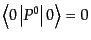 となるように
となるように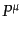 の定義を変
える:
の定義を変
える:
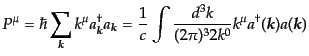 |
(H.5.224) |
特にハミルトニアンは、
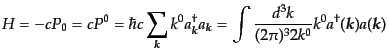 |
(H.5.225) |
である。こうするとエネルギーの基底状態での値はゼロになる。
この方法では、あとから都合の良いように手でエネルギーの基準値を変えたよ
うに見えるが、そのような操作は許されるのだろうか? 上であらわれてきた
発散項はもともと生成消滅演算子の交換関係から生じている。古典論の段階で
はあらゆる量は交換するので、もし、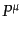 を古典論においてて
を古典論においてて
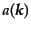 ,
,
 で表し、それを表式を量子論に移行したと考え
るとこれらの演算子順序について不定性があることになる。そこで、場の積で
与えられる量については量子化するときに必ず生成演算子は消滅演算子の左に
くるという正規順序 (normal ordering)をとることにすれば、発散する
基底エネルギーは現れない。正規順序はコロンで囲まれた記号
で表し、それを表式を量子論に移行したと考え
るとこれらの演算子順序について不定性があることになる。そこで、場の積で
与えられる量については量子化するときに必ず生成演算子は消滅演算子の左に
くるという正規順序 (normal ordering)をとることにすれば、発散する
基底エネルギーは現れない。正規順序はコロンで囲まれた記号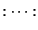 で表
され、例えばいまの例では
で表
され、例えばいまの例では
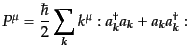 |
(H.5.226) |
である。このような規約をとれば発散エネルギーは表われてこないようにでき
るが、もともと基本的な場の量は実空間の演算子であると考えられるので、上
の規約が自然なものと言えたわけではない。だが、理論に矛盾がない限りにお
いてこの規約を認めてすすんでもよいであろう。エネルギーの基準値は実験的
には観測されるものではないので、実際に問題とはならないH5 。
このような規約のもとで、フォック基底は
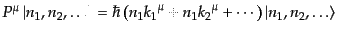 |
(H.5.227) |
となり、フォック基底は、4元運動量
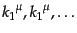 を持つ
粒子がそれぞれ
を持つ
粒子がそれぞれ
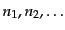 個ずつあるという意味を持つことになる。
この結果はラグランジアンが場の2次のみで書かれる自由場であったからこそ
可能で、運動方程式が場について線形であることが本質的である。一般に相互
作用のある系では運動方程式が非線形になり、上のような簡明な描像を得るこ
とは難しい。
個ずつあるという意味を持つことになる。
この結果はラグランジアンが場の2次のみで書かれる自由場であったからこそ
可能で、運動方程式が場について線形であることが本質的である。一般に相互
作用のある系では運動方程式が非線形になり、上のような簡明な描像を得るこ
とは難しい。
自由場の場合、フーリエ変換の形(8.4.115)のように解けているので、
同時刻でない任意の2点での場の交換関係を導くことが可能である。演算子と
してのフーリエ展開
![$\displaystyle \phi(x) = \int \frac{d^3k}{(2\pi)^3 2k^0} \left[a({\mbox{\boldmath$k$}}) e^{ikx} + a^\dagger({\mbox{\boldmath$k$}}) e^{-ikx} \right]$](img1821.png) |
(H.5.228) |
により、
![$\displaystyle \left[\phi(x), \phi(y)\right] = \hbar c \int \frac{d^3k}{(2\pi)^3 2k^0} \left( e^{ik(x-y)} - e^{-ik(x-y)}\right) \equiv i\hbar c {\mit\Delta}(x-y)$](img1884.png) |
(H.5.229) |
である。この関数
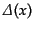 を不変デルタ関数という。ここで、符合関数
を不変デルタ関数という。ここで、符合関数
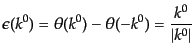 |
(H.5.230) |
を使うと、
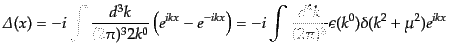 |
(H.5.231) |
と表されるので、この関数はローレンツ不変な奇関数であることが明らかであ
る。また、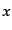 が空間的ベクトルであれば、
が空間的ベクトルであれば、
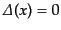 となる。これを見
るには、空間的ベクトルはローレンツ変換によって必ず
となる。これを見
るには、空間的ベクトルはローレンツ変換によって必ず
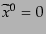 と
することができ、さらに座標の回転を行って座標
と
することができ、さらに座標の回転を行って座標
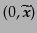 は、
は、
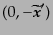 に移すことができることに注意する。座標回転もロー
レンツ変換の一種である。すると、ローレンツ不変性と奇関数であることから、
に移すことができることに注意する。座標回転もロー
レンツ変換の一種である。すると、ローレンツ不変性と奇関数であることから、
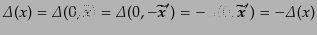 |
(H.5.232) |
となり、結局ゼロであることがわかる。量子論的な物理量はお互いに干渉しあ
うことなしに観測されるならば可換である。空間的に離れた2点の場の量が可
換であることは、光速度よりも早く伝わる経路でしかつながらない2点はお互
いに干渉しないことを意味する。これは微視的な因果律を表す。また、不変デ
ルタ関数はクライン・ゴルドン方程式を満たし、さらに、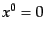 において
において
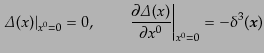 |
(H.5.233) |
であることがわかる。
上で与えた量子化の手続きは他の場についてもほとんど同様であるので、以下
には要点のみ見ていこう。複素スカラー場の場合、実スカラー場にない特徴と
して保存荷を持っているという違いがある。複素場は2自由度を持つので、
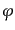 とその複素共役
とその複素共役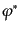 を独立な場として扱うことにすると、
それぞれの共役運動量は
を独立な場として扱うことにすると、
それぞれの共役運動量は
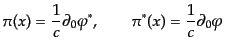 |
(H.5.234) |
となる。量子化は、
![$\displaystyle \left[\phi(t_0,{\mbox{\boldmath$x$}}), \pi(t_0,{\mbox{\boldmath$y...
...$y$}}) \right] = i\hbar \delta^3({\mbox{\boldmath$x$}} - {\mbox{\boldmath$y$}})$](img1896.png) |
(H.5.235) |
となる。ただし、他の同時刻交換関係はすべてゼロにおく。場の展開は
| |
|
![$\displaystyle \phi(x) = \int \frac{d^3k}{(2\pi)^3 2k^0}
\left[a({\mbox{\boldmath$k$}}) e^{ikx} +
b^\dagger({\mbox{\boldmath$k$}}) e^{-ikx} \right]$](img1897.png) |
(H.5.236) |
| |
|
![$\displaystyle \phi^\dagger(x) = \int \frac{d^3k}{(2\pi)^3 2k^0}
\left[b({\mbox{\boldmath$k$}}) e^{ikx} +
a^\dagger({\mbox{\boldmath$k$}}) e^{-ikx} \right]$](img1898.png) |
(H.5.237) |
であり、ここから生成消滅演算子の交換関係は
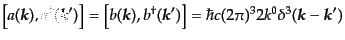 |
(H.5.238) |
となり、他の組み合わせはすべて交換する。ここで、場の自由度が2であるこ
とに対応して2種類の生成消滅演算子がある。そこで基底状態
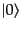 はすべ
ての
はすべ
ての
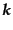 について
について
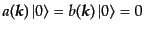 |
(H.5.239) |
を満たすものと定義される。実スカラー場の場合と全く同様の議論により、正
規順序を考慮して全4元運動量は
![$\displaystyle P^\mu = \frac1{c} \int \frac{d^3k}{(2\pi)^3 2 k^0} k^\mu \left[ a...
...dmath$k$}}) + b^\dagger({\mbox{\boldmath$k$}}) b({\mbox{\boldmath$k$}}) \right]$](img1901.png) |
(H.5.240) |
となる。
次に式(8.4.120)のネーターカレントを考えよう。これは量子化された
場に対しては
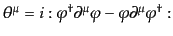 |
|
|
(H.5.241) |
で与えられる。そこで、保存荷(8.4.121)を生成消滅演算子で表せば、
となる。ここからわかるように、2種類の生成消滅演算子で表される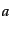 -粒子
と
-粒子
と -粒子は保存荷について反対符合で寄与している。この符合の違いを別に
すれば全く同じ性質を持つ粒子に対応する。この性質は複素スカラー場の場合
のみでなく一般的な性質である。つまり、対称性に起因する保存荷を持った粒
子がある場合、一般的に質量やその他の性質は全く同一だが、保存荷だけが反
対符合となる反粒子が必ず存在するのである。
-粒子は保存荷について反対符合で寄与している。この符合の違いを別に
すれば全く同じ性質を持つ粒子に対応する。この性質は複素スカラー場の場合
のみでなく一般的な性質である。つまり、対称性に起因する保存荷を持った粒
子がある場合、一般的に質量やその他の性質は全く同一だが、保存荷だけが反
対符合となる反粒子が必ず存在するのである。
スピノル場の量子化の例としてディラック場の量子化をみてみよう。スカラー
場との大きな違いはスピノル場がフェルミ粒子を表すために古典場としてはグ
ラスマン数であり、量子化に際して交換関係ではなく反交換関係が課される。
これは経験的に知られているパウリの排他律を満たすためには必要な変更であ
る。ディラック場におけるラグランジアン(8.4.156)から共役運動量変
数を求めれば、
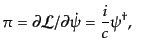 |
(H.5.243) |
となり、
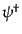 は実質的に
は実質的に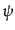 の共役運動量変数であることがわか
る。ここで、量子化を反交換関係
の共役運動量変数であることがわか
る。ここで、量子化を反交換関係
![$ [a,b]_+ \equiv ab + ba$](img1908.png) により行う。つま
り、次の同時刻反交換関係
により行う。つま
り、次の同時刻反交換関係
| |
|
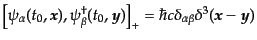 |
(H.5.244) |
| |
|
![$\displaystyle \left[\psi_\alpha(t_0,{\mbox{\boldmath$x$}}),
\psi_\beta(t_0,{\m...
...x{\boldmath$x$}}),
\psi^\dagger_\beta(t_0,{\mbox{\boldmath$y$}})\right]_+
= 0$](img1910.png) |
(H.5.245) |
を設定するH6。スピノル場の平面波展開は
となるから、生成消滅演算子については次の反交換関係
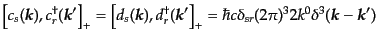 |
(H.5.248) |
が課せられ、他の組合わせはすべて反交換する。基底状態はすべて
の 、
、
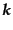 について
について
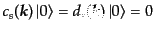 |
(H.5.249) |
で定義される。さて、保存量について有限の真空期待値を得るためには正規順
序積をとることが必要であったが、フェルミ粒子の場合にはその定義に変更が
必要で、演算子の順序を交換するときにマイナスの符合をつけることになる。
例えば、
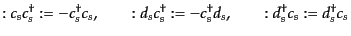 |
(H.5.250) |
などとなる。つまり、あらゆる量は反交換するかのようにして生成演算子を消
滅演算子の前に持ってくるのである。すると、全4元運動量は
![$\displaystyle P^\mu = \hbar \int \frac{d^3k}{(2\pi)^3 2 k^0} k^\mu \sum_{s=\pm ...
...h$k$}}) + d_s^\dagger({\mbox{\boldmath$k$}}) d_s({\mbox{\boldmath$k$}}) \right]$](img1918.png) |
(H.5.251) |
また、(8.4.148)の保存荷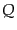 は
は
となる。ここでも、粒子と反粒子の対応が見て取れる。このディラック場が電
子の場を表すならば、2種類の粒子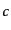 -粒子と
-粒子と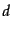 -粒子は電子と陽電子に対応
する。
-粒子は電子と陽電子に対応
する。
次にベクトル場の量子化を考える。一般にゲージ場の正準形式は拘束系となり、
その量子化は他の場合に比べて特別の注意が必要である。ここでは最も簡単な
ベクトル場である電磁場、すなわち質量ゼロの可換ゲージ場をとくに考えるこ
とにする。電磁場における自由ベクトル場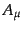 のラグランジアンは
のラグランジアンは
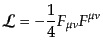 |
(H.5.253) |
で与えられ、ここから共役運動量変数を求めると、
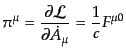 |
(H.5.254) |
となる。左辺は反対称テンソルであるから、残念ながら恒等的に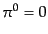 となる。したがって時間成分に対して正準交換関係を設定することができない
ことになってしまう。これは一般にゲージ場の量子化が一筋縄でいかないこと
の現れであるが、電磁場の場合、この困難は次のようにして、比較的簡単な処
方で避けることができる。まずラグランジアンを次の形に変更する:
となる。したがって時間成分に対して正準交換関係を設定することができない
ことになってしまう。これは一般にゲージ場の量子化が一筋縄でいかないこと
の現れであるが、電磁場の場合、この困難は次のようにして、比較的簡単な処
方で避けることができる。まずラグランジアンを次の形に変更する:
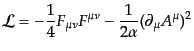 |
(H.5.255) |
ここで、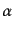 は任意のパラメータである。ローレンツゲージ条件
は任意のパラメータである。ローレンツゲージ条件
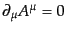 のもとではこのラグランジアンはもとのラグランジ
アン(8.5.253)に等しい。つまり、このラグランジアンはローレンツゲー
ジ条件を拘束としてラグランジュ未定項を導入したことになっている。この項
をゲージ固定項 (gauge fixing term)と呼ぶ。ただしこの後詳しく見る
ように、量子論ではこのような拘束条件を演算子に対して課すことはできない
ことが示されるので、この変形されたラグランジアンから出発し、パラメータ
のもとではこのラグランジアンはもとのラグランジ
アン(8.5.253)に等しい。つまり、このラグランジアンはローレンツゲー
ジ条件を拘束としてラグランジュ未定項を導入したことになっている。この項
をゲージ固定項 (gauge fixing term)と呼ぶ。ただしこの後詳しく見る
ように、量子論ではこのような拘束条件を演算子に対して課すことはできない
ことが示されるので、この変形されたラグランジアンから出発し、パラメータ
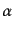 は自由に選べるものとする。このラグランジアンから運動方程式を
求めると、
は自由に選べるものとする。このラグランジアンから運動方程式を
求めると、
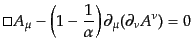 |
(H.5.256) |
となる。ここで、
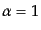 と選べばローレンツゲージ条件を満たす場合の
運動方程式
と選べばローレンツゲージ条件を満たす場合の
運動方程式
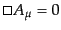 |
(H.5.257) |
に一致し、計算が簡単になるので、以下、
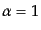 を採用する。この選択
はファインマンゲージ (Feynman gauge)と呼ばれる。このときラグラン
ジアン(8.5.255)を書き直して発散で表される全微分項を落とすと、
を採用する。この選択
はファインマンゲージ (Feynman gauge)と呼ばれる。このときラグラン
ジアン(8.5.255)を書き直して発散で表される全微分項を落とすと、
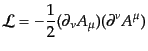 |
(H.5.258) |
となる。すると共役運動量変数は
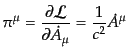 |
(H.5.259) |
であるから、同時刻交換関係は
![\begin{displaymath}\begin{array}{l} \left[A^\mu(t_0, {\mbox{\boldmath$x$}}), \do...
... \dot{A}^\nu(t_0, {\mbox{\boldmath$y$}})\right] = 0 \end{array}\end{displaymath}](img1931.png) |
(H.5.260) |
となる。ここで、ベクトル場の4つの成分は質量なしのクラインゴルドン方程
式(8.5.257)を満たし、交換関係は独立にスカラー場の交換関係と類似
のものとなっているので、スカラー場の量子化の手続きはほとんどそのまま用
いられる。ただし、空間成分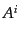 はまさにスカラー場の交換関係と同一であ
るが、時間成分
はまさにスカラー場の交換関係と同一であ
るが、時間成分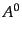 は交換関係の右辺の符合が逆になっている!このことは
スカラー場の量子化をそのまま使えないことを意味するが、下に見るように技
術的な問題であり、物理的に意味がなくなるような問題ではない。
は交換関係の右辺の符合が逆になっている!このことは
スカラー場の量子化をそのまま使えないことを意味するが、下に見るように技
術的な問題であり、物理的に意味がなくなるような問題ではない。
ベクトル場の平面波展開は
![$\displaystyle A^\mu = \int \frac{d^3k}{(2\pi)^3 2k^0} \sum_{\lambda=0}^3 \left[...
...dmath$k$}}){\varepsilon_\lambda}^{\mu*}({\mbox{\boldmath$k$}}) e^{-ikx} \right]$](img1788.png) |
(H.5.261) |
であり、ここから生成消滅演算子の交換関係を求めると、
![\begin{displaymath}\begin{array}{l} \left[a_\lambda({\mbox{\boldmath$k$}}), a_{\...
...agger_{\lambda'}({\mbox{\boldmath$k$}}')\right] = 0 \end{array}\end{displaymath}](img1934.png) |
(H.5.262) |
となる。ここで、時間成分の交換関係がスカラー場と逆符合であったため、ス
カラー偏極成分の生成消滅演算子
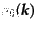 ,
,
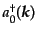 の
交換関係の符合がスカラー場の場合と逆になってしまっている。
の
交換関係の符合がスカラー場の場合と逆になってしまっている。
また、全4元運動量をスカラー場の場合と同様にして計算すると、
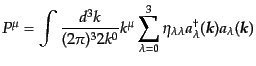 |
(H.5.263) |
となって、スカラー偏極成分の粒子はエネルギーや運動量に逆の符合で寄与し
ていて奇妙なことになっている。ともかくもここに得られた生成消滅演算子を
用いてフォック空間を作ってみる。スカラー場の場合と同様に、離散化した演
算子を用いて、基底状態
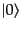 をすべての
をすべての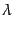 ,
,
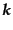 に対して
に対して
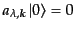 ,
,
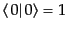 を満たす
ものと定義する。すると、一粒子状態のノルムは
を満たす
ものと定義する。すると、一粒子状態のノルムは
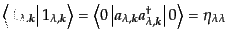 |
(H.5.264) |
となるので、スカラー偏極成分のヒルベルト空間のノルムは負になってしまう。
このことは量子論の確率解釈において負の確率を導くこととなってしまい、こ
れは物理的な存在とみなすことはできない。
このようにスカラー偏極成分は物理的には奇妙な存在であるが、実際には光子
には横偏極成分しか観測されない。そもそも光子の物理的自由度は2であり、
横偏極成分以外は非物理的なものである。にもかかわらずこのような非物理的
な自由度が現れているのは、量子化に際してまだゲージ固定がなされていない
からである。我々はローレンツゲージのもとでマックスウェル方程式に等価な
ラグランジアン(8.5.258)から出発してはいるが、まだ量子化に際して
このゲージ固定がなされていないので4自由度が残っているのである。だが、
演算子の段階でローレンツゲージ条件を課すと矛盾に導かれる。実際、場の同
時刻交換関係から、
![$\displaystyle \left[\partial_\mu A^\mu(t,{\mbox{\boldmath$x$}}), A^\nu(t,{\mbox...
...t] = -i\hbar c\eta^{0\nu} \delta^3({\mbox{\boldmath$x$}}-{\mbox{\boldmath$y$}})$](img1940.png) |
(H.5.265) |
となるので、演算子として恒等的にローレンツゲージ条件
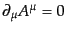 を成立させることはできない。
を成立させることはできない。
こうして、ローレンツゲージ条件を演算子に対して課すことは許されないこと
がわかる。だが、演算子そのものとしてゲージ条件が成り立つことは必ずしも
必要ではなく、より弱い関係として、ヒルベルト空間に対する付加条件として
成り立つものと考えることが可能である。このようにすれば負ノルムが物理的
な観測量に現れることはなくなる。この方法はグプタ・ブロイラーの方
法 (Gupta-Bleuler method)と呼ばれるものである。この方法では、物理的な
ヒルベルト空間の状態ベクトル
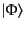 に対して、付加条件
に対して、付加条件
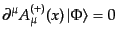 |
(H.5.266) |
を課す。ここで、
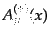 は展開式(8.4.192)において消滅
演算子を含んだ正振動部分のことである。負振動部分は
は展開式(8.4.192)において消滅
演算子を含んだ正振動部分のことである。負振動部分は
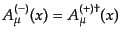 で与えられ、
で与えられ、
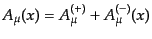 である。この分解は相対論的に不
変な分解となっている
H7。条件
(8.5.266)とその共役
である。この分解は相対論的に不
変な分解となっている
H7。条件
(8.5.266)とその共役
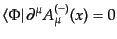 |
(H.5.267) |
により、ローレンツゲージ条件は物理的状態ベクトルによる期待値の意味で常
に成り立つ:
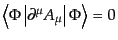 |
(H.5.268) |
したがって、古典極限ではローレンツゲージ条件が成立して、マックスウェル
方程式が成り立つこととなる。
付加条件(8.5.266)を展開(8.4.192)を使って書き直す。横偏
極の定義式(8.4.198)を使い、また
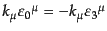 であることを使うと、この付加条件に同値な条件と
して、すべての
であることを使うと、この付加条件に同値な条件と
して、すべての
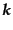 について
について
![$\displaystyle \left[a_0({\mbox{\boldmath$k$}}) - a_3({\mbox{\boldmath$k$}})\right]\left\vert \Phi \right\rangle = 0$](img1951.png) |
(H.5.269) |
となることがわかる。この結果、縦偏極光子とスカラー偏極光子の数は、物理
的状態空間における期待値としては等しくなる:
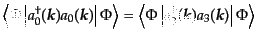 |
(H.5.270) |
すると全4元運動量の表式(8.5.263)において、物理的状態空間にお
ける期待値を取る限り、スカラー偏極光子は正の符合で寄与する縦偏極光子と
必ず消ち消しあって、負エネルギー粒子が現れることはなくなる:
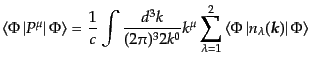 |
(H.5.271) |
ここで、
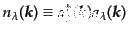 は連続極限での個数演算子である。横偏極光子のみが実
質的にエネルギーや運動量に寄与することになる。
は連続極限での個数演算子である。横偏極光子のみが実
質的にエネルギーや運動量に寄与することになる。
このようにフォック空間を構成すると、スカラー偏極光子と縦偏極光子がいく
ら含まれようとも物理的に等価な状態を表すことになる。これは非物理的な自
由度がさらにまだ残っていることを意味するが、これはよく知られているよう
に古典論でローレンツゲージが完全に非物理的自由度を固定しないことに対応
している。観測される光子は物理的な横偏極成分しか存在しない。だが、この
あと摂動論において具体的に見るように、粒子の反応の中間段階に出現する、
観測されることのない仮想光子においては縦偏極やスカラー偏極の光子は無視
することのできない重要な自由度として現れてくる。
Footnotes
- ...
には観測されるものではないので、実際に問題とはならないH5
- 実は、
これには重大な例外がある。一般相対論において、エネルギーの基準値である
真空エネルギーの値は時空を曲げることになり、平坦な時空が存在できなくなっ
てしまうのである。これは現在のところ、未解決な問題となっている。
- ...
を設定するH6
- 本来は拘束系の正準形式から導かれるべきであるが、結
局は同じ結果になる。
- ...
変な分解となっているH7
-
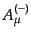 は生成演算子を含んでいるので、
は生成演算子を含んでいるので、
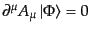 という付加条件を課すことはできない。
という付加条件を課すことはできない。





次へ: 量子場の相互作用
上へ: 場の量子化と粒子の相互作用
前へ: 古典的自由場
目次
索引
All rights reserved © T.Matsubara 2004-2010
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11
![]() の共役運動量
の共役運動量![]() を求め
ると、
を求め
ると、
![]() は
は
![]() が連続変数のま
まよりも、離散化したほうがわかりやすい。そこで、空間を体積
が連続変数のま
まよりも、離散化したほうがわかりやすい。そこで、空間を体積![]() の周
期境界条件を課した立方体と考え、現実の空間は
の周
期境界条件を課した立方体と考え、現実の空間は
![]() の極
限と考える。すると、一方向あたりの波数ベクトルの間隔は
の極
限と考える。すると、一方向あたりの波数ベクトルの間隔は![]() となるか
ら、3次元波数空間の連続的な積分、またデルタ関数は
となるか
ら、3次元波数空間の連続的な積分、またデルタ関数は
![]() に着目して、つぎの演算子を定義する:
に着目して、つぎの演算子を定義する:
![]() に対応する固有ベクトルを
に対応する固有ベクトルを
![]() と書くことにし、
と書くことにし、
![]() と規格化されているものとする。このベクトルは
と規格化されているものとする。このベクトルは
![]() に対しては最後の
に対しては最後の![]() の項は
の項は
![]() の和の対称性か
ら消える。すると、固有状態(8.5.219)に上の演算子の空間成分を作用
させてみると、
の和の対称性か
ら消える。すると、固有状態(8.5.219)に上の演算子の空間成分を作用
させてみると、
![]() をかけたものは場の全エネルギー
であるが、この場合には
をかけたものは場の全エネルギー
であるが、この場合には![]() の項も消えずに残ってしまう。
の項も消えずに残ってしまう。
![]() の真空期待値は
の真空期待値は
![]() であるから、この残りの項はエネルギーの真空期待値に対応する。
これはちょうど調和振動子でのゼロ点エネルギーに対応するもので、波数によ
る和は発散を導いてしまう。この発散項は連続変数の表示では、
であるから、この残りの項はエネルギーの真空期待値に対応する。
これはちょうど調和振動子でのゼロ点エネルギーに対応するもので、波数によ
る和は発散を導いてしまう。この発散項は連続変数の表示では、
![]() を古典論においてて
を古典論においてて
![]() ,
,
![]() で表し、それを表式を量子論に移行したと考え
るとこれらの演算子順序について不定性があることになる。そこで、場の積で
与えられる量については量子化するときに必ず生成演算子は消滅演算子の左に
くるという正規順序 (normal ordering)をとることにすれば、発散する
基底エネルギーは現れない。正規順序はコロンで囲まれた記号
で表し、それを表式を量子論に移行したと考え
るとこれらの演算子順序について不定性があることになる。そこで、場の積で
与えられる量については量子化するときに必ず生成演算子は消滅演算子の左に
くるという正規順序 (normal ordering)をとることにすれば、発散する
基底エネルギーは現れない。正規順序はコロンで囲まれた記号![]() で表
され、例えばいまの例では
で表
され、例えばいまの例では
![]() とその複素共役
とその複素共役![]() を独立な場として扱うことにすると、
それぞれの共役運動量は
を独立な場として扱うことにすると、
それぞれの共役運動量は
![]() のラグランジアンは
のラグランジアンは
![]() に対して、付加条件
に対して、付加条件
![]() であることを使うと、この付加条件に同値な条件と
して、すべての
であることを使うと、この付加条件に同値な条件と
して、すべての
![]() について
について
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11