




次へ: 古典的自由場
上へ: 場の量子化と粒子の相互作用
前へ: 場の理論の正準形式
目次
索引
Subsections
ここまで一般の場について考えてきたが、具体的にはどのような場があるのだ
ろうか? 実は、場は際限なくどのようなものでも許されるわけではなく、特
殊相対論に矛盾しないようにすると、その性質は強く制限される。この節では、
それがどのようなものであるかを見る。この節では、局所ミンコフスキー空間
を考え、計量は
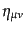 であるとする。
であるとする。
ローレンツ変換
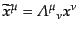 |
(H.3.54) |
を考える。ここで、
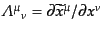 はローレンツ変換を表す行列で、
はローレンツ変換を表す行列で、
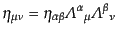 |
(H.3.55) |
を満たす。ローレンツ変換を2度行えば、さらに異なった座標系へ移るが、こ
れはもとの座標からの一度のローレンツ変換で移ることができる。これはすな
わち、ローレンツ変換が群 (group)をなすことを意味する。群Gとは、
要素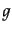 の集合であり、ある群の任意の2つの要素
の集合であり、ある群の任意の2つの要素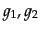 の間に積
の間に積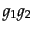 が定義され、その積もまたその群に属するようなものであり、さらに、積
は結合性(associative)を持つものである。結合性とは、
が定義され、その積もまたその群に属するようなものであり、さらに、積
は結合性(associative)を持つものである。結合性とは、
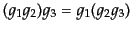 を満たすことである。さらに、群には
を満たすことである。さらに、群には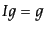 を満たすよう
な単位元(identity)
を満たすよう
な単位元(identity) が存在し、また、群の任意の要素
が存在し、また、群の任意の要素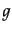 に対して
に対して
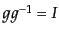 となるような逆元
となるような逆元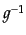 が存在する。
が存在する。
ローレンツ変換の変換行列について、
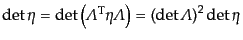 |
(H.3.56) |
であるから、
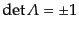 |
(H.3.57) |
を満たす。
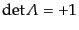 のとき、このローレンツ変換は固有ロー
レンツ変換 (proper Lorentz transformation)と呼ばれる。他方、
のとき、このローレンツ変換は固有ロー
レンツ変換 (proper Lorentz transformation)と呼ばれる。他方、
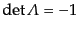 のときは、非固有ローレンツ変換 (improper
Lorentz transformation)と呼ばれる。固有ローレンツ変換であるローレンツ
群の要素と、非固有ローレンツ変換でなる要素はお互いに連続的な変換では移
り得ない。このように連続的につながっていない群の成分を、非連結な成分と
いう。さらに、式(8.3.55)の
のときは、非固有ローレンツ変換 (improper
Lorentz transformation)と呼ばれる。固有ローレンツ変換であるローレンツ
群の要素と、非固有ローレンツ変換でなる要素はお互いに連続的な変換では移
り得ない。このように連続的につながっていない群の成分を、非連結な成分と
いう。さらに、式(8.3.55)の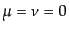 成分により、
成分により、
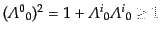 |
(H.3.58) |
であるから、
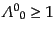 の成分と
の成分と
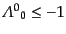 の成分も
非連結である。前者に属するローレンツ変換は順時間的
(orthochronous)であるといわれ、後者に属するものは逆時間的
(anti-orthochronous)といわれる。
の成分も
非連結である。前者に属するローレンツ変換は順時間的
(orthochronous)であるといわれ、後者に属するものは逆時間的
(anti-orthochronous)といわれる。
こうして、ローレンツ群は、都合4つの連結成分に分類される。ローレンツ群
の単位元
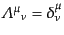 、つまり、何もしない変換に
連結な成分は順時間的固有ローレンツ変換である。これは、本義ローレ
ンツ変換とも呼ばれる。その他の非連結な成分は、時間反転、および空間反
転によって移り変わることができる。事実、時間反転は順時間的変換を逆時間
的にし、また、空間反転は固有ローレンツ変換を非固有ローレンツ変換にする
ことが明らかである。特殊相対論の要請を満たすには、本義ローレンツ変換の
もとで理論が不変であればよく、時間反転や空間反転の不変性については必ず
しも成り立ってなくてもよい。
、つまり、何もしない変換に
連結な成分は順時間的固有ローレンツ変換である。これは、本義ローレ
ンツ変換とも呼ばれる。その他の非連結な成分は、時間反転、および空間反
転によって移り変わることができる。事実、時間反転は順時間的変換を逆時間
的にし、また、空間反転は固有ローレンツ変換を非固有ローレンツ変換にする
ことが明らかである。特殊相対論の要請を満たすには、本義ローレンツ変換の
もとで理論が不変であればよく、時間反転や空間反転の不変性については必ず
しも成り立ってなくてもよい。
ローレンツ変換は、変換を表す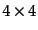 行列
行列
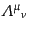 で表すこ
とができ、この行列が群をなしているが、これはローレンツ変換そのものが群
をなしていることのあらわれであって、なにもこの行列だけがローレンツ変換
を表すわけではない。ローレンツ群をこの
で表すこ
とができ、この行列が群をなしているが、これはローレンツ変換そのものが群
をなしていることのあらわれであって、なにもこの行列だけがローレンツ変換
を表すわけではない。ローレンツ群をこの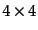 行列で表したように、
群を具体的な行列を使って表すことを、群の表現 (representation) と
いう。群の表現は一通りではなく、いくつも存在する。さらに、群の特定の表
現が作用する空間を表現空間 (representation space)という。上のロー
レンツ
行列で表したように、
群を具体的な行列を使って表すことを、群の表現 (representation) と
いう。群の表現は一通りではなく、いくつも存在する。さらに、群の特定の表
現が作用する空間を表現空間 (representation space)という。上のロー
レンツ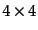 行列表現の場合、表現空間はベクトル空間
行列表現の場合、表現空間はベクトル空間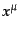 である。
である。
群に対する表現があったとき、ある表現空間の要素と、同じあるいは別の表現
空間の要素からテンソル積(tensor product)が定義できる。これはさら
に別の表現の表現空間になり、これに作用するあらたな表現は直積表現
(direct product representation) と呼ばれる。例として、ローレンツ群の
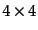 行列表現の中から、表現空間の要素であるベクトル
行列表現の中から、表現空間の要素であるベクトル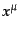 の単
なる積
の単
なる積
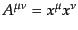 をひとつのテンソル積と定義すると、これ
は
をひとつのテンソル積と定義すると、これ
は
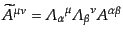 と変換する。ここで可能な添字
と変換する。ここで可能な添字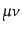 の組を適当に並べ替
えれば、この係数である
の組を適当に並べ替
えれば、この係数である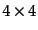 行列の要素の積は一つの行列要素と考え
ることができる。こうして作られる新しい行列による表現は直積表現の例となっ
ている。
行列の要素の積は一つの行列要素と考え
ることができる。こうして作られる新しい行列による表現は直積表現の例となっ
ている。
ある表現があり、その表現空間を線形変換することによってすべての表現行列
をブロック対角形にできる場合、そのブロック行列がひとつの表現となってい
て、表現が重複している。このとき、もとの表現は可約表現 (reducible
representation)と呼ばれる。可約表現でない表現を既約表現
(irreducible representation)と呼ぶ。既約表現においてはどの表現行列と
も可換になる行列は単位行列のみであることが知られている(シューアの補題)。
さて、ここで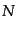 個の場
個の場
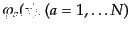 を考える。異なる
座標間で場の値は線形関係にあるはずだから、ローレンツ変換
を考える。異なる
座標間で場の値は線形関係にあるはずだから、ローレンツ変換
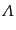 の
もとでは
の
もとでは
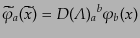 |
(H.3.59) |
と変換する。ここで、
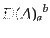 はローレンツ変換
はローレンツ変換
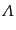 ごと
に決まる
ごと
に決まる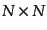 次の場の変換行列である。この式から、2つのローレン
ツ変換
次の場の変換行列である。この式から、2つのローレン
ツ変換
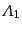 ,
,
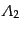 を連続して行ったときの場の変換行列は各
ローレンツ変換の場の変換行列の積
を連続して行ったときの場の変換行列は各
ローレンツ変換の場の変換行列の積
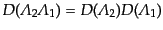 となることがわかる。これは変換行列
となることがわかる。これは変換行列
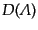 がローレンツ群のひとつの表現となっていることを意味する。
そして、場はその表現の表現空間である。こうして、相対論的に許される場を
見いだすことは、本義ローレンツ群の表現を見いだすことに等しいことがわか
る。
がローレンツ群のひとつの表現となっていることを意味する。
そして、場はその表現の表現空間である。こうして、相対論的に許される場を
見いだすことは、本義ローレンツ群の表現を見いだすことに等しいことがわか
る。
そこで、本義ローレンツ群の表現を求めるため、単位元近傍の無限小ローレン
ツ変換を考える。この場合、式(8.1.29)から、
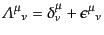 |
(H.3.60) |
である。ここで、無限小反対称テンソル
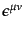 から作られる
から作られる
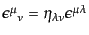 が無限小
パラメータとなっていて、変換のパラメータ数は6である。この変換の表現は
単位行列から無限小パラメータに比例する変化をするので、一般に、
が無限小
パラメータとなっていて、変換のパラメータ数は6である。この変換の表現は
単位行列から無限小パラメータに比例する変化をするので、一般に、
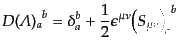 |
(H.3.61) |
と表される。ここで、
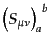 は添字
は添字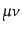 につ
いて反対称である。この量の添字
につ
いて反対称である。この量の添字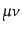 を固定したものを
を固定したものを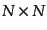 行列
行列
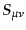 とみれば、
とみれば、
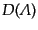 がローレンツ群の表現であるという条
件から、次の交換関係が導かれる:
がローレンツ群の表現であるという条
件から、次の交換関係が導かれる:
![$\displaystyle \left[S_{\mu\nu}, S_{\rho\sigma}\right] = \eta_{\nu\rho} S_{\mu\s...
...ho} S_{\nu\sigma} + \eta_{\nu\sigma} S_{\mu\rho} - \eta_{\mu\sigma} S_{\nu\rho}$](img1521.png) |
(H.3.62) |
この交換関係は具体的な表現によらない。また、この交換関係は逆にローレン
ツ群の積の構造を規定する。そこで、行列
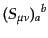 を表現行列の
一つとするような、抽象的な演算子
を表現行列の
一つとするような、抽象的な演算子
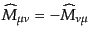 を
考える。これは、式(8.3.62)と同様の交換関係を満たす演算子である:
を
考える。これは、式(8.3.62)と同様の交換関係を満たす演算子である:
![$\displaystyle \left[\widehat{M}_{\mu\nu}, \widehat{M}_{\rho\sigma}\right] = \et...
...\eta_{\nu\sigma} \widehat{M}_{\mu\rho} - \eta_{\mu\sigma} \widehat{M}_{\nu\rho}$](img1524.png) |
(H.3.63) |
これはローレンツ群に対応するリー代数 (Lie algebra)の生成子
(generator)と呼ばれるものである。いま具体的な表現から離れ、交換関係
(8.3.62)をみたす生成子の既約表現を見つければ、ローレンツ群の既
約表現を見つけたことになる。
そこで、空間の添字を持つ次の演算子
| |
|
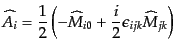 |
(H.3.64) |
| |
|
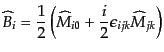 |
(H.3.65) |
を定義する。逆変換は
| |
|
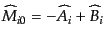 |
(H.3.66) |
| |
|
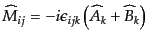 |
(H.3.67) |
である。すると、交換関係(8.3.63)は
| |
|
![$\displaystyle \left[\widehat{A}_i, \widehat{A}_j\right] = i \epsilon_{ijk} \widehat{A}_k$](img1529.png) |
(H.3.68) |
| |
|
![$\displaystyle \left[\widehat{B}_i, \widehat{B}_j\right] = i \epsilon_{ijk} \widehat{B}_k$](img1530.png) |
(H.3.69) |
| |
|
![$\displaystyle \left[\widehat{A}_i, \widehat{B}_j\right] = 0$](img1531.png) |
(H.3.70) |
と簡単化する。すなわち、
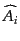 と
と
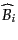 はお互いに可換で、それ
ぞれの交換関係は量子力学で見慣れた角運動量の交換関係となっている。つま
り、2つの独立な角運動量演算子の表現を求める問題に帰着する。したがって、
角運動量の理論から、
はお互いに可換で、それ
ぞれの交換関係は量子力学で見慣れた角運動量の交換関係となっている。つま
り、2つの独立な角運動量演算子の表現を求める問題に帰着する。したがって、
角運動量の理論から、
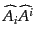 ,
,
 の固有
値をそれぞれ
の固有
値をそれぞれ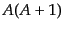 ,
, 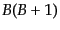 とするとき、
とするとき、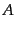 ,
, 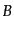 はゼロまたは正の整数
か半整数となる。これらの
はゼロまたは正の整数
か半整数となる。これらの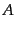 ,
, 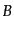 で特徴づけられる固有状態はそれぞれ
で特徴づけられる固有状態はそれぞれ
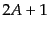 ,
, 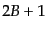 次元既約表現の表現空間の基底となり、それぞれ
次元既約表現の表現空間の基底となり、それぞれ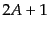 ,
,
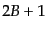 次元表現を構成する。
次元表現を構成する。
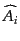 ,
,
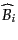 は独立な生成子であっ
て、一般の既約表現はこれらの直積表現により与えられる。その結果、ローレ
ンツ群の
は独立な生成子であっ
て、一般の既約表現はこれらの直積表現により与えられる。その結果、ローレ
ンツ群の
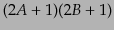 次元表現が構成され、ローレンツ群の表現が尽くさ
れることになる。これをローレンツ群の
次元表現が構成され、ローレンツ群の表現が尽くさ
れることになる。これをローレンツ群の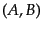 表現と呼ぶことにしよう。
表現と呼ぶことにしよう。
はじめに最も簡単な、ローレンツ群の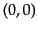 表現を考える。これは1次元表現
であるが、1次元行列では交換関係を表現できないのでリー代数の生成子の表
現はゼロ、
表現を考える。これは1次元表現
であるが、1次元行列では交換関係を表現できないのでリー代数の生成子の表
現はゼロ、
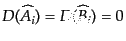 、つまり、群の表現行列がすべ
て1となる自明な表現である。したがって、この表現に対応する場
、つまり、群の表現行列がすべ
て1となる自明な表現である。したがって、この表現に対応する場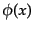 のローレンツ変換は
のローレンツ変換は
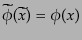 |
(H.3.71) |
すなわちスカラー関数であることがわかる。このような場をス
カラー場 (scalar field)という。
つぎに、ローレンツ群の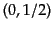 表現を考える。このとき、生成子
表現を考える。このとき、生成子
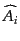 の表現は上と同様、自明な表現である。生成子
の表現は上と同様、自明な表現である。生成子
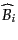 は角運
動量の2次元表現となり、パウリ行列
は角運
動量の2次元表現となり、パウリ行列
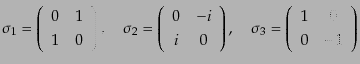 |
|
|
(H.3.72) |
を使って
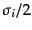 で表される。ここで、パウリ行列の性質を思い出してお
こう:
で表される。ここで、パウリ行列の性質を思い出してお
こう:
| |
|
![$\displaystyle [\sigma_i, \sigma_j]_+ =
\sigma_i\sigma_j + \sigma_j\sigma_i =
2 \delta_{ij} I$](img1549.png) |
(H.3.73) |
| |
|
![$\displaystyle [\sigma_i, \sigma_j] =
\sigma_i\sigma_j - \sigma_j\sigma_i =
2 i \epsilon_{ijk} \sigma_k$](img1550.png) |
(H.3.74) |
| |
|
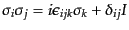 |
(H.3.75) |
すると、結局2次元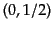 直積表現は、
直積表現は、
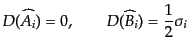 |
(H.3.76) |
となる。ここで、ローレンツ群のパラメータ
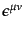 を式
(8.1.30) のように空間回転ベクトル
を式
(8.1.30) のように空間回転ベクトル
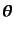 とローレンツ
ブーストベクトル
とローレンツ
ブーストベクトル
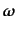 で書き直すと、ローレンツ群の表現行列
(8.3.61)は、
で書き直すと、ローレンツ群の表現行列
(8.3.61)は、
 |
(H.3.77) |
となる。これを有限変換に直した2次元表現を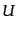 とすると、
とすると、
![$\displaystyle U({\mit\Lambda}) = \exp\left[ \frac{1}{2}\left(i{\mbox{\boldmath$...
...ta$}} -{\mbox{\boldmath$\omega$}}\right)\cdot{\mbox{\boldmath$\sigma$}} \right]$](img1556.png) |
(H.3.78) |
となる。パウリ行列はトレースなしであるから、6個の実数パラメータ
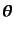 ,
,
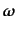 を動かすとき、この表現行列は
を動かすとき、この表現行列は
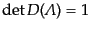 を満たす複素数上の
を満たす複素数上の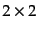 行列全体、すなわち
行列全体、すなわち
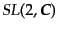 全体を覆っていることがわかる。この表現(8.3.78)
は
全体を覆っていることがわかる。この表現(8.3.78)
は
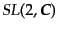 群のスピノル表現 (spinor representation)と呼ば
れる。この表現の表現空間は複素2次元空間の要素
群のスピノル表現 (spinor representation)と呼ば
れる。この表現の表現空間は複素2次元空間の要素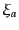 であり、
であり、
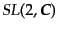 群の
群の
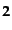 スピノルと呼ばれる。つまり、ローレンツ群の
スピノルと呼ばれる。つまり、ローレンツ群の
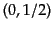 表現は
表現は
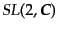 群のスピノル表現であったわけである。した
がって、
群のスピノル表現であったわけである。した
がって、
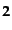 スピノルがいまの表現に対応する場
スピノルがいまの表現に対応する場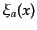 となってい
て、その変換は
となってい
て、その変換は
 |
(H.3.79) |
である。
ただし、ローレンツ群の元と
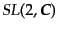 群の元は一対一対応ではない。
事実、空間をある方向に
群の元は一対一対応ではない。
事実、空間をある方向に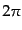 回転させる操作は、ローレンツ群では何もしな
い単位元に等価だが、
回転させる操作は、ローレンツ群では何もしな
い単位元に等価だが、
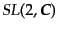 群の元(8.3.78)は、性質
(8.3.75)により、符合を変えることがわかる。単位元にまで戻すに
は
群の元(8.3.78)は、性質
(8.3.75)により、符合を変えることがわかる。単位元にまで戻すに
は 回転しなければならない。したがって、スピノル表現はローレンツ群
の2価表現となっている。
回転しなければならない。したがって、スピノル表現はローレンツ群
の2価表現となっている。
つぎに、ローレンツ群の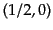 表現を考えるが、これは
表現を考えるが、これは
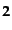 スピノル
表現から構成できるので、これを以下に説明する。そのため、まず
スピノル
表現から構成できるので、これを以下に説明する。そのため、まず
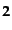 スピノル
スピノル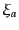 の複素共役
の複素共役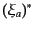 と同じ変換をする量
と同じ変換をする量
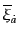 を考えてこれを
を考えてこれを
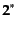 スピノルと呼ぶ。点つきの
添字によって
スピノルと呼ぶ。点つきの
添字によって
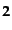 スピノルの添字と区別する。この
スピノルの添字と区別する。この
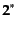 スピノル
の変換は、
スピノル
の変換は、
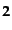 スピノルの変換からすぐわかるように、
スピノルの変換からすぐわかるように、
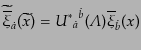 |
(H.3.80) |
である。ここで、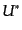 は
は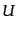 の複素共役行列である。
の複素共役行列である。
さて、スピノルの添字の上下を定義するため、
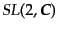 の不変テンソ
ルである2階反対称テンソル
の不変テンソ
ルである2階反対称テンソル
| |
|
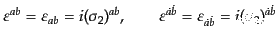 |
(H.3.81) |
| |
|
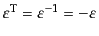 |
(H.3.82) |
を用いることにより、
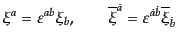 |
(H.3.83) |
とする。ここで、
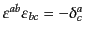 であるから、
添字を下げる時には
であるから、
添字を下げる時には
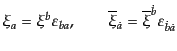 |
(H.3.84) |
とする。これは添字の縮約をするときには必ず左上と右下につながった対に限っ
て行う必要があることを意味する。他の縮約ではマイナスが付いたり付かなかっ
たりすることを忘れてはならない。すると、2つのスピノル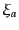 ,
,
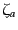 のスカラー積が
のスカラー積が
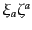 のように定義できる。これが変換で
確かに値を変えないことは、
のように定義できる。これが変換で
確かに値を変えないことは、
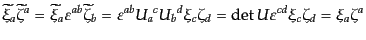 |
(H.3.85) |
によりわかる。ここで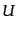 は
は
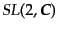 の元だから行列式が1であること
を使った。
の元だから行列式が1であること
を使った。
添字を上げた
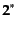 スピノル
スピノル
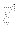 の変換は、
の変換は、
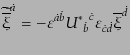 |
(H.3.86) |
となる。この変換の行列は
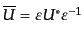 と表され
るが、直接確かめられる
と表され
るが、直接確かめられる
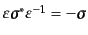 という関係を使えば、式(8.3.78)から、
という関係を使えば、式(8.3.78)から、
![$\displaystyle \overline{U}({\mit\Lambda}) = \exp\left[ \frac{1}{2}\left(i{\mbox...
...a$}} + {\mbox{\boldmath$\omega$}}\right)\cdot{\mbox{\boldmath$\sigma$}} \right]$](img1584.png) |
(H.3.87) |
であることがわかる。式(8.3.78)を導いたのと同様にして、
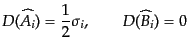 |
(H.3.88) |
の表現は
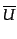 であることがわかるので、結局これはローレンツ群の
であることがわかるので、結局これはローレンツ群の
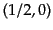 表現になっていることがわかる。
表現になっていることがわかる。
次に、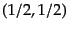 表現を考えよう。これは4次元表現であるが、下に見るよう
にその表現空間はよく知っているベクトル空間に等価なものになる。この
表現を考えよう。これは4次元表現であるが、下に見るよう
にその表現空間はよく知っているベクトル空間に等価なものになる。この
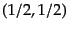 表現は
表現は
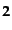 スピノル表現と
スピノル表現と
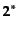 スピノル表現の直積
表現であるから、点なしと点つきの混合スピノル
スピノル表現の直積
表現であるから、点なしと点つきの混合スピノル
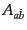 が表現空
間であり、その変換は
が表現空
間であり、その変換は
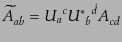 |
(H.3.89) |
である。この混合スピノルがベクトル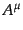 と一対一対応するのである。こ
れを示すため、
と一対一対応するのである。こ
れを示すため、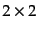 単位行列を
単位行列を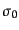 と書いてパウリ行列に加え、
4次元化したパウリ行列
と書いてパウリ行列に加え、
4次元化したパウリ行列
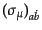 を考える。ここで、このス
ピノルの添字の位置をとるときにその行列要素が単位行列あるいは3つのパウ
リ行列となるように定義してある。また、空間方向にマイナスをつけたものを
を考える。ここで、このス
ピノルの添字の位置をとるときにその行列要素が単位行列あるいは3つのパウ
リ行列となるように定義してある。また、空間方向にマイナスをつけたものを
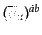 と定義する。すなわち、行列要素の関係と
して、
と定義する。すなわち、行列要素の関係と
して、
 |
(H.3.90) |
と定義したことになる。空間の添字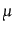 は計量テンソル
は計量テンソル
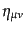 で上
げ下げできるものとする。また、スピノルの添字をあらわに示さないときはこ
の定義に示した標準位置にあるものとする。これらの量には次の関係がある:
で上
げ下げできるものとする。また、スピノルの添字をあらわに示さないときはこ
の定義に示した標準位置にあるものとする。これらの量には次の関係がある:
| |
|
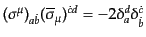 |
(H.3.91) |
| |
|
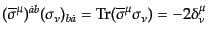 |
(H.3.92) |
| |
|
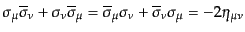 |
(H.3.93) |
さて、ベクトル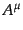 を表現空間とする表現の無限小変換は
を表現空間とする表現の無限小変換は
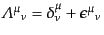 であるが、こ
れを式(8.3.61)と比べれば、その生成子は
であるが、こ
れを式(8.3.61)と比べれば、その生成子は
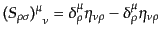 |
(H.3.94) |
であり、有限ローレンツ変換の変換行列は
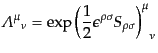 |
(H.3.95) |
となる。これと(8.3.78)により、
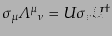 |
(H.3.96) |
であることが確かめられる。この関係を用いると、
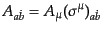 |
(H.3.97) |
が混合スピノルの変換をすることが容易に確かめられる。また、式
(8.3.92)を使うと、
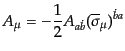 |
(H.3.98) |
となるので、結局混合スピノル
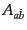 はベクトル
はベクトル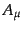 と一対一対
応にあることが確かめられたことになる。
と一対一対
応にあることが確かめられたことになる。
同様に考えていけば他の表現によってより複雑な表現を調べることができ、す
べての場はベクトルとスピノルを組み合わせた添字で表される変換をする場で
あることがわかる。詳細は省略するが、例えば、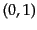 または
または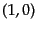 表現は
(反)自己双対2階反対称テンソル
表現は
(反)自己双対2階反対称テンソル
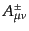 に等価であり、
に等価であり、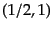 または
または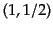 表現はベクトルとスピノルの添字をひとつずつ持ち、スピン
3/2の粒子を表す、ラリタ・シュウィンガー場 (Rarita-Schwinger field)
表現はベクトルとスピノルの添字をひとつずつ持ち、スピン
3/2の粒子を表す、ラリタ・シュウィンガー場 (Rarita-Schwinger field)
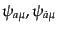 というものになる。
というものになる。





次へ: 古典的自由場
上へ: 場の量子化と粒子の相互作用
前へ: 場の理論の正準形式
目次
索引
All rights reserved © T.Matsubara 2004-2010
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11
![]() であるとする。
であるとする。
![]() 、つまり、何もしない変換に
連結な成分は順時間的固有ローレンツ変換である。これは、本義ローレ
ンツ変換とも呼ばれる。その他の非連結な成分は、時間反転、および空間反
転によって移り変わることができる。事実、時間反転は順時間的変換を逆時間
的にし、また、空間反転は固有ローレンツ変換を非固有ローレンツ変換にする
ことが明らかである。特殊相対論の要請を満たすには、本義ローレンツ変換の
もとで理論が不変であればよく、時間反転や空間反転の不変性については必ず
しも成り立ってなくてもよい。
、つまり、何もしない変換に
連結な成分は順時間的固有ローレンツ変換である。これは、本義ローレ
ンツ変換とも呼ばれる。その他の非連結な成分は、時間反転、および空間反
転によって移り変わることができる。事実、時間反転は順時間的変換を逆時間
的にし、また、空間反転は固有ローレンツ変換を非固有ローレンツ変換にする
ことが明らかである。特殊相対論の要請を満たすには、本義ローレンツ変換の
もとで理論が不変であればよく、時間反転や空間反転の不変性については必ず
しも成り立ってなくてもよい。
![]() 行列
行列
![]() で表すこ
とができ、この行列が群をなしているが、これはローレンツ変換そのものが群
をなしていることのあらわれであって、なにもこの行列だけがローレンツ変換
を表すわけではない。ローレンツ群をこの
で表すこ
とができ、この行列が群をなしているが、これはローレンツ変換そのものが群
をなしていることのあらわれであって、なにもこの行列だけがローレンツ変換
を表すわけではない。ローレンツ群をこの![]() 行列で表したように、
群を具体的な行列を使って表すことを、群の表現 (representation) と
いう。群の表現は一通りではなく、いくつも存在する。さらに、群の特定の表
現が作用する空間を表現空間 (representation space)という。上のロー
レンツ
行列で表したように、
群を具体的な行列を使って表すことを、群の表現 (representation) と
いう。群の表現は一通りではなく、いくつも存在する。さらに、群の特定の表
現が作用する空間を表現空間 (representation space)という。上のロー
レンツ![]() 行列表現の場合、表現空間はベクトル空間
行列表現の場合、表現空間はベクトル空間![]() である。
である。
![]() 行列表現の中から、表現空間の要素であるベクトル
行列表現の中から、表現空間の要素であるベクトル![]() の単
なる積
の単
なる積
![]() をひとつのテンソル積と定義すると、これ
は
をひとつのテンソル積と定義すると、これ
は
![]() と変換する。ここで可能な添字
と変換する。ここで可能な添字![]() の組を適当に並べ替
えれば、この係数である
の組を適当に並べ替
えれば、この係数である![]() 行列の要素の積は一つの行列要素と考え
ることができる。こうして作られる新しい行列による表現は直積表現の例となっ
ている。
行列の要素の積は一つの行列要素と考え
ることができる。こうして作られる新しい行列による表現は直積表現の例となっ
ている。
![]() 個の場
個の場
![]() を考える。異なる
座標間で場の値は線形関係にあるはずだから、ローレンツ変換
を考える。異なる
座標間で場の値は線形関係にあるはずだから、ローレンツ変換
![]() の
もとでは
の
もとでは
![]() 表現を考える。これは1次元表現
であるが、1次元行列では交換関係を表現できないのでリー代数の生成子の表
現はゼロ、
表現を考える。これは1次元表現
であるが、1次元行列では交換関係を表現できないのでリー代数の生成子の表
現はゼロ、
![]() 、つまり、群の表現行列がすべ
て1となる自明な表現である。したがって、この表現に対応する場
、つまり、群の表現行列がすべ
て1となる自明な表現である。したがって、この表現に対応する場![]() のローレンツ変換は
のローレンツ変換は
![]() 表現を考える。このとき、生成子
表現を考える。このとき、生成子
![]() の表現は上と同様、自明な表現である。生成子
の表現は上と同様、自明な表現である。生成子
![]() は角運
動量の2次元表現となり、パウリ行列
は角運
動量の2次元表現となり、パウリ行列
![]() 群の元は一対一対応ではない。
事実、空間をある方向に
群の元は一対一対応ではない。
事実、空間をある方向に![]() 回転させる操作は、ローレンツ群では何もしな
い単位元に等価だが、
回転させる操作は、ローレンツ群では何もしな
い単位元に等価だが、
![]() 群の元(8.3.78)は、性質
(8.3.75)により、符合を変えることがわかる。単位元にまで戻すに
は
群の元(8.3.78)は、性質
(8.3.75)により、符合を変えることがわかる。単位元にまで戻すに
は![]() 回転しなければならない。したがって、スピノル表現はローレンツ群
の2価表現となっている。
回転しなければならない。したがって、スピノル表現はローレンツ群
の2価表現となっている。
![]() 表現を考えるが、これは
表現を考えるが、これは
![]() スピノル
表現から構成できるので、これを以下に説明する。そのため、まず
スピノル
表現から構成できるので、これを以下に説明する。そのため、まず
![]() スピノル
スピノル![]() の複素共役
の複素共役![]() と同じ変換をする量
と同じ変換をする量
![]() を考えてこれを
を考えてこれを
![]() スピノルと呼ぶ。点つきの
添字によって
スピノルと呼ぶ。点つきの
添字によって
![]() スピノルの添字と区別する。この
スピノルの添字と区別する。この
![]() スピノル
の変換は、
スピノル
の変換は、
![]() スピノルの変換からすぐわかるように、
スピノルの変換からすぐわかるように、
![]() の不変テンソ
ルである2階反対称テンソル
の不変テンソ
ルである2階反対称テンソル
![]() スピノル
スピノル
![]() の変換は、
の変換は、
![]() 表現を考えよう。これは4次元表現であるが、下に見るよう
にその表現空間はよく知っているベクトル空間に等価なものになる。この
表現を考えよう。これは4次元表現であるが、下に見るよう
にその表現空間はよく知っているベクトル空間に等価なものになる。この
![]() 表現は
表現は
![]() スピノル表現と
スピノル表現と
![]() スピノル表現の直積
表現であるから、点なしと点つきの混合スピノル
スピノル表現の直積
表現であるから、点なしと点つきの混合スピノル
![]() が表現空
間であり、その変換は
が表現空
間であり、その変換は
![]() を表現空間とする表現の無限小変換は
を表現空間とする表現の無限小変換は
![]() であるが、こ
れを式(8.3.61)と比べれば、その生成子は
であるが、こ
れを式(8.3.61)と比べれば、その生成子は
![]() または
または![]() 表現は
(反)自己双対2階反対称テンソル
表現は
(反)自己双対2階反対称テンソル
![]() に等価であり、
に等価であり、![]() または
または![]() 表現はベクトルとスピノルの添字をひとつずつ持ち、スピン
3/2の粒子を表す、ラリタ・シュウィンガー場 (Rarita-Schwinger field)
表現はベクトルとスピノルの添字をひとつずつ持ち、スピン
3/2の粒子を表す、ラリタ・シュウィンガー場 (Rarita-Schwinger field)
![]() というものになる。
というものになる。
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11