




次へ: 相対論的に可能な場
上へ: 場の量子化と粒子の相互作用
前へ: 作用の原理
目次
索引
Subsections
ここまでラグランジアン形式で考えてきたが、これを正準形式へ移行すること
を考えよう。通常の有限自由度の力学系における正準形式への移行を連続場の
場合に拡張すればよい。まず、場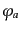 の共役運動量を
の共役運動量を
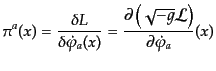 |
(H.2.38) |
で導入する。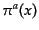 および
および
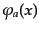 を合わせて正準変数と呼ぶ。こ
の式から
を合わせて正準変数と呼ぶ。こ
の式から
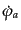 を
を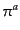 ,
, 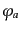 , および
, および
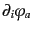 の関数として表し、ハミルトニアンを構成する:
の関数として表し、ハミルトニアンを構成する:
![$\displaystyle H = \int d^3x \pi^a(x) \dot{\varphi}_a \left[\pi^a(x), \varphi_a(x), \partial_i\varphi_a(x)\right] - L$](img1458.png) |
(H.2.39) |
これは、正準変数の汎関数となっている。ここで、ハミルトニアン密度
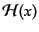 を
を
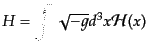 |
(H.2.40) |
で定義すると、
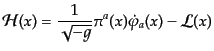 |
(H.2.41) |
である。ここで、左辺では式(8.2.38)を使って
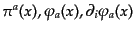 の関数として表してあるものとする。
このことに注意すると、オイラー・ラグランジュの方程式(8.1.8)と
式(8.2.39)により、正準方程式
の関数として表してあるものとする。
このことに注意すると、オイラー・ラグランジュの方程式(8.1.8)と
式(8.2.39)により、正準方程式
が導かれる。
これら、正準方程式により、一般に正準変数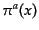 ,
,
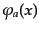 の任
意汎関数
の任
意汎関数
![$ F[\pi, \varphi]$](img1467.png) の時間微分は、
の時間微分は、
![$\displaystyle \frac{d}{dt}F[\pi, \varphi] = \int d^3x \left[ \frac{\delta F}{\d...
...ldmath$x$}})} \frac{\delta H}{\delta\varphi_a(t,{\mbox{\boldmath$x$}})} \right]$](img1468.png) |
(H.2.44) |
となる。ここで、正準変数の任意汎関数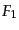 ,
, 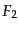 についてのポアソン括
弧を次式で定義する:
についてのポアソン括
弧を次式で定義する:
![$\displaystyle \left\{F_1, F_2\right\}_{\rm P} = \int d^3x \left[ \frac{\delta F...
...}{\delta\varphi_a(t,{\mbox{\boldmath$x$}})} \right] = - \left\{F_2, F_1\right\}$](img1471.png) |
(H.2.45) |
すると容易に、
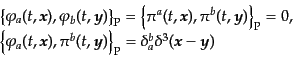 |
(H.2.46) |
が導かれる。また、正準方程式(8.2.42), (8.2.43)は
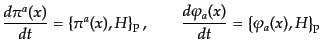 |
(H.2.47) |
と表すことができる。同様に、式(8.2.44)は
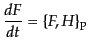 |
(H.2.48) |
となる。
正準エネルギー運動量テンソルからつくられる保存量 は
は
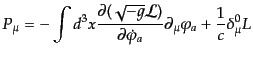 |
(H.2.49) |
である。これを正準変数で書き表したとき、その時間成分は式
(8.2.39)で与えられるハミルトニアンと
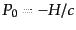 の関係にある
ことがわかる。すると、式(8.2.48)を場の量
の関係にある
ことがわかる。すると、式(8.2.48)を場の量
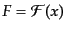 につい
て適用した式は、
につい
て適用した式は、
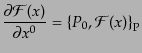 |
(H.2.50) |
とかくことができる。理論が相対論的に不変であるならば、この式の一般化で
ある
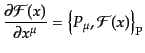 |
(H.2.51) |
が成り立つはずである。実際、式(8.2.49)の空間成分
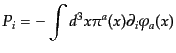 |
(H.2.52) |
により、ポアソン括弧を直接計算すれば、式(8.2.51)の空間成分を示
すことができる。この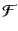 として正準変数そのものをとると、
として正準変数そのものをとると、
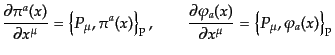 |
(H.2.53) |
となる。これが相対論的に一般化された正準方程式である。





次へ: 相対論的に可能な場
上へ: 場の量子化と粒子の相互作用
前へ: 作用の原理
目次
索引
All rights reserved © T.Matsubara 2004-2010
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11
![]() の共役運動量を
の共役運動量を
![]() ,
,
![]() の任
意汎関数
の任
意汎関数
![]() の時間微分は、
の時間微分は、
![]() は
は
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11