




次へ: 場の理論の正準形式
上へ: 場の量子化と粒子の相互作用
前へ: 場の量子化と粒子の相互作用
目次
索引
Subsections
物理学において、系の基本的な物理的性質は作用(action)
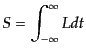 |
(H.1.1) |
によって決定される。ここで, はラグランジアンである.物理系を記述す
る方程式は運動方程式と呼ばれ,作用を最小にするような時間発展をするもの
である.したがって,運動方程式は,系の時間発展の経路について微小変化さ
せたとき,
はラグランジアンである.物理系を記述す
る方程式は運動方程式と呼ばれ,作用を最小にするような時間発展をするもの
である.したがって,運動方程式は,系の時間発展の経路について微小変化さ
せたとき,
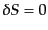 となる条件を課すことにより得ることができる.こ
れを最小作用の原理という.
となる条件を課すことにより得ることができる.こ
れを最小作用の原理という.
場とは,空間のあらゆる点すべてに力学的自由度が割り当てられるようなもの
である.例えば電磁場においては,空間の各点に電場ベクトル,磁場ベクトル
があり、そのすべてが力学的自由度となる。このように、場の理論においては,
自由度が無限大である。場の相互作用が局所的である限り、ラグランジアンは
空間の各点における場のラグランジアンの和となり,
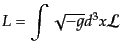 |
(H.1.2) |
と表される。この空間の各点のラグランジアン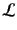 はラグランジア
ン密度(Lagrangian density)と呼ばれる.また因子
はラグランジア
ン密度(Lagrangian density)と呼ばれる.また因子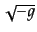 が空間積分
の重みとしてついているのは、すぐ下で明らかになるようにラグランジアン密
度をローレンツ不変にするためである。すると作用は次の形で表されることに
なる:
が空間積分
の重みとしてついているのは、すぐ下で明らかになるようにラグランジアン密
度をローレンツ不変にするためである。すると作用は次の形で表されることに
なる:
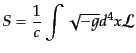 |
(H.1.3) |
ローレンツ不変性を満たす運動方程式を導くためには作用積分自体がローレン
ツ不変である必要がある。4次元体積素片
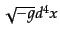 はローレンツ不変なので、
ラグランジアン密度はローレンツ不変な形になる。
はローレンツ不変なので、
ラグランジアン密度はローレンツ不変な形になる。
局所相互作用を持つ通常の物理系では,ラグランジアン密度は場
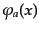 とその1階微分
とその1階微分
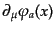 の関数
の関数
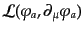 となる.ここで、
となる.ここで、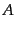 は複数の場が
共存するとき、それらの場を区別する添字である。
は複数の場が
共存するとき、それらの場を区別する添字である。
運動方程式を求めるため,各点における場の微小変化
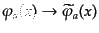 を考える.この微小変化
を考える.この微小変化
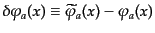 |
(H.1.4) |
によって作用が変化しないような場が運動方程式の解である.作用の変化は
![$\displaystyle c\delta S = \int d^4x \left[ \frac{\partial \left(\sqrt{-g}{\cal ...
...ght)} {\partial(\partial_\mu \varphi_a)} \delta(\partial_\mu \varphi_a) \right]$](img1389.png) |
(H.1.5) |
となる。ここで、場の種類を表す添字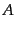 についても、繰り返し現れてきたと
きは和をとるという規約を用いている。すると、微分の変分は
についても、繰り返し現れてきたと
きは和をとるという規約を用いている。すると、微分の変分は
![$\displaystyle \delta \left[\partial_\mu \varphi_a (x)\right] = \partial_\mu \wi...
...hi}_a(x) - \varphi_a(x)\right] = \partial_\mu \left[\delta \varphi_a (x)\right]$](img1390.png) |
(H.1.6) |
と交換するので,式(8.1.5)で第2項を部分積分することにより,
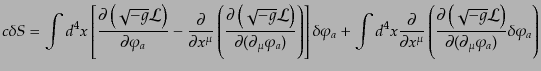 |
(H.1.7) |
が得られる.最後の項は境界項であり,無限大の彼方での変分をゼロとするよ
うな境界条件を課せば,消すことができる.したがって最小作用の原理
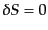 から,運動方程式は,
から,運動方程式は,
![$\displaystyle \frac{\partial \left({\sqrt{-g}}{\cal L}\right)}{\partial\varphi_...
...l\left(\sqrt{-g}{\cal L}\right)} {\partial(\partial_\mu \varphi_a)} \right] = 0$](img1392.png) |
(H.1.8) |
となる.これが場のオイラー・ラグランジュの方程式である.あるいは単に運
動方程式と呼ばれる.
系における保存量の存在はその系の対称性の現れである.解析力学でよく知ら
れているようにエネルギー保存則は時間並進の対称性,運動量保存則は空間並
進の対称性,角運動量保存則は回転の対称性,がそれぞれ対応している.これ
を一般化したものがネーターの定理である.一般に,系に連続的な対称性が存
在するとき,その系には対応する保存則が必ず存在する.
これを証明するため,ラグランジアン密度を不変に保つ変換があると仮定しよ
う。一般にこの変換のパラメータは複数個あり、それを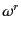 として、そ
の微小変換
として、そ
の微小変換
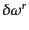 を考える.この変換のもとで、
を考える.この変換のもとで、
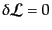 となる。一般のため,複数の場
となる。一般のため,複数の場
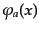 がその対称性に関わると
しておく.座標
がその対称性に関わると
しておく.座標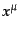 と場の値
と場の値
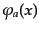 を同時に微小変換するときの
変換を
を同時に微小変換するときの
変換を
とおく.このとき,場を同一の座標点で比べた関数系の変化は
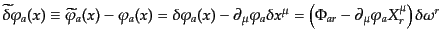 |
(H.1.11) |
となる。同様に、量
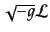 の変換を同一の座標点で比べた関数
系の変化で書き直すと、
の変換を同一の座標点で比べた関数
系の変化で書き直すと、
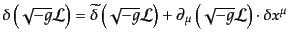 |
(H.1.12) |
となるが、第1項はオイラー・ラグランジュの方程式を使うことにより、
![$\displaystyle \widetilde{\delta}\left(\sqrt{-g}{\cal L}\right) = \frac{\partial...
...partial\left(\partial_\mu \varphi_a\right)} \widetilde{\delta}\varphi_a \right]$](img1403.png) |
(H.1.13) |
となることがわかる。また、計量の変換は
である。ここで、行列の微分の関係式、
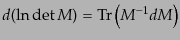 |
(H.1.15) |
によれば、
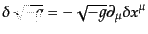 |
(H.1.16) |
であることがわかる。したがって、式(8.1.12), (8.1.13),
(8.1.16)により、
![$\displaystyle \sqrt{-g} \delta{\cal L} = \delta\left(\sqrt{-g}{\cal L}\right) -...
..._a\right)} \widetilde{\delta}\varphi_a + \sqrt{-g}{\cal L} \delta x^\mu \right]$](img1410.png) |
(H.1.17) |
となる。ここで、
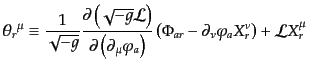 |
(H.1.18) |
とおくと、式(8.1.17)がゼロになる条件により、
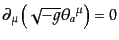 |
(H.1.19) |
という式が成り立つことになる。これが系の対称性から結論される保存則であ
り、
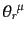 はネーターカレント(Noether current)と呼ばれ
る。このような発散ゼロのベクトルを保存カレントという。このとき,
はネーターカレント(Noether current)と呼ばれ
る。このような発散ゼロのベクトルを保存カレントという。このとき,
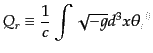 |
(H.1.20) |
が保存量となるH1。事実,
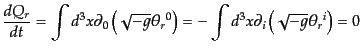 |
(H.1.21) |
となって時間的に一定値をとることがわかる.このような
保存則(8.1.19)を満たすようなカレントの取り方は一意的ではない。
それは、任意の反対称テンソル
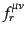 から、
から、
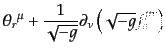 |
(H.1.22) |
をつくると、これも同様に保存則を満たすことになる。つまり、この分だけ保
存するネーターカレントに不定性がある。この不定性を用いれば、ネーターカ
レントにある種の望ましい性質を持つようにすることができる。
ラグランジアン密度を不変に保つ変換の特別な場合として、時空間に並進対称
性がある場合を考える。これは、時空の座標の並進
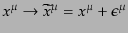 |
(H.1.23) |
について、系が対称であることを意味する。ここで、
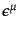 は
は
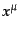 には無関係な無限小パラメータである。場の量については、これは座
標の付け変えにすぎないので、この変換のもとでは
には無関係な無限小パラメータである。場の量については、これは座
標の付け変えにすぎないので、この変換のもとでは
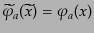 |
(H.1.24) |
である。すると、上の一般論で、
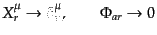 |
(H.1.25) |
としたものであるから、この場合のネーターカレントは、
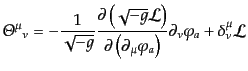 |
(H.1.26) |
である。これを、場の正準エネルギー運動量テンソル(canonical
energy-momentum tensor)という。
保存則(8.1.19)は
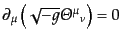 |
(H.1.27) |
となる。さらに保存量は
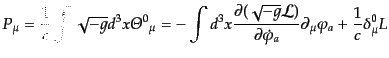 |
(H.1.28) |
である。ここで、ドットは時間微分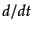 を表し、
を表し、 は全ラグランジアンで
ある。良く知られている系において具体的なラグランジアンを使ってこの保存
量を計算してみると、この保存量の時間成分
は全ラグランジアンで
ある。良く知られている系において具体的なラグランジアンを使ってこの保存
量を計算してみると、この保存量の時間成分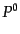 および空間成分
および空間成分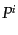 はそれ
ぞれ場の全エネルギーと全運動量に対応する、全4元運動量であることがわか
る。この導出において、時間が一様であればエネルギーが保存し、空間がある
方向に一様であればその方向の運動量が保存することが明らかである。
はそれ
ぞれ場の全エネルギーと全運動量に対応する、全4元運動量であることがわか
る。この導出において、時間が一様であればエネルギーが保存し、空間がある
方向に一様であればその方向の運動量が保存することが明らかである。
正準エネルギー運動量テンソルはは式(B.2.80)で表される物質のエネル
ギー運動量テンソル
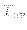 とは異なるので注意を要する。ラグランジア
ンによっては両者は一致することもあるが、必ずしも一般に一致するわけでは
ない。後者は一般に対称テンソルであるが、正準エネルギー運動量テンソルは
一般には対称テンソルとは限らない。だが、上で述べたネーターカレントの不
定性を用いれば、保存則(8.1.27)を満たしつつ、対称となるテンソル
を正準エネルギー運動量テンソルからつくることができる。
とは異なるので注意を要する。ラグランジア
ンによっては両者は一致することもあるが、必ずしも一般に一致するわけでは
ない。後者は一般に対称テンソルであるが、正準エネルギー運動量テンソルは
一般には対称テンソルとは限らない。だが、上で述べたネーターカレントの不
定性を用いれば、保存則(8.1.27)を満たしつつ、対称となるテンソル
を正準エネルギー運動量テンソルからつくることができる。
もう一つの例として、平坦な空間中での一様なローレンツ変換について系が対
称である場合を考える。このとき、計量は
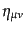 であり、座標の変
換は
であり、座標の変
換は
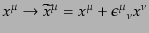 |
(H.1.29) |
で与えられる。ここで、
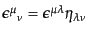 は6つの自由度を持つ無限小反対称行列
は6つの自由度を持つ無限小反対称行列
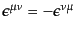 の添字を下げたものである。この変
換が確かにローレンツ変換であることは、式(B.1.4)が微小量
の添字を下げたものである。この変
換が確かにローレンツ変換であることは、式(B.1.4)が微小量
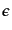 の一次までで成り立っていることからわかる。さらにまた、次の3
次元ベクトル
の一次までで成り立っていることからわかる。さらにまた、次の3
次元ベクトル
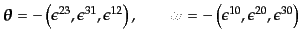 |
(H.1.30) |
はそれぞれ微小空間回転、微小ローレンツブーストを表す微小ベクトルとなっ
ている。この場合、場の無限小変換は一般に
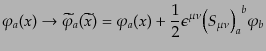 |
(H.1.31) |
と表される。この係数
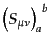 はローレンツ変換の
もとでの場の変換性を指定し、添字
はローレンツ変換の
もとでの場の変換性を指定し、添字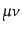 について反対称な量である。
について反対称な量である。
これらの変換は、上で与えたネーターの定理の一般論において変換の無限小パ
ラメータ
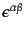 で、
で、
![$\displaystyle X_r^\mu \rightarrow \delta^\mu_{[\alpha} x_{\beta]}, \qquad \Phi_{ar} \rightarrow \frac12 {\left(S_{\alpha\beta}\right)_a}^b \varphi_b$](img1439.png) |
(H.1.32) |
と対応させたものである。ここで、![$ [\cdots]$](img1440.png) は中に含まれる添字に関して反
対称化することを表し、具体的には
は中に含まれる添字に関して反
対称化することを表し、具体的には
![$\displaystyle \delta^\mu_{[\alpha} x_{\beta]} = \frac12 \left(\delta^\mu_\alpha x_\beta - \delta^\mu_\beta x_\alpha\right)$](img1441.png) |
(H.1.33) |
である。するとネーターカレントは
![$\displaystyle \theta^\mu_{\alpha\beta} = \frac12\left[ \frac{\partial{\cal L}}{...
...a}_a}^\mu}_\beta x_\alpha \right] \equiv \frac{1}{2} {\cal M}^\mu_{\alpha\beta}$](img1442.png) |
(H.1.34) |
となる。ここで、
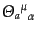 は場
は場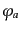 に対する、(平
坦時空の場合の)式(8.1.26)で与えられる正準エネルギー運動量テン
ソルである。この保存カレント
に対する、(平
坦時空の場合の)式(8.1.26)で与えられる正準エネルギー運動量テン
ソルである。この保存カレント
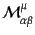 を4次元
角運動量テンソル密度といい、保存則は
を4次元
角運動量テンソル密度といい、保存則は
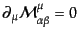 |
(H.1.35) |
で、保存量は
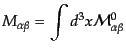 |
(H.1.36) |
である。
この保存量は3次元角運動量の拡張になっている。事実、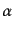 ,
, 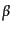 が空間成分
が空間成分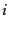 ,
, 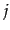 をとるとき、上の保存量は
をとるとき、上の保存量は
![$\displaystyle M_{ij} = \int d^3x \left[ \frac{\partial{\cal L}}{\partial(\parti...
...}^b \varphi_b + {{{\mit\Theta}_a}^0}_i x_j - {{{\mit\Theta}_a}^0}_j x_i \right]$](img1451.png) |
(H.1.37) |
となるが、
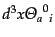 は体積要素中の運動量に対応するので、
上式の最後の2項は軌道角運動量に対応している。場の理論では、軌道角運動
量のみでは保存せず、場の非自明なローレンツ変換性による寄与である第1項
を加えてはじめて保存している。この項は場
は体積要素中の運動量に対応するので、
上式の最後の2項は軌道角運動量に対応している。場の理論では、軌道角運動
量のみでは保存せず、場の非自明なローレンツ変換性による寄与である第1項
を加えてはじめて保存している。この項は場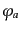 の持つスピン角
運動量 と呼ばれる。これら3つの空間的な角運動量に加えて、エネルギーと
時間によりつくられる一般化された角運動量があと3つ存在し、ローレンツ不
変な系の保存量となっている。
の持つスピン角
運動量 と呼ばれる。これら3つの空間的な角運動量に加えて、エネルギーと
時間によりつくられる一般化された角運動量があと3つ存在し、ローレンツ不
変な系の保存量となっている。
Footnotes
- ...
が保存量となるH1
- この定義は時間一定面の取り方に依存しているので、
ローレンツ不変でない定義となっていることに注意。





次へ: 場の理論の正準形式
上へ: 場の量子化と粒子の相互作用
前へ: 場の量子化と粒子の相互作用
目次
索引
All rights reserved © T.Matsubara 2004-2010
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11
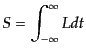
![]() とその1階微分
とその1階微分
![]() の関数
の関数
![]() となる.ここで、
となる.ここで、![]() は複数の場が
共存するとき、それらの場を区別する添字である。
は複数の場が
共存するとき、それらの場を区別する添字である。
![]() を考える.この微小変化
を考える.この微小変化
![]() として、そ
の微小変換
として、そ
の微小変換
![]() を考える.この変換のもとで、
を考える.この変換のもとで、
![]() となる。一般のため,複数の場
となる。一般のため,複数の場
![]() がその対称性に関わると
しておく.座標
がその対称性に関わると
しておく.座標![]() と場の値
と場の値
![]() を同時に微小変換するときの
変換を
を同時に微小変換するときの
変換を
![]() から、
から、
![]() とは異なるので注意を要する。ラグランジア
ンによっては両者は一致することもあるが、必ずしも一般に一致するわけでは
ない。後者は一般に対称テンソルであるが、正準エネルギー運動量テンソルは
一般には対称テンソルとは限らない。だが、上で述べたネーターカレントの不
定性を用いれば、保存則(8.1.27)を満たしつつ、対称となるテンソル
を正準エネルギー運動量テンソルからつくることができる。
とは異なるので注意を要する。ラグランジア
ンによっては両者は一致することもあるが、必ずしも一般に一致するわけでは
ない。後者は一般に対称テンソルであるが、正準エネルギー運動量テンソルは
一般には対称テンソルとは限らない。だが、上で述べたネーターカレントの不
定性を用いれば、保存則(8.1.27)を満たしつつ、対称となるテンソル
を正準エネルギー運動量テンソルからつくることができる。
![]() であり、座標の変
換は
であり、座標の変
換は
![]() で、
で、
![]() ,
, ![]() が空間成分
が空間成分![]() ,
, ![]() をとるとき、上の保存量は
をとるとき、上の保存量は
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11