




次へ: 原始ニュートリノ
上へ: ビッグバン宇宙モデル
前へ: 物質優勢と輻射優勢
目次
索引
宇宙の初期では温度が高く,粒子は頻繁に相互作用をすることによって強く結
合し,熱平衡状態となっている.粒子間にはエネルギー交換がおこり,また,
相対論的な粒子は生成消滅を頻繁に起こしたりしている.やがて宇宙の温度が
下がってくると,粒子間の相互作用は弱くなり,お互いのエネルギーのやりと
りがなくなって独立に運動するようになる.この過程を粒子の脱結合
(decoupling)という.宇宙の熱史の中でどのような粒子の間の相互作用がい
つ脱結合したのかは,宇宙の進化にとって本質的なことであり,大変重要なこ
とである.
脱結合の過程は非熱平衡状態であるので,これを正確に扱うには非平衡統計力
学を用いて調べることができる.だが,定性的なふるまいを知るだけであれば
もっと簡単な方法があるので,まずここではそれを見てみよう.ある粒子が単
位時間あたりに他の粒子と何らかの相互作用をする確率を
 とする.
すると脱結合をしているかどうかは,その粒子が相互作用するのに宇宙年齢の
オーダーの時間がかかるかどうかでおおざっぱに判定できると考えられる.宇
宙年齢のオーダーはその時点でのハッブルパラメータの逆数で表されるから,
判定条件として,
とする.
すると脱結合をしているかどうかは,その粒子が相互作用するのに宇宙年齢の
オーダーの時間がかかるかどうかでおおざっぱに判定できると考えられる.宇
宙年齢のオーダーはその時点でのハッブルパラメータの逆数で表されるから,
判定条件として,
 |
(D.3.33) |
という単純なものが考えられる.これは単純なわりには実際の正確な取扱いの
定性的な性質を大変よく説明し,有用なものとしてよく用いられるものである.
この条件はガモフの基準 (Gamov's criteria)と呼ばれる.
通常,宇宙の膨張に伴って温度と密度が下がることで,粒子の相互作用の確率
は時間とともに小さくなる.ハッブルパラメータの値も緩やかに減少していく
が,相互作用の確率の方が急速に小さくなるので,初期に他の粒子と結合して
いた粒子も,
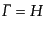 となる時点あたりで,脱結合することになる.
となる時点あたりで,脱結合することになる.
脱結合後の粒子は自由に膨張宇宙の重力場中を自由落下運動することになる.
脱結合の起こった後も,重力場を通じた相互作用は存在するが,言葉の問題と
して,通常重力相互作用によるものは結合とは呼ばないことが多い.膨張宇宙
における自由落下運動を調べるため,測地線方程式の0-成分を考える:
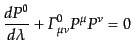 |
(D.3.34) |
ここで,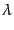 はアフィンパラメータであり,
はアフィンパラメータであり,
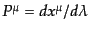 は
4元運動量である.このアフィンパラメータは粒子に質量があるときにはその
粒子の固有時を質量で割ったものである.RW計量のクリストッフェル記号
(3.1.5)により,測地線方程式は
は
4元運動量である.このアフィンパラメータは粒子に質量があるときにはその
粒子の固有時を質量で割ったものである.RW計量のクリストッフェル記号
(3.1.5)により,測地線方程式は
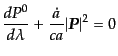 |
(D.3.35) |
となる.ここで,4元運動量の3次元成分の大きさとして,
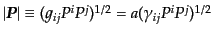 を用いている.
4元運動量の性質
を用いている.
4元運動量の性質
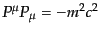 により,
により,
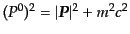 ,したがって,
,したがって,
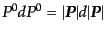 であること,ま
た,
であること,ま
た,
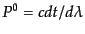 であることから,
であることから,
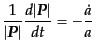 |
(D.3.36) |
が導かれ,これを積分すると
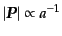 |
(D.3.37) |
となることがわかる.
脱結合した粒子はもはや熱平衡状態にないが,このように運動量は一様にスケー
ル因子に反比例して小さくなっていくだけのため,分布関数は比較的単純な形
をとり続ける.化学ポテンシャルの無視できる相対論的粒子の場合を考えてみ
よう.この場合,粒子のエネルギーは
 で与えられるので,エ
ネルギーそのものがスケール因子に反比例することになる.これは例えば光子
のエネルギーが振動数に比例することを思い出せば,波長の赤方偏移から導き
出されることでもある.この場合の分布関数の変化は次のようにわかる.まず,
脱結合時に位相体積中の位置
で与えられるので,エ
ネルギーそのものがスケール因子に反比例することになる.これは例えば光子
のエネルギーが振動数に比例することを思い出せば,波長の赤方偏移から導き
出されることでもある.この場合の分布関数の変化は次のようにわかる.まず,
脱結合時に位相体積中の位置
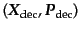 にあっ
た粒子が脱結合後の時刻
にあっ
た粒子が脱結合後の時刻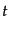 に位置
に位置
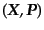 へ移動するとする.
このとき,粒子数が保存していることから両時刻における分布関数には
へ移動するとする.
このとき,粒子数が保存していることから両時刻における分布関数には
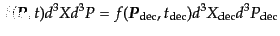 |
(D.3.38) |
の関係がある.いま,位相空間を考えているので
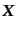 は共動座標ではな
く,物理的スケールを表す座標であることに注意すると,座標体積素片につい
て
は共動座標ではな
く,物理的スケールを表す座標であることに注意すると,座標体積素片につい
て
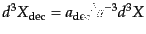 の関係がある.ここで,
の関係がある.ここで,
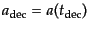 は脱結合時のスケール因子である.また,運動
量はスケール因子に反比例するので,
は脱結合時のスケール因子である.また,運動
量はスケール因子に反比例するので,
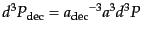 の関係がある.したがって,位相体積素片は不変であるが,これは
実はリュービルの定理と呼ばれる一般的に成り立つ事実である.したがって,
時刻
の関係がある.したがって,位相体積素片は不変であるが,これは
実はリュービルの定理と呼ばれる一般的に成り立つ事実である.したがって,
時刻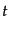 の分布関数は容易に求められ,
の分布関数は容易に求められ,
![$\displaystyle f({\mbox{\boldmath$P$}},t) = \left[ \exp \left( \frac{c\vert{\mbo...
...th$P$}}\vert}{k_{\rm B} a_{\rm dec}T_{\rm dec}/a(t)} \right) \pm 1 \right]^{-1}$](img547.png) |
(D.3.39) |
となる.ここで,
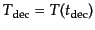 は脱結合時の温度である.こ
の最後の形をみると,分布関数は熱平衡の形を保ったまま,温度が
は脱結合時の温度である.こ
の最後の形をみると,分布関数は熱平衡の形を保ったまま,温度が
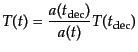 |
(D.3.40) |
となっていることがわかる.脱結合後は平衡ではないにもかかわらず,この意
味で温度という概念が存在する.この場合,宇宙の温度はスケール因子に反
比例していることがわかるが,このふるまいもほぼ平衡状態にあるときと同じ
である.ただ,平衡状態にあるときと違うのは,他の粒子とのエネルギーのや
りとりがないので,エントロピー流入によって温度の冷却が鈍るようなことは
なく,他の粒子とは独立に,ただ単純に膨張に反比例して冷却していくのみで
ある.
次に非相対論的粒子の場合を見てみよう.このときは粒子の4元運動量の3次元
成分は
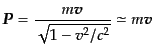 |
(D.3.41) |
となるため,3次元速度
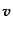 がスケール因子に反比例して減少することに
なる:
がスケール因子に反比例して減少することに
なる:
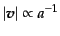 |
(D.3.42) |
非相対論的粒子はMaxwell-Boltzmann分布
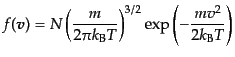 |
(D.3.43) |
に従う.ここで,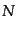 は単位体積あたりの数密度である.これについて上と同
様にすれば,
は単位体積あたりの数密度である.これについて上と同
様にすれば,
となる.したがって,やはり熱平衡の形を保ったまま,温度が
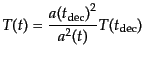 |
(D.3.45) |
となっている.相対論的粒子に比べるとさらに急速に温度が低下するため,脱
結合後の非相対論的粒子のこの意味での温度は相対論的粒子のものよりもずっ
と小さくなる.





次へ: 原始ニュートリノ
上へ: ビッグバン宇宙モデル
前へ: 物質優勢と輻射優勢
目次
索引
All rights reserved © T.Matsubara 2004-2010
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11
![]() とする.
すると脱結合をしているかどうかは,その粒子が相互作用するのに宇宙年齢の
オーダーの時間がかかるかどうかでおおざっぱに判定できると考えられる.宇
宙年齢のオーダーはその時点でのハッブルパラメータの逆数で表されるから,
判定条件として,
とする.
すると脱結合をしているかどうかは,その粒子が相互作用するのに宇宙年齢の
オーダーの時間がかかるかどうかでおおざっぱに判定できると考えられる.宇
宙年齢のオーダーはその時点でのハッブルパラメータの逆数で表されるから,
判定条件として,
![]() となる時点あたりで,脱結合することになる.
となる時点あたりで,脱結合することになる.
![]() で与えられるので,エ
ネルギーそのものがスケール因子に反比例することになる.これは例えば光子
のエネルギーが振動数に比例することを思い出せば,波長の赤方偏移から導き
出されることでもある.この場合の分布関数の変化は次のようにわかる.まず,
脱結合時に位相体積中の位置
で与えられるので,エ
ネルギーそのものがスケール因子に反比例することになる.これは例えば光子
のエネルギーが振動数に比例することを思い出せば,波長の赤方偏移から導き
出されることでもある.この場合の分布関数の変化は次のようにわかる.まず,
脱結合時に位相体積中の位置
![]() にあっ
た粒子が脱結合後の時刻
にあっ
た粒子が脱結合後の時刻![]() に位置
に位置
![]() へ移動するとする.
このとき,粒子数が保存していることから両時刻における分布関数には
へ移動するとする.
このとき,粒子数が保存していることから両時刻における分布関数には
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11