




次へ: ガモフの基準と脱結合
上へ: ビッグバン宇宙モデル
前へ: 初期宇宙の熱力学
目次
索引
上で見たように,輻射のエネルギー密度は
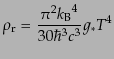 |
(D.2.21) |
となる.したがって,現在の値は,
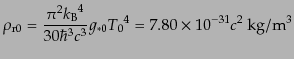 |
(D.2.22) |
である.ここで,最後の数値では,光子温度の現在値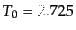 ,および,
現在の相対論的なニュートリノが3種類ある場合の有効自由度
,および,
現在の相対論的なニュートリノが3種類ある場合の有効自由度
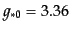 を使った.これは密度パラメータにすれば,
を使った.これは密度パラメータにすれば,
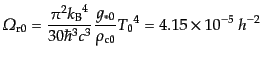 |
(D.2.23) |
となる.したがって,式(4.2.21)は
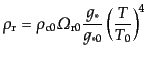 |
(D.2.24) |
とかける.
十分高温の平衡状態にある宇宙では,輻射成分が宇宙のエネルギー密度の大半
を担っているのだが,冷却してくると対消滅しないで残っている非相対論的物
質が宇宙のエネルギー密度において優勢になってくる.これがいつ起こるのか
を見るためには,物質のエネルギー密度を温度の関数として表して上の式と比
べればよい.物質成分のエネルギー密度を担う粒子の数が変わらない限り,物
質のエネルギー密度はスケール因子の3乗に反比例する.このことと,エント
ロピー保存による式(4.1.20)によれば,
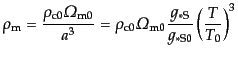 |
(D.2.25) |
となる.輻射成分と物質成分のエネルギー密度がちょうど等しくなる等密度時
の温度
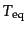 は式(4.2.24)と式(4.2.25)を等しく置くこ
とで求められる.さらにまたその時期のスケール因子
は式(4.2.24)と式(4.2.25)を等しく置くこ
とで求められる.さらにまたその時期のスケール因子
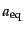 と赤方
偏移
と赤方
偏移
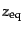 も求まる.有効自由度が現在値に固定した後にある解を探す
ことにより容易に,
も求まる.有効自由度が現在値に固定した後にある解を探す
ことにより容易に,
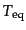 |
 |
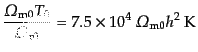 |
(D.2.26) |
 |
 |
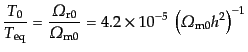 |
(D.2.27) |
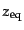 |
 |
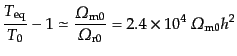 |
(D.2.28) |
と求まる.実際に宇宙における有効自由度は電子が非相対論的になっている温
度
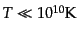 において固定しているが,実際に上で見つけた解
はこれを満たしている.
において固定しているが,実際に上で見つけた解
はこれを満たしている.
曲率や宇宙定数の効かない初期でのハッブルパラメータのふるまいは,有効自
由度が固定した時期以後,スケール因子の関数として
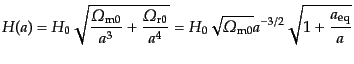 |
(D.2.29) |
で与えられる.有効自由度が固定するまでは上式には補正が必要だが,そこま
での時間は等密度時の時間に比べれば無視し得る.したがって,等密度時
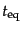 は
は
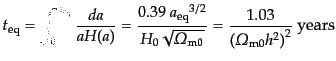 |
(D.2.30) |
である.
また,有用な関係として,輻射優勢期における温度と時間の関係を導いておこ
う.すでに述べたように,輻射優勢期にはフリードマン方程式において曲率と
宇宙定数の効果は無視でき,
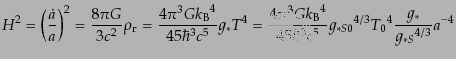 |
(D.2.31) |
となる.ここで,
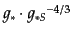 の時間変化は
の時間変化は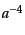 の時間変
化に比べればずっと小さいので近似的にこれを一定とすれば,上式の積分より
の時間変
化に比べればずっと小さいので近似的にこれを一定とすれば,上式の積分より
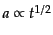 となる.すると,
となる.すると, となるから再び上式により
となるから再び上式により
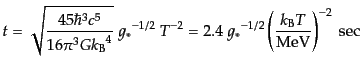 |
(D.2.32) |
すなわち,おおまかに言って輻射優勢期における時間は温度の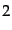 乗に反比例
し,時刻が1秒のとき宇宙はほぼ
乗に反比例
し,時刻が1秒のとき宇宙はほぼ
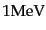 に対応する温度になっている.
に対応する温度になっている.





次へ: ガモフの基準と脱結合
上へ: ビッグバン宇宙モデル
前へ: 初期宇宙の熱力学
目次
索引
All rights reserved © T.Matsubara 2004-2010
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11