




次へ: 距離 - 赤方偏移関係
上へ: フリードマン・ルメートルモデル
前へ: エネルギー成分
目次
索引
Subsections
スケール因子のふるまいを簡単な場合から順に調べていく.
まず,輻射優勢期で等密度時より十分以前
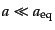 を考える.こ
のとき,フリードマン方程式(3.3.40)は
を考える.こ
のとき,フリードマン方程式(3.3.40)は
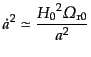 |
(C.4.42) |
となるので,直ちに解
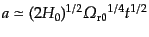 |
(C.4.43) |
を得る.つまり,時間の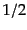 乗に比例してスケール因子が成長する.
乗に比例してスケール因子が成長する.
次に,物質優勢期で等密度時より十分後,
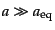 を考える.この
ときには,フリードマン方程式は
を考える.この
ときには,フリードマン方程式は
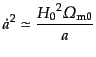 |
(C.4.44) |
であるから,解は,
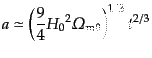 |
(C.4.45) |
となる.輻射優勢期よりも成長スピードが上がり,時間の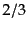 乗に比例して
成長するようになる.
乗に比例して
成長するようになる.
宇宙定数がゼロで,曲率優勢期に入った未来の宇宙のふるまいを考える.曲率
優勢となる条件
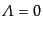 ,
, 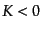 ,
,
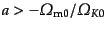 におけるフリードマン方程式は
におけるフリードマン方程式は
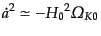 |
(C.4.46) |
であるから,解は,
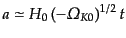 |
(C.4.47) |
となって,時間について線形的に成長する.この宇宙を ミルン宇宙
(Milne universe)と呼ぶ.
次に,宇宙定数が正で,真空エネルギー優勢期に入った宇宙のふるまいを考え
る.真空エネルギー優勢となる条件
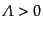 ,
,
![$ a > \max [({\mit\Omega}_{\rm m0}/{\mit\Omega}_{{\mit\Lambda}
0})^{1/3}, ({\mit\Omega}_{\rm K0}/\vert{\mit\Omega}_{\Lambda 0}\vert)^{1/2}]$](img335.png) におけるフリードマン方程式は
におけるフリードマン方程式は
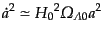 |
(C.4.48) |
であるから,解は,
![$\displaystyle a \simeq C \exp\left[({\mit\Omega}_{{\mit\Lambda}0})^{1/2} H_0 t\right] = C \exp\left[\left(\frac{{\mit\Lambda}}{3}\right)^{1/2} ct \right]$](img348.png) |
(C.4.49) |
となる.ここで,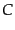 は定数であり,真空エネルギー優勢期に入る前までのス
ケール因子の成長による量である.この宇宙をドジッター宇宙 (de Sitter universe)と呼ぶ.これは指数関数的な凄まじい成長をする.
は定数であり,真空エネルギー優勢期に入る前までのス
ケール因子の成長による量である.この宇宙をドジッター宇宙 (de Sitter universe)と呼ぶ.これは指数関数的な凄まじい成長をする.
フリードマンモデルとは,宇宙定数をゼロとした宇宙モデルである.ここでは
物質優勢期以後を考えることにして,
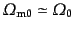 を用いる.このモデルでは,式(3.2.27)によって,物質の
密度と曲率には一対一の関係がつき,
を用いる.このモデルでは,式(3.2.27)によって,物質の
密度と曲率には一対一の関係がつき,
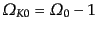 となる
ことから,
となる
ことから,
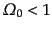 のとき曲率が負の開いた宇宙,逆に
のとき曲率が負の開いた宇宙,逆に
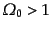 のとき曲率が正の閉じた宇宙となる.フリードマン方程式は
のとき曲率が正の閉じた宇宙となる.フリードマン方程式は
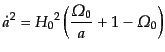 |
(C.4.50) |
となる.これは積分形では,
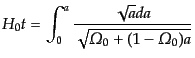 |
(C.4.51) |
という形となり,初等的に積分することが可能である.その結果として,
-
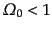 (
(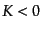 )のとき
)のとき
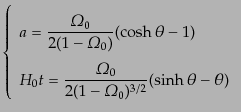 |
(C.4.52) |
-
 (
(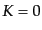 )のとき
)のとき
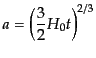 |
(C.4.53) |
-
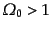 (
(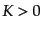 )のとき
)のとき
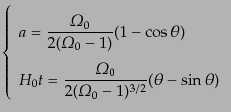 |
(C.4.54) |
のようになる.このスケール因子の解のふるまいは図3.1のようにな
る.
図 3.1:
フリードマンモデルのスケール因子のふるまい
|
|
ここで特に
 (
(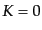 )の場合の宇宙は曲率も
宇宙定数もない特に簡単な宇宙であり,アインシュタイン・ドジッター
宇宙 (Einstein-de Sitter universe)と呼ばれる.この宇宙の密度は
臨界密度に等しく,スケール因子は時間の
)の場合の宇宙は曲率も
宇宙定数もない特に簡単な宇宙であり,アインシュタイン・ドジッター
宇宙 (Einstein-de Sitter universe)と呼ばれる.この宇宙の密度は
臨界密度に等しく,スケール因子は時間の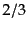 乗に比例して,ベキ的な簡単
な成長をする.曲率や宇宙定数のある一般の宇宙でも,宇宙初期にはアインシュ
タイン・ドジッター宇宙と同じようなふるまいをしていた[式(3.4.45)].
実際,式(3.4.52), (3.4.54)の
乗に比例して,ベキ的な簡単
な成長をする.曲率や宇宙定数のある一般の宇宙でも,宇宙初期にはアインシュ
タイン・ドジッター宇宙と同じようなふるまいをしていた[式(3.4.45)].
実際,式(3.4.52), (3.4.54)の
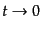 の極限をとれ
ば,
の極限をとれ
ば,
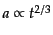 となっている.
となっている.
いずれの場合も,宇宙はスケール因子がゼロから始まる解となることに注意し
よう.すぐ下でみるように,宇宙定数のある場合でも,例外的な場合を除いて
同様の性質が現れる.スケール因子がゼロの点では密度は無限大に発散してし
まい,宇宙は特異点から始まったことになる.この特異点から以前にはもはや
時間を遡ることはできない.我々の知っている物理法則,とくに一般相対論が
破綻してしまうのである.この特異点は宇宙の一様等方性というきつい制限か
ら来た非物理的なものではないかと考えられるかもしれないが,残念ながら非
一様な宇宙であっても,時空が一般相対論に従う限り,かなり一般的な条件の
もとでこの特異点は避けられないということが明らかになっている(特異点定
理).この特異点はビッグバンと呼ばれ,どのような理由でビッグバンが始め
られたのかはいまだ明らかではない.ところが,後に見て行くように,このよ
うなビッグバンによって宇宙が始まったという観測的な証拠が驚くべきことに
数多く存在するのである.
密度が臨界密度に等しいか,小さい場合は,宇宙は永遠に膨張し続ける.これ
は物質の量が少ないために,すでに膨張運動している宇宙を重力的に引き留め
られず,際限なく宇宙が広がり続けてしまうことを意味する.逆に密度が臨界
密度より大きい場合はいったん膨張が止まり,収縮へ向かう宇宙となる.これ
は物質の十分な重力によって,膨張運動を引き留めることができるに対応して
いる.このとき,膨張の止まる時点をビッグストップといい,収縮により宇宙
が再び潰れてしまう時点をビッグクランチということがある.
次に,宇宙定数はあるが,曲率のない場合を考える.ふたたび物質優勢期以後
を考えることにして,
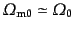 を用いると,この
場合には,
を用いると,この
場合には,
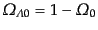 が成り立つ.フリー
ドマン方程式は
が成り立つ.フリー
ドマン方程式は
![$\displaystyle \dot{a}^2 = {H_0}^2 \left[\frac{{\mit\Omega}_0}{a} + (1 - {\mit\Omega}_0) a^2 \right]$](img364.png) |
(C.4.55) |
となるので,その積分形は
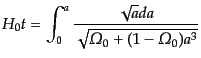 |
(C.4.56) |
である.これも容易に積分でき,その結果は
-
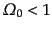 (
(
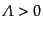 )のとき
)のとき
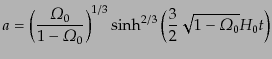 |
(C.4.57) |
-
 (
(
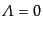 )のとき
)のとき
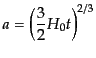 |
(C.4.58) |
-
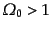 (
(
 )のとき
)のとき
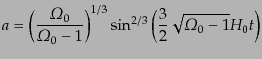 |
(C.4.59) |
となる.このスケール因子の解のふるまいは図3.2のようになる.
この場合も初期の特異点が必ず現れ,ビッグバンから始まる宇宙とな
る.物質の密度が小さく正の宇宙定数を持つ場合,はじめは減速しているが,
ある時点から加速しはじめ,その後は際限のない指数関数的膨張をするドジッ
ター宇宙へ近付いていく.一方,物質の密度が大きく,負の宇宙定数を持つ場
合には再収縮宇宙となる.
フリードマン方程式の一般の場合の解は解析的に求まらないこともないが,楕
円関数による複雑な表式となるので,あまり有用ではない.だが,定性的な解
のふるまいは以下に見るように比較的明らかである.そのためには,フリード
マン方程式を次の形に書き換えてみる:
| |
|
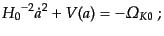 |
(C.4.60) |
| |
|
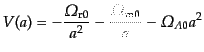 |
(C.4.61) |
すると,この式はポテンシャル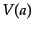 中にある質量
中にある質量
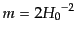 , エネ
ルギー
, エネ
ルギー
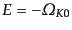 の質点の運動を記述するエネルギー方程式
の質点の運動を記述するエネルギー方程式
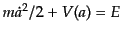 に等しい.したがって,ポテンシャル
に等しい.したがって,ポテンシャル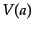 の形か
ら,スケール因子のふるまいは容易に想像できる.輻射成分,物質成分ともに
密度パラメータは正であるから,このポテンシャルは
の形か
ら,スケール因子のふるまいは容易に想像できる.輻射成分,物質成分ともに
密度パラメータは正であるから,このポテンシャルは
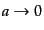 のとき
はいつでも負の方向へ発散する.だが,スケール因子の大きいところでのふる
まいは宇宙定数の符号によって大きく異なることになる.
のとき
はいつでも負の方向へ発散する.だが,スケール因子の大きいところでのふる
まいは宇宙定数の符号によって大きく異なることになる.
宇宙定数がゼロの場合はフリードマンモデルであり,ここでは考えない.
宇宙定数が負の場合は
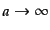 で正に発散していて,ポテンシャ
ルは単調増加することになる(図3.3).
で正に発散していて,ポテンシャ
ルは単調増加することになる(図3.3).
したがって,エネルギー項に対応する曲率の値にかかわらず,ビッグバン
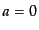 から始まったスケール因子はいずれポテンシャルの壁にぶつかって,跳
ね返って戻ってくる.これは必ず再収縮宇宙となることを意味する.
から始まったスケール因子はいずれポテンシャルの壁にぶつかって,跳
ね返って戻ってくる.これは必ず再収縮宇宙となることを意味する.
次に宇宙定数が正の場合には,
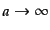 で負に発散していて,
ポテンシャルは極大点を持つことになる(図3.4).
で負に発散していて,
ポテンシャルは極大点を持つことになる(図3.4).
この場合には,曲率の値,初期条件によって,いくつか定性的に異なるふるま
いをする.物質優勢期以後を考えるとすると,ポテンシャルの極大点の位置は
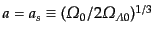 にあり,そのポ
テンシャルの値は
にあり,そのポ
テンシャルの値は
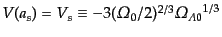 である.そこで,次の3つの場合に分けて考
えられる:
である.そこで,次の3つの場合に分けて考
えられる:
-
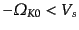 の場合:
の場合:
このときはスケール因子がどちらかの方
向へ跳ね返ることになる.現在値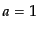 が極大点よりも小さい
が極大点よりも小さい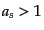 の場合
には図のAに対応して,再収縮宇宙となる.逆に
の場合
には図のAに対応して,再収縮宇宙となる.逆に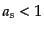 ならば図のBに対応
して,大きいスケール因子から収縮してきて有限の
ならば図のBに対応
して,大きいスケール因子から収縮してきて有限の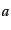 で跳ね返り,最終的に
はまた膨張してドジッター宇宙へ近付いていくようなものとなる.この後者の
宇宙には特異点が現れず,ビッグバンのない宇宙モデルとなっている.
で跳ね返り,最終的に
はまた膨張してドジッター宇宙へ近付いていくようなものとなる.この後者の
宇宙には特異点が現れず,ビッグバンのない宇宙モデルとなっている.
-
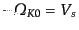 の場合:
の場合:
この場合も極大点の位置により異なるふ
るまいをする.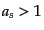 であれば図のCに対応して,減速しながら膨張するが
有限の
であれば図のCに対応して,減速しながら膨張するが
有限の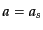 に近付き続けるような宇宙となる.時間が無限にすぎた極限
を考えると,宇宙は静止している状態に落ち着くことになる.これはアインシュ
タインがはじめて一般相対論に基づいて静止宇宙モデルを作ったときのモデル
に等価であり,アインシュタインの定常解と呼ばれる.この解はポテンシャル
の頂上に止まっているようなものなので,不安定な解であることがわかる.逆
に,
に近付き続けるような宇宙となる.時間が無限にすぎた極限
を考えると,宇宙は静止している状態に落ち着くことになる.これはアインシュ
タインがはじめて一般相対論に基づいて静止宇宙モデルを作ったときのモデル
に等価であり,アインシュタインの定常解と呼ばれる.この解はポテンシャル
の頂上に止まっているようなものなので,不安定な解であることがわかる.逆
に,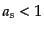 であれば図のDに対応して,
であれば図のDに対応して,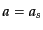 からゆっくり出発し,そ
のうち加速膨張する宇宙となる.この最後の場合は定常状態から出発するとす
ればビッグバンのないモデルである.これらのふるまいの時間をちょうど逆に
した解もあるが,膨張期を持たないので,現実の宇宙には対応しない.
からゆっくり出発し,そ
のうち加速膨張する宇宙となる.この最後の場合は定常状態から出発するとす
ればビッグバンのないモデルである.これらのふるまいの時間をちょうど逆に
した解もあるが,膨張期を持たないので,現実の宇宙には対応しない.
-
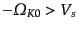 の場合:
の場合:
この場合ははじめ減速膨張しているが,
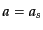 を境にして加速膨張に転じ,その後は際限なく膨張するドジッター
宇宙へ近付いて行く.図のEに対応する.
を境にして加速膨張に転じ,その後は際限なく膨張するドジッター
宇宙へ近付いて行く.図のEに対応する.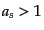 なら現在減速膨張のフェー
ズにあり,
なら現在減速膨張のフェー
ズにあり,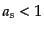 なら現在加速膨張のフェーズにある.
なら現在加速膨張のフェーズにある.
以上の大局的なふるまいを宇宙パラメータの値によってまとめて図に表すと,
図3.5のようになる.
図 3.5:
宇宙の大局的なふるまいと宇宙パラメータ
|
|





次へ: 距離 - 赤方偏移関係
上へ: フリードマン・ルメートルモデル
前へ: エネルギー成分
目次
索引
All rights reserved © T.Matsubara 2004-2010
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11
![]() を考える.こ
のとき,フリードマン方程式(3.3.40)は
を考える.こ
のとき,フリードマン方程式(3.3.40)は
![]() を考える.この
ときには,フリードマン方程式は
を考える.この
ときには,フリードマン方程式は
![]() ,
, ![]() ,
,
![]() におけるフリードマン方程式は
におけるフリードマン方程式は
![]() ,
,
![]() におけるフリードマン方程式は
におけるフリードマン方程式は
![]() を用いる.このモデルでは,式(3.2.27)によって,物質の
密度と曲率には一対一の関係がつき,
を用いる.このモデルでは,式(3.2.27)によって,物質の
密度と曲率には一対一の関係がつき,
![]() となる
ことから,
となる
ことから,
![]() のとき曲率が負の開いた宇宙,逆に
のとき曲率が負の開いた宇宙,逆に
![]() のとき曲率が正の閉じた宇宙となる.フリードマン方程式は
のとき曲率が正の閉じた宇宙となる.フリードマン方程式は
![]() を用いると,この
場合には,
を用いると,この
場合には,
![]() が成り立つ.フリー
ドマン方程式は
が成り立つ.フリー
ドマン方程式は
![]() で正に発散していて,ポテンシャ
ルは単調増加することになる(図3.3).
で正に発散していて,ポテンシャ
ルは単調増加することになる(図3.3).
![]() で負に発散していて,
ポテンシャルは極大点を持つことになる(図3.4).
で負に発散していて,
ポテンシャルは極大点を持つことになる(図3.4).
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11