




次へ: 見かけのサイズ
上へ: ロバートソン・ウォーカー計量
前へ: 見かけの明るさ
目次
索引
ハッブル則は,銀河の後退速度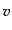 と天体までの距離
と天体までの距離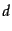 についての関係式
についての関係式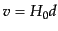 で与えられた.ここで,後退速度と言っているものは赤方偏移を非相対
論的後退速度によるドップラー効果と解釈した場合のものであり,観測量とし
ては赤方偏移に光速をかけた
で与えられた.ここで,後退速度と言っているものは赤方偏移を非相対
論的後退速度によるドップラー効果と解釈した場合のものであり,観測量とし
ては赤方偏移に光速をかけた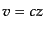 で実際には与えられるものである.また,
距離
で実際には与えられるものである.また,
距離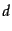 は絶対光度の推定のもとに見かけの光度を用いて見積もったものであ
るから,光度距離
は絶対光度の推定のもとに見かけの光度を用いて見積もったものであ
るから,光度距離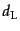 に他ならない.また,ハッブル則は赤方偏移の
小さな
に他ならない.また,ハッブル則は赤方偏移の
小さな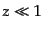 の観測によって求められたものである.したがって,ハッブル
則は
の観測によって求められたものである.したがって,ハッブル
則は
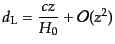 |
(B.6.50) |
と表すことができる.
これをRW計量のもとで導いてみよう.そのためには,式(2.5.40)を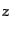 でテイラー展開すればよい.そのためにまず,スケール因子
でテイラー展開すればよい.そのためにまず,スケール因子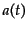 を現在時刻
を現在時刻
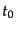 のまわりでテイラー展開する:
のまわりでテイラー展開する:
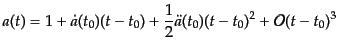 |
(B.6.51) |
ここで,ドットは時間微分を表す.すると,赤方偏移の展開は,
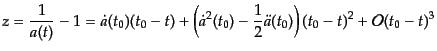 |
(B.6.52) |
である.一方,座標距離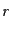 の展開は式(2.4.26)より求められ,2次ま
ででは曲率
の展開は式(2.4.26)より求められ,2次ま
ででは曲率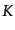 によらず,
によらず,
![$\displaystyle r = c\left[t_0 - t + \frac12 \dot{a}(t_0) (t_0 - t)^2 + {\cal O}(t-t_0)^3\right]$](img200.png) |
(B.6.53) |
となる.したがって,式(2.5.40), (2.6.52), (2.6.53)を
使えば光度距離を赤方偏移で展開した式が得られる:
![$\displaystyle d_{\rm L} = \frac{c}{\dot{a}(t_0)} \left[ z + \frac12 \left(1 + \frac{\ddot{a}(t_0)}{\dot{a}^2(t_0)}\right) z^2 + {\cal O}(z^3) \right]$](img201.png) |
(B.6.54) |
これを式(2.6.50)と比べれば,ハッブル定数はRW計量においてスケール
因子の時間微分
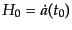 |
(B.6.55) |
であることがわかる.また,赤方偏移の2次の項の存在は赤方偏移の大きいと
ころでハッブル則が線形からずれることを示している.減速パラメータ
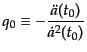 |
(B.6.56) |
を導入すれば,線形関係からの2次の補正が特徴づけられる.すなわち,光度
距離の展開は,
![$\displaystyle d_{\rm L} = \frac{c}{H_0} \left[ z + \frac12 (1 - q_0) z^2 + {\cal O}(z^3) \right]$](img204.png) |
(B.6.57) |
と書ける.





次へ: 見かけのサイズ
上へ: ロバートソン・ウォーカー計量
前へ: 見かけの明るさ
目次
索引
All rights reserved © T.Matsubara 2004-2010
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11
![]() と天体までの距離
と天体までの距離![]() についての関係式
についての関係式![]() で与えられた.ここで,後退速度と言っているものは赤方偏移を非相対
論的後退速度によるドップラー効果と解釈した場合のものであり,観測量とし
ては赤方偏移に光速をかけた
で与えられた.ここで,後退速度と言っているものは赤方偏移を非相対
論的後退速度によるドップラー効果と解釈した場合のものであり,観測量とし
ては赤方偏移に光速をかけた![]() で実際には与えられるものである.また,
距離
で実際には与えられるものである.また,
距離![]() は絶対光度の推定のもとに見かけの光度を用いて見積もったものであ
るから,光度距離
は絶対光度の推定のもとに見かけの光度を用いて見積もったものであ
るから,光度距離![]() に他ならない.また,ハッブル則は赤方偏移の
小さな
に他ならない.また,ハッブル則は赤方偏移の
小さな![]() の観測によって求められたものである.したがって,ハッブル
則は
の観測によって求められたものである.したがって,ハッブル
則は
![]() でテイラー展開すればよい.そのためにまず,スケール因子
でテイラー展開すればよい.そのためにまず,スケール因子![]() を現在時刻
を現在時刻
![]() のまわりでテイラー展開する:
のまわりでテイラー展開する:
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11