




次へ: ハッブル図
上へ: ロバートソン・ウォーカー計量
前へ: 赤方偏移
目次
索引
光の伝播の途中で吸収がない理想的な場合,天体そのものの光度
(luminosity)  と我々が観測する見かけの天体の明るさ
と我々が観測する見かけの天体の明るさ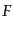 は比例する.こ
こで,
は比例する.こ
こで, は天体の静止系において単位時間あたりに放出される全エネルギー
であり,
は天体の静止系において単位時間あたりに放出される全エネルギー
であり,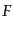 は単位面積,単位時間あたりに観測者が受けるエネルギーであり,
これを観測者の位置でのフラックス (flux) という.静止ユークリッド空間で
の関係は
は単位面積,単位時間あたりに観測者が受けるエネルギーであり,
これを観測者の位置でのフラックス (flux) という.静止ユークリッド空間で
の関係は
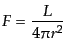 |
(B.5.30) |
であるが,RW計量では膨張と曲率の効果により,この関係は変更を受ける.
まず,赤方偏移によって光のエネルギーが小さくなる.そこで,光源において
波長範囲
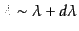 の中に放出されるエネルギーを
の中に放出されるエネルギーを
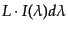 とする.ここで,
とする.ここで, は全放出エネルギーであ
り,
は全放出エネルギーであ
り,
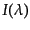 はエネルギー分布を表す関数で,規格化
はエネルギー分布を表す関数で,規格化
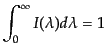 |
(B.5.31) |
を持つ.光源から,波長範囲
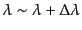 ,時間
範囲
,時間
範囲
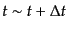 の間に放出されるエネルギーは
の間に放出されるエネルギーは
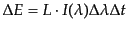 |
(B.5.32) |
である.1光子あたりのエネルギーは
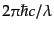 であるから,その
光子数は
であるから,その
光子数は
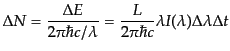 |
(B.5.33) |
である.ここで,対応する光を観測者が観測するときの波長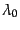 ,時
間間隔
,時
間間隔
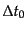 は赤方偏移によって,
は赤方偏移によって,
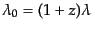 ,
,
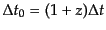 となるので,式(2.5.33)は
となるので,式(2.5.33)は
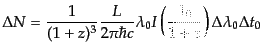 |
(B.5.34) |
と表される.光源からRW計量の座標距離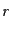 にある球面の面積は
にある球面の面積は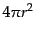 で
ある(そうなるように座標距離が定義された).したがって,観測者が単位面積,
単位時間あたりに受けるエネルギーは
で
ある(そうなるように座標距離が定義された).したがって,観測者が単位面積,
単位時間あたりに受けるエネルギーは
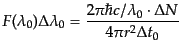 |
(B.5.35) |
であるから,観測者の位置でのフラックスは,
![$\displaystyle F(\lambda_0) = \frac{L\cdot I\left[\lambda_0/(1+z)\right]}{4\pi r^2 (1+z)^3}$](img169.png) |
(B.5.36) |
である.
放射の全エネルギーを測る抵抗熱量計のことをボロメータ (bolometer) とい
う.ボロメータによって測定したエネルギーは全波長で積分したフラックスに
対応するので,これをボロメトリックフラックス (bolometric flux)と言い,
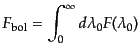 |
(B.5.37) |
で与えられる.また,天体から放出される全エネルギーはボロメトリック光度
に対応し,
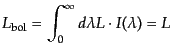 |
(B.5.38) |
である.したがって,これらの関係はよりシンプルに,
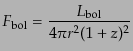 |
(B.5.39) |
となる.このボロメトリックな量を用いて,あたかも静止ユークリッド空間で
あるかのように天体までの距離を見積もったものを,光度距離(luminosity distance) 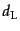 という:
という:
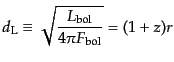 |
(B.5.40) |
さて,フラックスを対数スケールで表したものは伝統的な等級 (magnitude)
である.ボロメトリックな見かけの等級は
 |
(B.5.41) |
で与えられるB1.ここで,
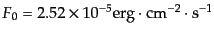 |
(B.5.42) |
は等級がゼロに対応するフラックスである.また,ある天体が10pcの距離にあっ
たとしたときの見かけの等級は絶対等級と呼び,ボロメトリックの場合
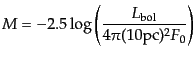 |
(B.5.43) |
で与えられる.これらの等級を用いれば,光度距離は
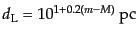 |
(B.5.44) |
となる.したがって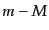 は光度距離と一対一の関係にあるため,これを
距離指数 (distance modulus) と呼び,以下のような式で与えられる:
は光度距離と一対一の関係にあるため,これを
距離指数 (distance modulus) と呼び,以下のような式で与えられる:
全光度を測定しない,あるいはできない場合は波長の範囲を限定した観測とな
り,上のようなシンプルな式には補正が必要である.これをK-補正
(K-correction)と呼ぶ.あるバンドBandに限定した観測を行うことを
考えてみる.このときのフラックスは
![$\displaystyle F_{\rm Band} = \int_{\rm Band} F(\lambda_0) d\lambda_0 = \frac{L\int_{\rm Band} I[\lambda_0/(1+z)] d\lambda_0} {4\pi r^2 (1 + z)^3}$](img187.png) |
(B.5.46) |
で与えられる.この天体が10pcにあるとしたときのフラックスは
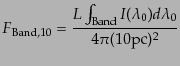 |
(B.5.47) |
であるから,このバンドでの距離指数は,
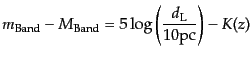 |
(B.5.48) |
となる.ここで,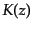 がK-補正であり,
がK-補正であり,
![$\displaystyle K(z) = 2.5 \log \left(\frac{\int_{\rm Band} I[\lambda_0/(1+z)] d\lambda_0/(1+z)} {\int_{\rm Band} I(\lambda_0) d\lambda_0} \right)$](img191.png) |
(B.5.49) |
で与えられる.これは天体のスペクトル分布
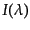 を知ることにより計
算できる.
を知ることにより計
算できる.
Footnotes
- ...
で与えられるB1
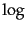 は10の対数
は10の対数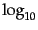 である.
である.





次へ: ハッブル図
上へ: ロバートソン・ウォーカー計量
前へ: 赤方偏移
目次
索引
All rights reserved © T.Matsubara 2004-2010
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11
![]() と我々が観測する見かけの天体の明るさ
と我々が観測する見かけの天体の明るさ![]() は比例する.こ
こで,
は比例する.こ
こで,![]() は天体の静止系において単位時間あたりに放出される全エネルギー
であり,
は天体の静止系において単位時間あたりに放出される全エネルギー
であり,![]() は単位面積,単位時間あたりに観測者が受けるエネルギーであり,
これを観測者の位置でのフラックス (flux) という.静止ユークリッド空間で
の関係は
は単位面積,単位時間あたりに観測者が受けるエネルギーであり,
これを観測者の位置でのフラックス (flux) という.静止ユークリッド空間で
の関係は
![]() の中に放出されるエネルギーを
の中に放出されるエネルギーを
![]() とする.ここで,
とする.ここで,![]() は全放出エネルギーであ
り,
は全放出エネルギーであ
り,
![]() はエネルギー分布を表す関数で,規格化
はエネルギー分布を表す関数で,規格化
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11