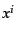 (
(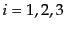 ), 3次元
超面ごとに時間座標
), 3次元
超面ごとに時間座標  (
(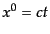 ) を張ることができ,これは時空を記
述する座標系として,
) を張ることができ,これは時空を記
述する座標系として,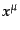 (
(
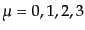 ) を構成する.ここで交差す
る世界線があると1点に2つの
) を構成する.ここで交差す
る世界線があると1点に2つの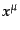 の値が対応してしまってこのような座標
は張ることができなくなるため,ワイルの要請が本質的である.
の値が対応してしまってこのような座標
は張ることができなくなるため,ワイルの要請が本質的である.
宇宙の時空のふるまいは一般相対論によって調べられるが,これを現実的に行 うためには宇宙そのものに時間座標と空間座標を張れることが不可欠である. だが,実際の宇宙では粒子の世界線が互いに交差し合い,相対論によれば異な る粒子に沿って測った時間は異なる時間を与える.このように現実の宇宙には 厳密な意味での宇宙の時間座標を定義することができない.だが,そのような 世界線の交差は宇宙全体から見れば小さなスケールで起こっていることである. 具体的には銀河のスケールでの衝突はあるが,銀河団,超銀河団のスケールで は衝突はほとんどないものと考えられている.ひとまず宇宙の構造を無視して, 宇宙全体の振る舞いを調べようというときには物質の世界線の交差は無視して 取り扱っても不都合はないと考えられる.そこで,次の仮定を要請する:
これをワイルの要請と呼ぶ.ただし,後に明らかになるように,宇宙の初期に は密度が無限大になる特異点が予想されるが,その点ではすべての世界線が一 点に集約する.このような初期の特異点のみは上の要請の例外とする.
ワイルの要請のもとでは物質素片ごとに空間座標 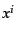 (
(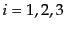 ), 3次元
超面ごとに時間座標
), 3次元
超面ごとに時間座標  (
(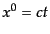 ) を張ることができ,これは時空を記
述する座標系として,
) を張ることができ,これは時空を記
述する座標系として,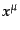 (
(
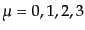 ) を構成する.ここで交差す
る世界線があると1点に2つの
) を構成する.ここで交差す
る世界線があると1点に2つの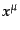 の値が対応してしまってこのような座標
は張ることができなくなるため,ワイルの要請が本質的である.
の値が対応してしまってこのような座標
は張ることができなくなるため,ワイルの要請が本質的である.
このときにワイルの要請を満たす宇宙の計量を求めよう.まず,測地線の接ベ
クトル
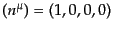 と3次元超面上の任意の接ベクトル
と3次元超面上の任意の接ベクトル
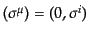 が垂直になることから,
が垂直になることから,
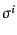 は任意なので,結局
は任意なので,結局
座標値一定
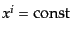 の点が測地線をなす座標では,測地線
方程式
の点が測地線をなす座標では,測地線
方程式
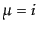 成分は
成分は
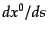 は時間座標と物質素片の固有時間との比であるか
らゼロにはならず,結局
は時間座標と物質素片の固有時間との比であるか
らゼロにはならず,結局
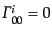 である.クリストッフェル記号
は
である.クリストッフェル記号
は
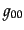 は
は のみの関数であることがわかる.し
たがって,
のみの関数であることがわかる.し
たがって, を
を
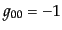 とすることができる.
とすることができる.
まとめると,ワイルの要請を満たす計量として次の形となる座標がつねにとれる
ことになる:
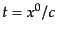 を宇宙時間(cosmic time)と呼ぶ.これが物質素片の固有
時間となっていることは,式(2.1.10)で
を宇宙時間(cosmic time)と呼ぶ.これが物質素片の固有
時間となっていることは,式(2.1.10)で
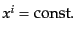 の世界
線を考えれば明らかであろう.また,ワイルの要請における3次元超面は宇宙
時間一定の面である.
の世界
線を考えれば明らかであろう.また,ワイルの要請における3次元超面は宇宙
時間一定の面である.
 visitors,
visitors,  pageviews since 2007.5.11
pageviews since 2007.5.11